4228
Dynamic Multiband Shimming and EPI at 7T
Chan Hong Moon1, Julie W. Pan1, and Hoby P. Hetherington1
1Radiology, University of Pittsburgh, Pittsburgh, PA, United States
1Radiology, University of Pittsburgh, Pittsburgh, PA, United States
Synopsis
At 7T, increased field strength and limited gradient performance results in increased geometric distortions for echo planar imaging. Use of higher order shims and dynamic updating on a slice by slice basis can dramatically reduce the extent of these distortions. This work describes: 1) the theoretical basis for the extension of slice by slice dynamic shim updating for multi-band acquisitions; 2) demonstrates that higher order spherical harmonic shim systems can intrinsically achieve MB=2 imaging with no loss in in-plane homogeneity in comparison to slice by slice shimming (MB=1), and 3) these improvements are easily visualizable in EPI.
Introduction
For the human brain, optimizing the B0 shim corrections on a slice-by-slice basis (SBS) as opposed to a single global solution over the entire brain, is known to significantly improve B0 homogeneity [1]. However, regardless of hardware configuration used for shimming, the advantages of rapid multi-band (MB) imaging, (where multiple spatially disparate slices are excited simultaneously) has outweighed the gains in B0 homogeneity of slower SBS shimming with dynamic shim updating (DSU). Therefore, the goal of this work was to develop a theoretical framework for MB shimming (i.e. simultaneous optimization of multiple spatially discrete slices) and demonstrate its performance using the very high order shim (VHOS) insert with echo planar imaging (EPI) at 7T.Theory
For thin axial slices, spherical harmonic shims can be divided into two groups, i.e. those without a linear z-dependence (Cn,Sn,Z0,Z2,Z2Cn,Z2Sn…), denoted as “non-z-degenerate NzD” and with a linear z dependence “z-degenerate zD” (ZCn,ZSn,Z,Z3,Z3Cn,Z3Sn…) wherezDi(x,y) = b0*Z0 + b1*z * NzDi(x,y) [Eq. 1]
Since the zDi shims are numerically related to their NzDi, partners by a scaling parameter determined by their position along the Z axis, they provide no additional improvement in in-plane homogeneity for thin axial slices, such that the optimal shim is given by
B0(r) = B0(x,y,z) = a0*Z0 + Σai*NzDi(x,y) [Eq. 2]
Thus, DSU SBS shimming using only the NzD terms (i.e., ~ half of the available shims) should be largely identical to SBS DSU shimming using all (NzD and zD) of the available shims. However, combination of the zDi and NzDi shims allows for different and arbitrary sets of NzDi shim fields to be simultaneously generated at two disparate spatial locations, such that DSU MB=2 shimming of thin axial slices using NzDi and zDi shims should be able to achieve nearly identical results as DSU SBS (MB=1).
Methods
Data were acquired on a Siemens 7T system using an 8x2-channel transceiver array and a VHOS insert (Resonance Research, Inc., MA) providing 3rd, 4th and two 5th degree harmonic shims (ZC4 and ZS4). 1st and 2nd degree shims are provided by the Siemens gradient set. Each shim channel is dynamically updated for each slice (MB=1) or slice pair (MB=2) using 2ms ramp times. B0 maps were acquired with matrix size of 64x64x58 at 3x3x2 mm3 using 5 evolution times (0,1,2,4 and 8ms) [2].Shimming: The B0 data were acquired using 5 strategies: (1) 1st&2nd static global shimming; (2) 1st-4th static global shimming, (3) 1st-4th dynamic slice-by-slice (SBS DSU MB=1), (4) NzD only shims with dynamic SBS (i.e., using half of all available channels), and (5) 1st-4th DSU MB=2, using 8 subjects per group. The performance for higher MB factors (MB=3,4) was also simulated using the mapping data acquired from the NzD studies.
SMS MB EPI: To focus on issues of distortion, conventional (MB=1) and MB=2 spin echo (SE) EPI were acquired with 2mm isotropic resolution, GRAPPA acceleration in the PE direction (AF=3), 1408Hz/pixel with an echo spacing of 0.9ms. The SMS MB=2 EPI image was reconstructed using full 3D kx-ky-kz GRAPPA [3].
Analysis: The standard deviation (SD) of the B0 distribution per slice for the whole brain was measured. EPI images were compared to the B0 map and anatomy across the 3 acquisitions: 1st&2nd, 1st-4th static shimming vs. DSU MB=2 (Fig 3).
Results
Table 1 summarizes the experimentally achieved shim results, acquired with 8 subjects per group. DSU with 1st-4th order spherical harmonics reduces the inhomogeneity present by 53% and 40% in comparison to static global shimming with 2nd and 4th order shims respectively. Consistent with theory, MB=1 shimming using only the non-degenerate shims or MB=2 shimming or with all shims gave nearly identical results to that achieved with SBS (MB=1) shimming with all shims. Fig 1 displays B0 maps with MB=2 shimming. For the upper 40% of the brain (Fig 2), the residual inhomogeneity (<10Hz SD) is dominated by the intrinsic susceptibility difference between gray and white matter. Fig 3 show SE EPI data using the different shimming methods. As expected, DSU MB=2 EPI images were superior over entire brain in comparison data acquired with 1st&2nd static and 1st-4th static shimming. Predicted results from N=8 subjects for MB=3,4 are also provided (Table 1).Conclusions
When using DSU shimming with 1st-4th degree spherical harmonics, the residual B0 inhomogeneity over the upper 40% of the brain is largely limited by the intrinsic difference in susceptibility of gray and white matter. For more inferior brain locations substantial reductions in inhomogeneity are achieved which significantly reduce spatial distortions in EPI. Due to the intrinsic spatial symmetries for spherical harmonic shims, MB=2 shimming can be achieved without loss in homogeneity in comparison to SBS MB=1 shimming. Alternatively, for SBS (MB=1) shimming only ½ of the full set of harmonic shims are required to achieve optimal results, thereby simplifying hardware demands. At higher MB factors, (MB=3,4), the predicted improvement decreases, but still achieves 43% and 32% improvement respectively over 1st&2nd static global shimming. The developed MB DSU can significantly reduce in-plane geometric distortions at 7T for EPI acquisitions.Acknowledgements
The study is supported by NIH EB011639, EB009871, NS090417, NS081772.References
[1] Moon et al, ISMRM, #6653, 2018. [2] Hetherington et al, MRM, 56:26-33, 2006. [3] Moon et al, ISMRM, #2411, 2019.Figures

Table 1 B0 field inhomogeneity for static vs. DSU shimming
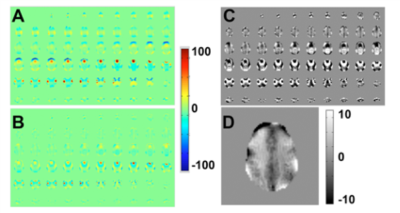
Figure 1 A: B0
maps, 58 2mm slices acquired using static 1st-4th+ shims,
sB0=21.3Hz;
B: B0 maps, 58 2mm slices acquired using 1st-4th+
dynamic MB=2 shimming, sB0=13.5Hz. C: DSU MB=2 maps, inverted scale +10Hz
for visualization. D: Single slice map with DSU MB=2 inverted scale +10Hz,
single slice sB0=4.5Hz.

Figure 2 Slice by slice SD of B0 field distribution
for 1st-2nd static, 1st-4th+ static
and 1st-4th+ DSU with MB=2.
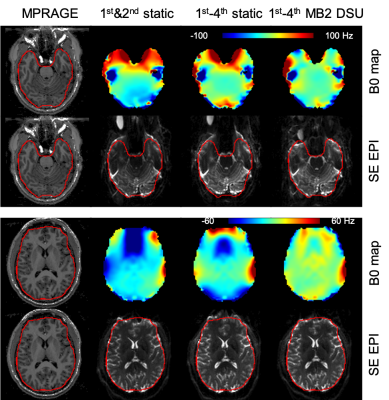
Figure 3 Comparison of B0 field map and SE EPI of
two representative slices acquired with 1st&2nd
static (2nd column panels), 1st-4th+ static (3rd
column) and 1st-4th SBS DSU MB=2 (4th column).
The red contour is the brain boundary calculated from the MP2RAGE images (1st
column).