Introduction

B₀ field inhomogeneity causes image artifacts and distortion in MRI¹. To reduce B₀ field inhomogeneity, spherical harmonics (SH) shimming is commonly used, however, it cannot perfectly resolve B0 field inhomogeneity especially in prefrontal cortex (PFC) and temporal lobe (TL). The multi-coil local shimming method, which utilizes multiple coils around the head to further improve the field homogeneity after SH shimming, has shown good performance². Recently, a few works showed that an optimized multi-coil geometry can improve shimming performance when compared to a hand-designed multi-coil shim of the same number of coils^3,4. In this work, we designed a multi-coil geometry using Bayesian optimization⁵, which is a powerful tool in finding the global minimum. The shimming performance of a machine-designed multi-coil local shim was compared with that of a hand-designed 48 channel multi-coil local shim^2,4.

Methods

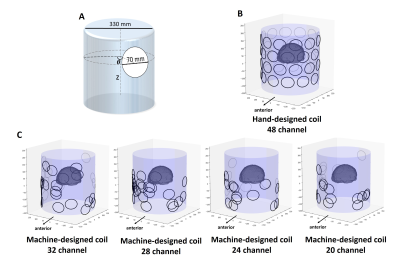
In this study, a multi-coil shim was designed with multiple 70 mm-diameter circular coils, which were placed on the surface of the cylinder of radius 330 mm. The position of each coil was parameterized by angular position (θ) and z-axis position (z) (Fig. 1a). The range of θ covered from -π to π (rad) and z covered from -140 to 175 (mm). Bayesian optimization was used to find an optimal multi-coil position. The limit of current in each coil was set to be 2 A assuming 25 turns for the coil⁴. The numbers of channels (or coils) for our design were 32 to 20 in the step size of 4 coils. The shimming performances of all the machine-designed shims were compared with a 48 channel hand-designed coil (Fig. 1b; the same 70 mm diameter). To evaluate the shimming performance, the field maps of 114 brains acquired at 3T were utilized. The field map was scanned using a 2D gradient-echo sequence. Detailed scan parameters are as follows: TE/TR = 7.38/425 ms, FA = 40°, FOV = 240×240×120 mm³, voxel size = 3×3×3 mm³. A local field was calculated from the phase image using Laplace unwrapping for phase unwrapping. The second-order SH shimming was applied digitally. The performance of each shim was assessed by calculating the mean of the root-mean-square (RMS) of each field map. To investigate the robustness of shimming performance for various head positioning, all the field maps modified by 8 different head position changes: ±20 mm of each axis and ±10° of rotation around the z-axis. For a statistical test, the shimming performance was compared between the hand-designed coil and machine-designed coil using a pairwise t-test with Bonferroni correction.

Results and Discussion

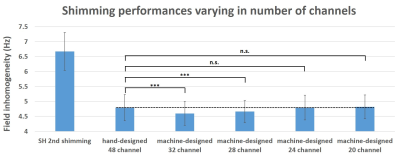
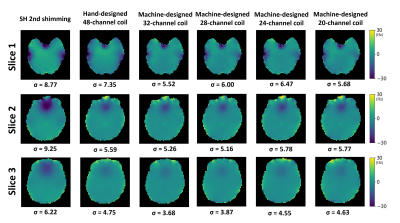
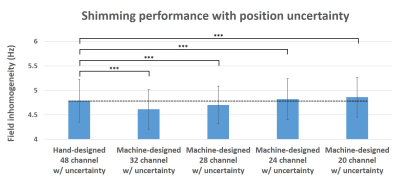
Figure 1b shows the hand-designed 48 channel multi-coil shim and Figure 1c shows the machine-designed multi-coil shim for 32, 28, 24, and 20 channels. As shown in Figure 1c, most of the coils in the machine-designed shim are located below PFC and TL, which have high inhomogeneity in the brain. These designs seem to generate fields that shim the highly inhomogenous regions. Figure 2 shows the performances of the machine-designed shims for the different numbers of the channel. Machine-designed 20 channel and 24 channel shims show comparable shimming performance to the hand-designed 48 channel multi-coil shim. Also, the machine-designed 28 channel and 32 channel shim outperform the hand-designed 48 channel shim. The representative field maps of the hand-designed multi-coil shim and machine-designed multi-coil shim results are shown in Figure 3. The inhomogeneity in the PFC and TL regions are effectively reduced in both coils. Figure 4 shows shimming performances for the position uncertainty (Fig. 4). In this test, the 32 channel and 28 channel shim still outperform the hand-designed coil. However, the 24 channel and 20 channel shim show degradation in performance.

Conclusion

In this work, we designed a multi-coil local shim using Bayesian optimization. The machine-designed multi-coil shim shows a comparable shimming ability to the hand-designed 48 channel shim setup for a smaller number of channels. Specifically, the machine-designed 28 channel shim outperforms the hand-designed 48 channel shim when evaluated with the positional uncertainty. To generate this geometry, the Bayesian optimization algorithm performed only 140 evaluations (less than 200 min). However, further investigation is necessary to check the optimality of the final design.

Acknowledgements

This work was supported by Samsung Research Funding & Incubation Center of Samsung Electronics under Project Number SRFC-IT1801-09 and by the Brain Korea 21 Plus Project in 2019