4225
Of stream functions and thin wires: An open-source tool for intuitive gradient coil design
Sebastian Littin1, Feng Jia1, and Maxim Zaitsev1
1Department of Radiology, Medical Physics, University of Freiburg, University Medical Center, Freiburg, Germany
1Department of Radiology, Medical Physics, University of Freiburg, University Medical Center, Freiburg, Germany
Synopsis
The design of gradient coils is sometimes perceived as complex. However, the relation between a current density and a stream function is a simple differentiation. Here we present an intuitive open source code collection to derive gradient coil designs from current densities. Stream functions are derived directly and indirectly from the current distribution. The aim of this work is to provide a simple tool for educational purposes. The code collection which is available on GitHub enables for straight-forward coil designs on simple surface geometries.
Introduction
The design of gradient coils is sometimes perceived as complex. However, the relation between a current density and a stream function is a simple differentiation. Here we present an intuitive open source code collection to derive gradient coil designs from current densities and stream functions on simple surface geometries. This collection yields for teaching and the wish to generate gradient coil designs with open source software. The complete collection includes the surface definition, the derivation of stream functions from current densities. Solvers to derive target fields from current densities stream functions, as well as plotting tools are included.Methods
A surface current density may be approximated by simple, infinitely small wires on the surface. For use in high main magnetic fields only the z-component, Bz, is usually considered in gradient coil design. For simple surface geometries thin wires oriented orthogonal to the z-axis sufficiently describe a current density. For each wire, m, the resulting magnetic field Bz at point n can be calculated using the Biot-Savart law. The resulting field may be expressed using a simple sensitivity matrix Snm, according to: Bz,n = Snm · Im.An inverse problem to get a current density for a given target field can be stated by deploying the pseudoinverse S+ of S in a least squares sense. However, this problem is ill-posed. Therefore a Tikhonov regularization may be used to find solutions with smaller norms, which effectively penalizes high opposing currents, acting to limit the total power.
The gradient of this current distribution may be used to display equally spaced iso-contours, usually denoted as stream function representation. Because the resulting stream lines derived from the current density might not be realizable as closed loops, an additional constraint may be added to ensure that the sum of currents along z is zero.
Another part of this code collection enables to derive a sensitivity matrix in the stream function domain. By combining neighboring thin wires along z, such that they carry the same current in opposite directions, a basic cell is formed from two neighboring wires. This can be simply done by combining two of the previously obtained sensitivity matrices Snm such that the same current flows in opposite directions within the same cell. The stream function may now be derived directly for a given target field.
Additionally included are plotting functions to display current distributions, stream functions and stream lines in 2D and 3D. The code was written in MATLAB (The MathWorks, Natick, MA, USA). However, the code runs in Octave, as well. The code is available on github:
Results
To demonstrate the code, indirect and direct stream functions which were derived from current distributions on a simple cylindrical surface are shown in the figure section. However, the code enables for the definition of multiple independent surfaces.Discussion
The motivation to share this code was to make a simple gradient coil design tool available which enables for the whole pipeline of coil design. Mainly for educational purposes. This includes the definition of the current carrying surface and the density of the individual discrete current elements. To the knowledge of the authors there are no gradient design tools which include all steps. Eg the code by Bringout et al. [1,2] does not include the surface definition.However the current implementation works only with simple, continuous surface geometries. Additionally, only the z-component of the magnetic field (Bz) is included. For other magnet geometries, such as Halbach arrays other components have to be considered. Only slight modifications are expected to extend the code for such purposes.
Except for the 3D plotting functions no problems could be observed while running it in Octave. The code is open source and available on GitHub [3]
Acknowledgements
Deutsche Forschungsgemeinschaft (DFG) - Project number za422/5-1 and za422/6-1References
[1] github.com/gBringout/CoilDesign
[2] G Bringout, IEEE Transactions on Magnetics 2015, 51(2): 5300604
[3] github.com/Sebastian-MR/GradStreamFigures

Figure 1: Each pixel represents a discrete thin-wire which is oriented orthogonal to z. The regularized current density depicted in a) may not be transformed to a coil design which is realizable with closed loops. The addition of a constraint, that the sum of currents along z equals 0 leads to a completely different current density as shown in b). The spatial derivative of this current density represents a stream function, shown in c). Iso-contours of such a stream function may be used to approximate the current density from b) by deploying discrete wires.
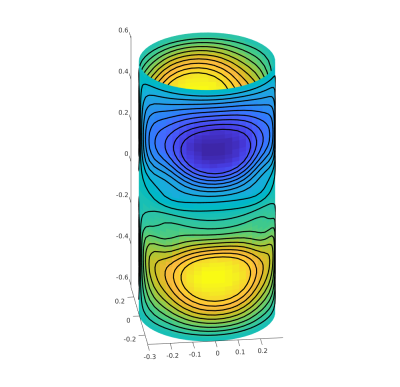
Figure 2: 3D representation of the stream function and iso-contours from Fig.1.
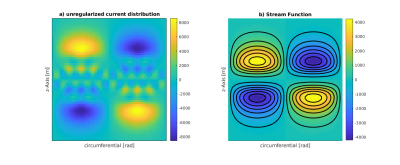
Figure 3: By combining neighboring thin-wires to one cell, a stream function basis may be formed. This enables to directly calculate the spatial derivative of the current density in the stream function domain. It can be seen from the unregularized stream function depicted in a) that this mathematical problem is ill-posed. A regularized design solved in the stream function domain is shown in b).
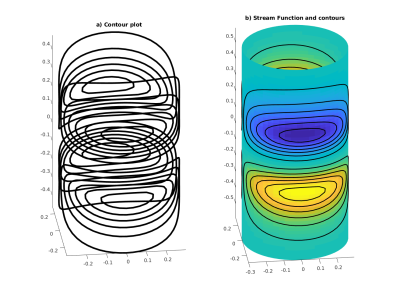
Figure 4: Depiction of iso-contours from the solution in the stream function domain a) and the combination of iso-contours and the stream function b) in a 3D representation