Introduction

Static field shimming of the human brain is essential for allowing artifact-less high-resolution 3D-acquisitions at Ultra-High Field. However, $$$\Delta{B_0}$$$ inhomogeneity becomes stronger as the main magnetic field $$$B_0$$$ increases. The mitigation of $$$B_z{\equiv}B_0$$$ tends to be more challenging at interfaces with air cavities in the head, which generate a susceptibility gradient in the brain. Here theoretical limits to brain shimming are explored.

Although increasing orders of Spherical Harmonics (SH) are proposed to zero-out this inhomogeneity, we show that, despite $$$\nabla^2B_z(\textbf{x})=0$$$ in the brain, SH-based fields have limited performance.

The solution to Laplace’s equation is¹: $$B_z(r,\theta,\phi) = \sum_{n=0}^{+\infty}\sum_{m=-n}^{n}{C_{n}^{m}\mathcal{R}_{n}^{m}(r,\theta,\phi)+D_{n}^{m}\mathcal{I}_{n}^{m}(r,\theta,\phi)}$$ with $$\mathcal{R}_{n}^{m}(r,\theta,\phi)=r^{n}Y_{n}^{m}(\theta,\phi)$$ $$\mathcal{I}_{n}^{m}(r,\theta,\phi)=\frac{1}{r^{n+1}}Y_{n}^{m}(\theta,\phi)$$ and $$$Y_{n}^{m}(\theta,\phi)$$$ a spherical harmonic of order $$$n$$$ and degree $$$m$$$. Any field shimming apparatus placed outside the region of interest (ROI), whatever its design, can only produce fields that are described by Regular Solid Harmonics (RSH) $$$\mathcal{R}_{n}^{m}$$$. However, depending on the location of the sources of inhomogeneity relative to the anatomy being shimmed, both RSH and Irregular Solid Harmonics (ISH) $$$\mathcal{I}_{n}^{m}$$$ will describe the inhomogeneous field. ISH field components cannot be zeroed-out by RSH fields produced by the external shimming system, limiting the shimming capabilities of any system.

By localizing field sources that cause inhomogeneity in the brain field, we verify the impossibility of a perfect magnetic field homogenization by external shim hardware. Then, the best homogeneity achievable by any such system when performing global and slice-by-slice shimming is evaluated. Finally, we explore the benefits of performing localized shimming in 3D brain ROIs.

Methods

Using a 3D model of the human head, with magnetic susceptibilities of air and tissues set to $$$0,36.10^{-6}$$$ and $$$-9,03.10^{-6}$$$, respectively, the magnetic field source distribution around it is computed from the right side of the following equation^2(adapted):
$$\nabla^2(B_z(\textbf{x}))=\left(\nabla^2\chi(\textbf{x})-3\frac{\partial^2\chi(\textbf{x})}{\partial^2{z}}\right)\frac{B_0}{3}$$ where $$$\chi$$$ is the magnetic susceptibility of the medium. Voxels with non-zero Laplacian are considered magnetic sources.

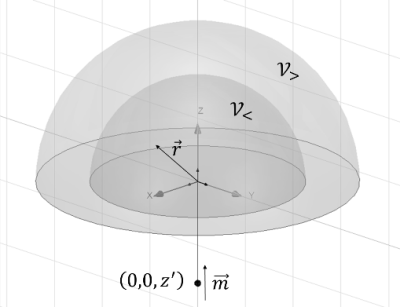
If field sources such as dipoles are located within the smallest sphere enclosing the shimming target, perfect homogenization using RSH is impossible. This can be illustrated by the configuration in Fig.1. The dipolar field source of inhomogeneity $$$\textbf{m}=m\hat{\textbf{z}}$$$, located at $$$(0,0,z')$$$, generates a magnetic field $$B_z(r,\theta)=\frac{\mu_0{m}}{2\pi}\left[r^2\frac{3\cos^2\theta-1}{2}-2rz'\cos\theta+z'^2\right]\frac{1}{\left(r^2-2rz'\cos\theta+z'^2\right)^{5/2}}$$ of Solid Harmonics expansion: $$B_z(r,\theta,\phi)=\frac{\mu_{0}m}{2\pi|z'|^3}\sum_{n=0}^{+\infty}\frac{(n+1)(n+2)}{2z'^n}\mathcal{R}_{n}^{0}(r,\theta,\phi)\;\text{for}\;\left|\frac{r}{z'}\right|<1\;(r\in\mathcal{V}_{<})$$ $$B_z(r,\theta,\phi)=\frac{\mu_{0}m}{2\pi{}z'^3}\sum_{n=2}^{+\infty}\frac{n(n-1)z'^{n+1}}{2}\mathcal{I}_{n}^{0}(r,\theta,\phi)\;\text{for}\;\left|\frac{r}{z'}\right|>1\;(r\in\mathcal{V}_{>}).$$ Thus, although $$$\nabla^2B_z=0$$$ in $$$\mathcal{V}_{<}\cup\mathcal{V}_{>}$$$, inhomogeneity can never be zeroed-out by RSH field patterns for $$$r>|z'|$$$, i.e. as long as the dipole is in the sphere encompassing the ROI.

A database of 100 three-dimensional $$$\Delta{}B_{0}$$$ brain maps was acquired after 2^nd-order shimming at a 3T Siemens Magnetom Prisma imager with 1.7-mm isotropic resolution, then scaled up by 7/3 for investigation at 7T. FSL’s brain extraction tool was used to ignore non-brain voxels. For each map in the database, both global and slice-by-slice RSH shimming are simulated from orders 3 to 14. Inhomogeneity is defined as the standard deviation of the $$$B_0$$$ field in the ROI while shimming performance is evaluated by the percentage reduction in inhomogeneity from the scanner 2^nd-order baseline.

Finally, for a single subject, a mask is created, consisting of three spheres, one of 6-cm diameter in the pre-frontal lobe, two of 5-cm in the temporal lobes, covering susceptibility-critical regions while avoiding intersection with sources. Then full 11th-order RSH shimming is simulated in this mask.

Results and Discussion

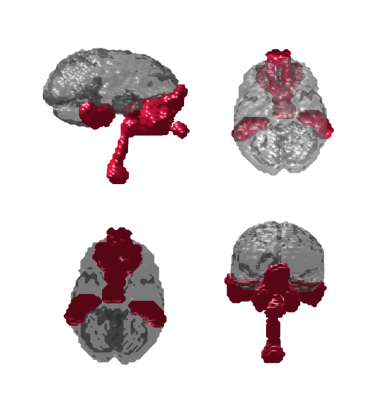
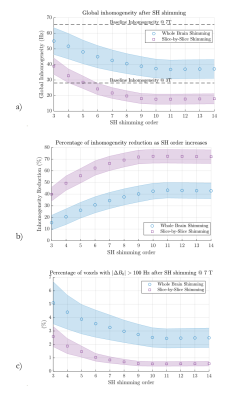
Figure 2 illustrates that magnetization-induced sources of inhomogeneity are disposed around the brain in such a way that it is impossible to obtain any brain-enclosing sphere that does not enclose sources. Therefore, RSH cannot zero-out the magnetic field excursion inside the brain even though $$$\Delta{}B_z^{\text{brain}}$$$

The impossibility of perfect shimming arising from the exposed configuration is reflected in the simulated shimming results in Figure 3. A plateau in inhomogeneity reduction is observed starting at order 11. It was checked that this result does not depend on image resolution by simulating shimming from downgraded $$$B_0$$$-maps with 3-mm voxels.

The plateau defines supremum inhomogeneity reduction, relative to baseline, of 43.4%(6.5) and 72.5%(5.8) for whole-brain and slice-by-slice shimming, respectively.

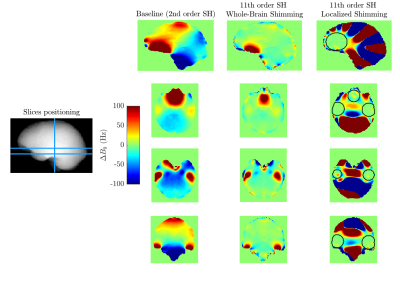
At maximum performance in whole-brain shimming, there are still wide regions with high-field excursion (over 100 Hz), notably close to the ear canals and around nasal conchae (cf. Figure 5).

While with slice-by-slice shimming, global inhomogeneity can ideally be brought to inferior levels than with whole-brain shimming, if high-resolution is envisioned, 2D-acquisitions can be a problem due to the lower signal emitted by each slice.

On the other hand, by targeting the most critical shimming regions with spherical ROIs, inhomogeneity decreases from 88.8 Hz to only 9.6 Hz, with a drop of the number of voxels over 100 Hz from 17.3% to a remarkable 0.1% (cf. Fig. 5). Inhomogeneity outside the target region is deeply compromised, but if only that shimming target is of interest for imaging, tailored inner volume selection could be performed to avoid aliasing artefacts.

Conclusion and perspectives

Due to intrinsic characteristics of the human head anatomy, static field inhomogeneity inside the human brain can never be fully mitigated by whole-brain shimming whatever the external hardware used. Nevertheless, by focusing shimming in brain ROIs, there is a potential for great improvement especially in regions close to the ear canals. Although the design of such focused shimming systems was not addressed here, we expect recent methodologies for optimal $$$B_0$$$ shimming Multi-Coil Array design^3,4 to be pertinent.

Acknowledgements

We would like to thank Guy Aubert and Nicolas Boulant for the insightful discussions leading to this work.