Introduction

Multi-Coil Arrays^1-3 (MCA) for $$$B_0$$$ shimming in the human brain have become a popular alternative to Spherical Harmonics (SH) shim coils in the past few years due to their relative easiness to build, better performance on whole-brain shimming and their ability to perform dynamic slice-by-slice⁴ shimming . These arrays are usually built so that circular coil windings are regularly distributed over a cylindrical surface, creating a matrix of channels, yet not strictly optimized for the human brain anatomy.

We proposed a new method^5,6 for designing optimized MCAs based on Singular Value Decomposition (SVD) of optimal Stream Functions⁷ (SF), providing loops of arbitrary geometry and optimally positioned to mitigate whole-brain inhomogeneity, showing, in simulations, superior performance to that of usual matrix MCAs (M-MCA) in whole-brain shimming while presenting a reduced channel count.

Nevertheless, assessment of slice-by-slice and region-specific shimming performances, of particular interest in high-resolution fMRI or spectroscopy, is also relevant to establish SF-SVD-based designs capable of satisfying several applications. Therefore, three brain Optimized MCA (O-MCA) designs are simulated in this work and compared to M-MCAs with increasing channel count.

Methods

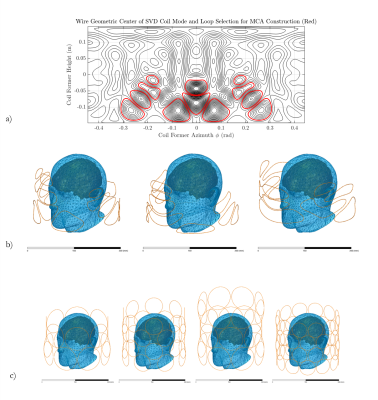
A 100-subject database of three-dimensional $$$\Delta{}B_0$$$ brain fieldmaps was built from 3T acquisitions in a Siemens Magnetom Prisma imager equipped with second-order SH shim coils at 1.7-mm isotropic resolution. The $$$\Delta{}B_0$$$ field intensities were rescaled to 7T, since a shim system for UHF is intended. FSL’s brain extraction tool was used to exclude non-brain voxels.

All fieldmaps are used as target fields, providing 100 SFs⁸ upon which SVD is applied⁹; then the optimized loops are extracted from the three first principal modes, each loop being associated with a shimming channel⁵. Three concentric cylindrical coil formers of equal length 300-mm and radii 140.5-mm, 149.5-mm and 158.5-mm accommodate the optimized loops extracted from first, second and third modes respectively, as shown in Fig. 1b. Single-turn models of each loop are exported to ANSYS®-Maxwell for the calculation of their magnetic field distribution (in a region enclosing all brains) and of their complex impedance. The loops are assumed to be 20-turn windings of copper wire with 1-mm diameter to improve shimming efficiency with limited power supply. Loop current is constrained to 5 A. Each winding is assumed to yield the same normalized magnetic field profile as a single turn.

For comparison purposes, four different M-MCAs of 16, 24, 32 and 48 circular loop channels over cylindrical formers of 140.5-mm radius are designed with similar windings and current constraints (cf. Fig.2a).

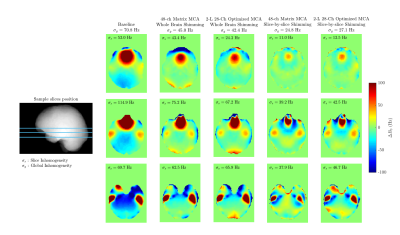
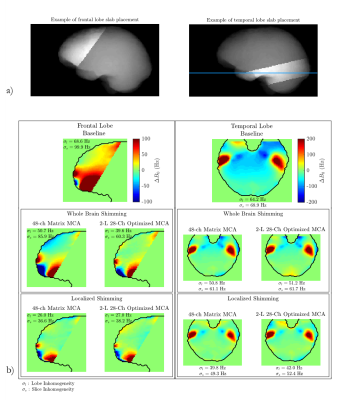
For every subject, the shimming performance of each MCA is simulated by computing the electric currents minimizing the $$$L_2$$$ norm of the residual magnetic field in the region of interest, which can be the whole-brain, a thin transverse slice or a slab covering some cerebral lobe depending on the application. Here the frontal and temporal lobes, known to be strongly affected by susceptibility gradients, are addressed with slabs located by hand on 20 randomly-chosen brains of our database. Finally, resulting inhomogeneity (=standard deviation of the residual across all voxels of interest), inhomogeneity reduction and power dissipation are assessed.

Results and Discussion

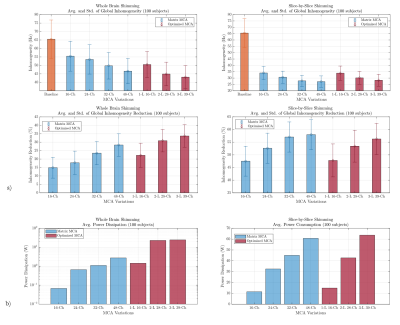
From Figures 2a and 4, O-MCAs outperform M-MCAs in whole-brain shimming while having much smaller channel count. The 2-layer, 28-channel O-MCA shows slightly better inhomogeneity reduction, 30.9%(6.7), on the database than the 48-channel M-MCA, 28.3%(6.7), and much superior performance than the 23.5%(6.9) achieved by 32-channel M-MCA, a relative improvement of 31.5%. From Figures 3a and 5, still in whole-brain shimming, O-MCAs show improvement in the frontal and temporal lobes compared to M-MCAs, not surprisingly in view of the channel concentration in front of these regions.

In slice-by-slice shimming, however, the regular distribution of channels in M-MCA is more advantageous, as the 32-channel MCA outperforms the 3-layer, 39-channel O-MCA. Nevertheless, inhomogeneity reduction achieved by 2-layer and 3-layer O-MCAs, at 53.4%(6.3) and 56.3%(6.2), respectively, are satisfactory compared to the 57.1%(5.9) and 58.0%(5.9) for 32-ch and 48-ch M-MCA.

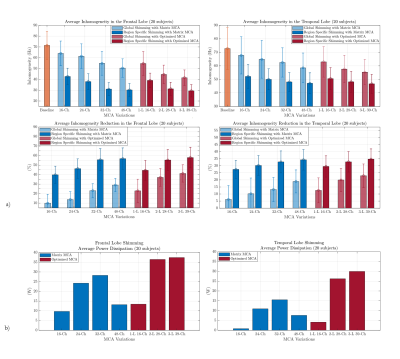
For region specific shimming, Figures 3a and 5, the 28-channel O-MCA inhomogeneity reduction for frontal and temporal lobes (55.4%(10.9) and 32.8%(7.3)) are very close to that achieved by 32-ch (55.6%(11.6) and 32.8%(7.8)) and 48-ch M-MCA (56.8%(11.2) and 34.3%(7.3)), while the 39-channel O-MCA outperforms them both by a small margin.

Within a design methodology, from Figure 2b, it is observed that power dissipation of the systems tends to increase with the homogeneity improvement, whether in slice-by-slice or whole-brain shimming. The 28-channel O-MCA produces 23.1W average dissipation for global shimming, much superior to the 2.8W dissipation of the 48-ch M-MCA. However, in slice-by-slice shimming, dissipation of the latter surpasses the 42.7W of the former by 18 W.

Conclusion and Perspectives

The SF-SVD-based optimization of MCAs is a powerful method for designing shimming systems with lower channel count, higher whole-brain shimming performance, while maintaining satisfactory results when used for slice-by-slice or focused shimming, in particular in the frontal lobe. The 2-layer, 28-channel system presents a good compromise between performance and channel count.

The present simulations resulted from an SF-SVD design targeting the whole brain. Further improvement of the optimized MCA performance could be attained if application-specific systems are envisioned, designed for addressing specific brain regions.

Acknowledgements

No acknowledgement found.