4195

Subject-specific local SAR assessment with corresponding estimated uncertainty based on Bayesian deep learning

E.F. Meliado^1,2,3, A. J. E. Raaijmakers^1,2,4, M. Maspero^2,5, M.H.F. Savenije^2,5, A. Sbrizzi^1,2, P.R. Luijten¹, and C.A.T. van den Berg^2,5
¹Department of Radiology, University Medical Center Utrecht, Utrecht, Netherlands, ²Computational Imaging Group for MR diagnostics & therapy, Center for Image Sciences, University Medical Center Utrecht, Utrecht, Netherlands, ³Tesla Dynamic Coils BV, Zaltbommel, Netherlands, ⁴Biomedical Image Analysis, Dept. Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands, ⁵Department of Radiotherapy, Division of Imaging & Oncology, University Medical Center Utrecht, Utrecht, Netherlands

Synopsis

For local SAR assessment, it is not possible to completely model the actual examination scenario, and residual experimental uncertainties are always present. Currently, no methods provide an estimate of the spatial distribution of confidence in the assessed local SAR. We present a Bayesian deep learning approach to map the relation between subject-specific complex B₁⁺-maps and the corresponding local SAR distribution, and to predict the spatial distribution of uncertainty at the same time. First results show the feasibility of the proposed approach providing potential for subject-specific reduction of uncertainties in peak local SAR assessment.

PURPOSE

Local specific absorption rate (SAR) cannot be measured directly and is usually evaluated by numerical electromagnetic simulations. Recently an alternative deep learning-based approach was presented¹. However, neither method provides any estimate of the confidence in the assessed local SAR.
It is not possible to completely model the actual examination scenario and therefore deviations between predicted and actual local SAR distributions are always present. Ideally, when a local SAR level is estimated, we would like to know the uncertainty of that estimation and the probability of underestimation. In another study, we propose a new correction approach based on conditional probability. However, that method is based on population-based error statistics of peak local SAR and does not provide a subject-specific spatial distribution of uncertainty.
In this study, we present a Bayesian deep learning approach to map the relation between subject-specific complex B₁⁺-maps and the corresponding local SAR distribution, and to predict the spatial distribution of estimation uncertainty at the same time. Initial results show the feasibility of this kind of approach providing new opportunities to improve the local SAR assessment.

THEORY

Bayesian neural networks allow capturing the model uncertainty². However, this kind of network usually comes with a prohibitive computational cost. A practical approach for variational Bayesian approximation is Monte Carlo (MC) dropout², which consists of temporarily removing a random number of nodes from the network during the training and at test time. Then, performing T stochastic forward passes through the network, the mean $$$\widehat{\mu}_i$$$ and variance $$$\widehat{\sigma}_{Model_i}^2$$$ of the approximate posterior Gaussian distribution can be calculated for each voxel i.

$$\widehat{\mu}_i=\frac{1}{T}\sum_{t=1}^T(output_i)_t$$ [1]

$$\widehat{\sigma}_{Model_i}^2=\frac{1}{T}\sum_{t=1}^T(output_i)_t^2-(\frac{1}{T}\sum_{t=1}^T(output_i)_t)^2$$ [2]

However, in Bayesian modeling, there are two main types of uncertainty³: (1) input data uncertainty, e.g. due to sensor noise, which cannot be reduced even if more training data were to be collected; (2) model uncertainty, e.g. due to out-of-training data, which can be reduced if enough training data are collected.
To capture data uncertainty a data-dependent noise parameter can be included in the loss function³. This allows the network to predict uncertainty by learning to mitigate the residual loss that depends on the data. Therefore, to model the data uncertainty a Gaussian likelihood estimation can be performed by adding the following minimization objective to the loss function.
$$\mathcal{L}_{Uncertanty}=\frac{1}{N_{voxel}}\sum_{i=1}^{N_{voxel}}\frac{1}{2}\frac{||ground\text{-}truth_i-output_i||^2}{\widehat{\sigma}_{Data_i}^2}+\frac{1}{2}\log\widehat{\sigma}_{Data_i}^2$$ [3]
Note that, "uncertainty labels" are not necessary, and $$$\widehat{\sigma}_{Data_i}^2$$$ is implicitly learned from the loss function. The second regularization term prevents the network from predicting infinite uncertainty for all data points.

METHODS

For the Bayesian approximation, we use a U-Net⁴ convolutional neural network with 50% MC dropout applied to every decoder layer (apart from the last). Similarly to our previous study¹, the convolutional neural network is trained to map the relation between the complex B₁⁺-map and the 10g-average SAR (SAR_10g) distribution. Using our database of 23 subject-specific models⁵ with an 8-fractionated dipole array^6,7 for prostate imaging at 7T, 23×250=5750 data samples are generated by driving the array with uniform input power (8×1W) and random phase settings. Then, the network is trained by minimizing the $$$\mathcal{L}_{Uncertanty}$$$ loss function.
To estimate the model uncertainty, for each complex B₁⁺-map fifty local SAR distributions are calculated with MC dropout (T=50). Mean $$$\widehat{\mu}_i$$$ and model variance $$$\widehat{\sigma}_{Model_i}^2$$$ are calculated as reported in the theory section.
Then, the overall predictive uncertainty $$$\widehat{\sigma}_i$$$ for each voxel i is evaluated.
$$\widehat{\sigma}_{Data_i}^2=\frac{1}{T}\sum_{t=1}^T(\widehat{\sigma}_{Data_i}^2)_t$$ [4]
$$\widehat{\sigma}_i=\sqrt{\widehat{\sigma}_{Model_i}^2+\widehat{\sigma}_{Data_i}^2}$$ [5]
To assess the feasibility of the proposed approach for local SAR uncertainty estimation, the dataset is partitioned into 3 sub-datasets according to the models that have generated the data samples and a 3-Fold Cross-Validation is performed.

RESULTS AND DISCUSSIONS

In Figure 1 some example results are reported of the 3-Fold Cross-Validation. It shows six predicted local SAR distributions ($$$\widehat{\mu}$$$) and the corresponding absolute error and overall estimated uncertainty ($$$\widehat{\sigma}$$$). The peak local SAR (pSAR_10g), the root-mean-square error (RMSE) of the absolute error, and the root-mean-square (RMS) of the estimated uncertainty are reported on top. They show a good qualitative and quantitative match between ground-truth and predicted SAR_10g distributions and between absolute error and estimated uncertainty.
Figure 2 shows for the same examples the estimated model uncertainty ($$$\widehat{\sigma}_{Model}$$$) and data uncertainty ($$$\widehat{\sigma}_{Data}$$$) distributions, highlighting a much greater contribution from the data uncertainty (about 5 times). This could indicate that we have provided sufficient training samples to learn the model. However, a higher probability of dropout (currently is 50%) might be required to increase the sensitivity to the model uncertainty.
To conclude in Figure 3 the scatter plots are reported of respectively predicted versus ground-truth peak local SAR and RMS estimated uncertainty versus RMSE absolute error, showing a good correlation in all cross-validations.
It is worth noting that we are more interested in estimating the uncertainty that leads to underestimation error. To this end, specific loss functions are under investigation.

CONCLUSION AND FUTURE WORK

The deep-learning based Bayesian approach allows feedback on the uncertainty of the local SAR estimate to be returned. Methods to take advantage of this now accessible information in terms of subject-specific safety factors will be part of future study.

Acknowledgements

No acknowledgement found.

References

Meliadò EF, Raaijmakers AJE, Sbrizzi A, et al. A deep learning method for image‐based subject‐specific local SAR assessment. Magn Reson Med. 2019;00:1–17.
Gal Y, Ghahramani Z. Dropout as a bayesian approximation: representing model uncertainty in deep learning. In: Proceedings of the 33rd International Conference on International Conference on Machine Learning, ICML. 2016;1050-1059.
Kendall A, Gal Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?. In: Advances in Neural Information Processing Systems. 2017;5580–5590.
O. Ronneberger, P. Fischer, T. Brox, U-Net: Convolutional Networks for Biomedical Image Segmentation, Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015 pp 234-241.
Meliadò EF, van den Berg CAT, Luijten PR, Raaijmakers AJE. Intersubject specific absorption rate variability analysis through construction of 23 realistic body models for prostate imaging at 7T. Magn Reson Med. 2019;81(3):2106-2119.
Steensma BR, Luttje M, Voogt IJ, et al. Comparing Signal-to-Noise Ratio for Prostate Imaging at 7T and 3T. J Magn Reson Imaging. 2019;49(5):1446-1455.
Raaijmakers AJE, Italiaander M, Voogt IJ, Luijten PR, Hoogduin JM, et al. The fractionated dipole antenna: A new antenna for body imaging at 7 Tesla. Magn Reson Med. 2016;75:1366–1374.

Figures

Figure 1: Six example results of the 3-Fold Cross-Validation: Ground-Truth local SAR distribution (first column), predicted local SAR distributions ($$$\widehat{\mu}$$$) – second column), absolute error (third column) and estimated uncertainty ($$$\widehat{\sigma}$$$) - fourth column). On top are reported the peak local SAR (pSAR_10g), the root-mean-square error (RMSE) of the absolute error, and the root-mean-square (RMS) of the estimated uncertainty.

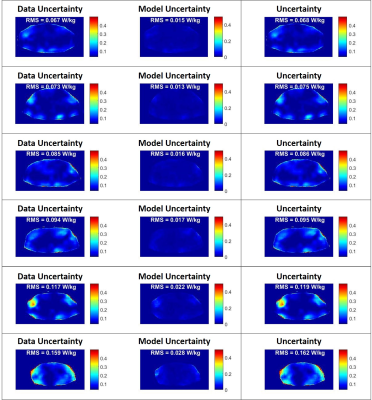
Figure 2: Six example results of the 3-Fold Cross-Validation: estimated data uncertainty distribution ($$$\widehat{\sigma}_{Data}$$$ - first column), model uncertainty distribution ($$$\widehat{\sigma}_{Model}$$$ - second column) and overall uncertainty distribution ($$$\widehat{\sigma}$$$ - third column). On top are reported the root-mean-square (RMS) of the estimated uncertainties.

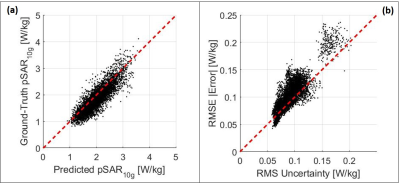
Figure 3: (a) Scatter plot predicted peak local SAR versus Ground-Truth peak local SAR. (b) Scatter plot RMS of the estimated uncertainty versus RMSE of the absolute error.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

4195