4181
A Temperature Prediction Workflow for DBS Electrodes Undergoing MRI1Department of Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2National Magnetic Resonance Research Center (UMRAM), Bilkent University, Ankara, Turkey, 3Center for Magnetic Resonance Research (CMRR), University of Minnesota, Minneapolis, MN, United States
Synopsis
We present a workflow consisting of a simple quasi-static EM model and a thermal transient simulation model for predicting temperature around commercial DBS electrodes. The model was able to predict the heating at a single contact accurately for different trajectories.
Intoduction
Radiofrequency (RF) heating of Deep Brain Stimulation (DBS) electrodes is an important patient safety problem in MRI1. The heating depends on various factors such as electrode geometry, trajectory, the RF coil geometry as well as the patient anatomy, therefore it is challenging to predict. In recent years, complex electrode models with realistic trajectories were studied using various EM simulation methods2-4. Although these studies are valuable for gaining insight for different factors that affect the heating (e.g., electrode trajectory, the effect of IPG), they are difficult to validate with experiments. Animal studies have been conducted in the past5 which provide useful information regarding the effect of tissue inhomogeneity and blood perfusion on the heating. However, since the lead trajectories vary from subject to subject they are not necessarily useful for predicting the outcome of RF heating in a patient. Therefore, patient-specific safety assessment is still an unmet medical need for patients with DBS electrodes.Transfer function-based models as well as transmission line/lumped element models have also been proposed in the past6-9. These models require less computational time in comparison to the full EM simulation approach. They are shown to be accurate for predicting heating in phantoms, however, their accuracy has not been demonstrated for non-homogeneous human tissue. In addition, the electric field’s component that is tangential to the electrode's trajectory is needed to calculate induced current on the electrode (and/or tip temperature), which is usually not known in advance.
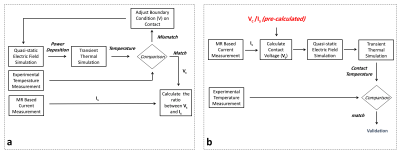
In this work, we propose a new workflow for predicting RF heating at the contact points of commercial DBS electrodes due to RF exposure in MRI (Fig. 1). We hypothesize that the current flowing on the shaft at a location near the tip is linearly proportional to the charge density on the contact (consequently the voltage on the contact). This proportionality is dependent on the electrode type as well as EM properties of the surrounding medium however it is independent of the trajectory of the electrode.
Theory and Method
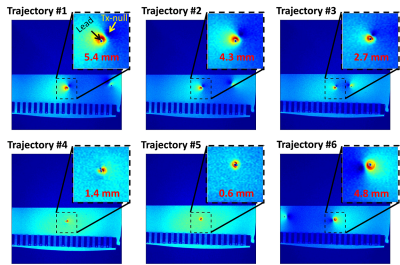
We used a simple quasi-static EM model (Sim4Life, Zurich) to solve the SAR distribution around the electrode contacts. The SAR distribution is then used as an input to the transient thermal simulation to generate temperature progression curves.In Part 1, we exposed a commercial electrode (directional lead for the Infinity DBS system, Abbott Laboratories, Chicago, IL) in a uniform phantom (trajectory #1) to RF energy in a 3T MR scanner, using a Turbo Spin Echo (TSE) MR sequence (FA=150o, TR=6000ms, Echo Train Length=15) and measured the temperature at a single contact. In addition, we measured the induced current Is on the shaft of the electrode at a pre-determined distance from the tip10 by measuring the distance between the DBS-lead and Tx-null in a 3D GRE image (TR/TE=20/2.64ms, in-plane resolution=0.5mm, slice thickness=3mm). Then we attempted to approximate the measured heating curve with our EM/thermal contact model. In the quasi-static EM model, the contact(s) are assigned a constant voltage (Vc) boundary condition (Fig. 2). The voltage is adjusted iteratively until the simulated and experimentally measured temperature curves matched. Once the match is achieved, the ratio between voltage Vc and the induced current on the shaft is calculated which is assumed to be constant regardless of the trajectory.
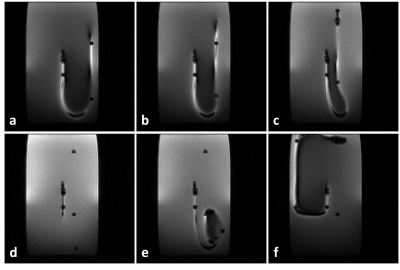
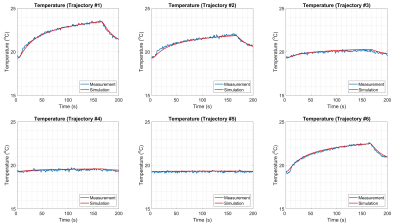
In part 2, we experimented with the same DBS electrode placed in the same phantom, in different trajectories as shown in Fig. 3. We exposed the electrode to RF energy via the same MR sequence as in part 1. We measured the temperature at the contact and measured Is for each trajectory. We also simulated the SAR around the contact by imposing a voltage boundary condition Vc (i.e., determined using the ratio in the previous part and measured Is) in the quasi-static EM simulation model. Finally, we calculated the contact temperature and compared the simulated and measured temperature curves for five different electrode trajectories.
Results
Fig. 4 shows the distances between the lead and Tx-nulls which are used for MR-based current measurement10.As shown in Fig. 5, we observed a quantitative match between simulated and measured temperature curves for all experiments (RMSE=0.12oC). The proposed method was able to predict the heating at a single contact accurately for five different trajectories.
Discussion
The current flowing at the shaft of the electrode (close to the tip) is linearly proportional to the charge density on the contact (as well as the voltage). This proportionality is experimentally shown to be independent of the trajectory of the electrode.Since this ratio is determined by the medium, its value should be equal in-vivo and in gel, as long as the EM properties of the gel is identical to human tissue. We did not validate this assumption in this work, however, we intend to investigate it in future studies.
IPG connection may also affect the RF heating of the electrode as previously shown9. The dependence/independence of the calculated ratio on IPG should also be investigated.
Conclusion
We present a workflow consisting of a simple quasi-static EM model and a thermal transient simulation model for predicting temperature around commercial DBS electrodes. The model was able to predict the heating at the contact of a commercial electrode accurately for different trajectories.Acknowledgements
This work was supported by following grant: NIBIB P41 EB027061References
1. Henderson JM, Tkach J, Phillips M, Baker K, Shellock FG, Rezai AR. Permanent neurological deficit related to magnetic resonance imaging in a patient with implanted deep brain stimulation electrodes for Parkinson's disease: case report. Neurosurgery 2005;57(5):E1063; discussion E63 doi: 10.1227/01.neu.0000180810.16964.3e[published Online First: Epub Date]|.
2. Guerin B, Iacono MI, Davids M, Dougherty D, Angelone LM, Wald LL. The 'virtual DBS population': five realistic computational models of deep brain stimulation patients for electromagnetic MR safety studies. Phys Med Biol 2019;64(3):035021 doi: 10.1088/1361-6560/aafce8[published Online First: Epub Date]|.
3. Guerin B, Serano P, Iacono MI, et al. Realistic modeling of deep brain stimulation implants for electromagnetic MRI safety studies. Phys Med Biol 2018;63(9):095015 doi: 10.1088/1361-6560/aabd50[published Online First: Epub Date]|.
4. Golestanirad L, Angelone LM, Iacono MI, Katnani H, Wald LL, Bonmassar G. Local SAR near deep brain stimulation (DBS) electrodes at 64 and 127 MHz: A simulation study of the effect of extracranial loops. Magn Reson Med 2017;78(4):1558-65 doi: 10.1002/mrm.26535[published Online First: Epub Date]|.
5. Shrivastava D, Abosch A, Hughes J, et al. Heating induced near deep brain stimulation lead electrodes during magnetic resonance imaging with a 3 T transceive volume head coil. Phys Med Biol 2012;57(17):5651-65 doi: 10.1088/0031-9155/57/17/5651[published Online First: Epub Date]|.
6. Tokaya JP, Raaijmakers AJE, Luijten PR, Bakker JF, van den Berg CAT. MRI-based transfer function determination for the assessment of implant safety. Magn Reson Med 2017;78(6):2449-59 doi: 10.1002/mrm.26613[published Online First: Epub Date]|.
7. Tokaya JP, Raaijmakers AJE, Luijten PR, van den Berg CAT. MRI-based, wireless determination of the transfer function of a linear implant: Introduction of the transfer matrix. Magn Reson Med 2018;80(6):2771-84 doi: 10.1002/mrm.27218[published Online First: Epub Date]|.
8. Acikel V, Atalar E. Modeling of radio-frequency induced currents on lead wires during MR imaging using a modified transmission line method. Med Phys 2011;38(12):6623-32 doi: 10.1118/1.3662865[published Online First: Epub Date]|.
9. Acikel V, Uslubas A, Atalar E. Modeling of electrodes and implantable pulse generator cases for the analysis of implant tip heating under MR imaging. Med Phys 2015;42(7):3922-31 doi: 10.1118/1.4921019[published Online First: Epub Date]|.
10. Eryaman Y, Kobayashi N, Moen S, et al. A simple geometric analysis method for measuring and mitigating RF induced currents on Deep Brain Stimulation leads by multichannel transmission/reception. Neuroimage 2019;184:658-68 doi: 10.1016/j.neuroimage.2018.09.072[published Online First: Epub Date]|.
Figures