Introduction

To date, the most widely used technique for monitoring thermal therapies is magnetic resonance thermometry via the proton resonance frequency shift (PRFS) method. In this method, temperature rise computation involves subtracting a reference phase map from the current phase map, which makes it prone to errors stemming from tissue motion and external perturbations of the magnetic field. Salomir et al.¹ and Kickhefel et al. ² proposed a reference-free PRFS thermometry technique for 2-D acquisitions, based on near-harmonic 2-D reconstruction of the background phase from the measured phase values on a thin, nearly-closed unheated border around the heated region. This study extends the reference-free PRFS thermometry method^1,2 to 3-D data, by performing near-harmonic reconstruction of the background phase inside a sphere.

Method

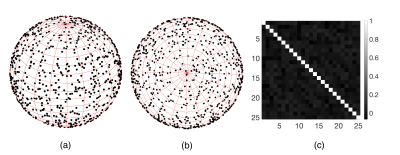
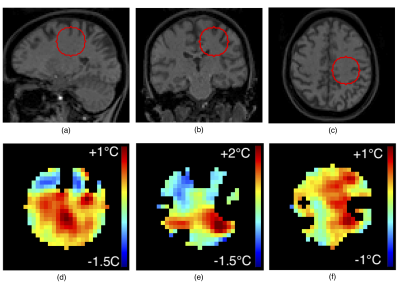
Experimental data was acquired with a 3-D FLASH sequence (TE/TR=5/8ms,BW=600HZ/pixel,FA=12°, water-selective binomial, voxel size=2mm isotropic) on a 3T whole-body MRI scanner for two scenarios: ex-vivo high intensity focused ultrasound (HIFU) sonication of a tissue-mimicking gel using a single-loop coil (PF=6/8x6/8, acquisition time=25s), and in-vivo acquisitions of a human voluntary brain (“zero-measurement”) using a 64-channel coil and CAIPIRINHA=3x2 (PF=7/8x7/8, acquisition time=10s). HIFU was generated by an MR-compatible phased array transducer (256 elements, operating at 1MHz). Reference-free reconstruction of the background phase was performed inside the volume of a sphere whose discretized surface (1 voxel thick) was assumed to be unheated. The background phase map was modeled as a harmonic function (i.e. whose Laplacian is null) plus a second order polynomial (non-harmonic component) in regions with homogenous or linearly varying magnetic susceptibility¹. We aimed to solve the inner Dirichlet problem. After removing the non-harmonic component (i.e. constant Laplacian) using the differential of the mean value on two concentric spheres, the harmonic component of the background phase on the surface of a sphere of radius $$$R_0$$$ and polar coordinates $$$\theta\in[0,\pi),\varphi\in[0,2\pi)$$$ was approximated as a linear combination of real spherical harmonic functions $$$C_l^m(\theta,\varphi),S_l^m(\theta,\varphi)$$$ with coefficients $$$a_{lm},b_{lm}$$$: $$\Phi_{bk}(r=R_0,\theta,\varphi)\approx\sum_{l=0}^L\sum_{m=0}^l\left[a_{lm}C_l^m(\theta,\varphi)+ b_{lm}S_l^m(\theta,\varphi)\right], \quad (1)$$ where $$C_l^m(\theta,\varphi)=N_{lm}\cdot P_l^m(\cos \theta)\cdot\cos(m\varphi)$$ $$S_l^m(\theta,\varphi)=N_{lm}\cdot P_l^m(\cos\theta)\cdot\sin(m \varphi)$$ $$$P_l^m$$$ – Legendre polynomials and $$$N_l^m=\sqrt{\frac{2l+1}{4\pi}\cdot\frac{(l-m)\,!}{(l+m)\,!}}.$$$ The background phase of each voxel inside the sphere volume ($$$r<R_0$$$) was then estimated as: $$\Phi_{bk}(r,\theta,\varphi)\approx\sum_{l=0}^L\left(\frac{r}{R_0}\right)^l\sum_{m=0}^l\left[a_{lm}C_l^m(\theta,\varphi)+b_{lm}S_l^m(\theta,\varphi)\right]. \quad (2)$$ To solve for $$$a_{lm},b_{lm}$$$ from eq. (1), a uniform sample distribution on the sphere surface (Fig.1a,b) was obtained by Monte Carlo random sampling of $$$\varphi$$$ from a uniform distribution on $$$[0,2\pi)$$$, and of $$$\cos\theta$$$ from a uniform distribution on $$$[-1,1)$$$. This is because the differential area element on a unit sphere is: $$$d\Omega=\sin\theta d\theta d\varphi = -d(\cos\theta)d\varphi$$$. The orthonormality of the sampled spherical harmonic functions can be verified by inspecting the matrix of their pairwise dot products (Fig.1c). The number of samples was empirically chosen as proportional to the sphere surface: $$$N=\lfloor 4\pi(R_0)^2\rfloor$$$. Sample uncertainty was considered by weighing with corresponding magnitude data (low magnitude = high uncertainty). Equation (1) was written as $$$W\cdot\Phi_{bk}=W\cdot CS\cdot v,$$$ with $$$W$$$ – the $$$N\times N$$$ diagonal matrix of weights given by sample magnitude values, $$$\Phi_{bk}$$$ – the $$$N\times 1$$$ vector of phase data, $$$CS$$$ – the $$$N\times (L+1)^2$$$ matrix of sampled spherical functions, and $$$v$$$ – the $$$(L+1)^2\times 1$$$ vector concatenating coefficients $$$a_{lm},b_{lm}$$$. Vector $$$v$$$ was extracted as $$$v=(CS ^\top\cdot W\cdot CS)^{-1}\cdot(CS^\top\cdot W\cdot\Phi_{bk})$$$, allowing background phase estimation inside the sphere with eq.(2). For comparison, time-referenced PRFS temperature elevation maps were computed by subtraction of a reference phase map, and background phase drift correction using an unheated volume. For both scenarios we used $$$L=4$$$ and sphere radius = 10 voxels. For the in-vivo scenario, cerebro-spinal fluid (CSF) was excluded from data sampling due to susceptibility contrast. In a real treatment scenario, CSF would not be targeted by HIFU.

Results

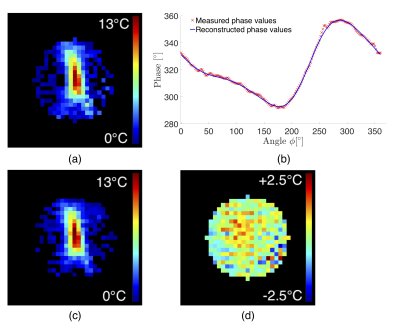
For the ex-vivo sonication, endpoint temperature elevation maps obtained with the proposed reference-free method and with the time-referenced PRFS method are in close agreement (Fig.2a,b). “Zero-measurement” comparison (Fig.2d) revealed good method precision (0.78°C) and accuracy (0.28°C). Measured and reconstructed phase values along an equatorial circle on the sphere closely match (difference standard deviation = 0.96°). “Zero-measurement” reference-free temperature maps from in-vivo acquisitions (Fig.3) confirmed good method accuracy (0.57°C) and precision (0.29°C). Average computation time was 75ms per temperature map (radius = 10 voxels) on a 3.4GHz processor. No ill-conditioned operation occurred.

Discussion

The good precision and accuracy of the proposed method, its fast computation times, and its results’ similarity with the time-referenced PRFS method for motion-free sonication, support its application to real-time temperature monitoring in tissues with homogenous or linearly varying magnetic susceptibility. Its main advantage compared to the time-referenced PRFS method is its robustness against inter-scan motion. The 3-D geometry is a natural mathematical framework for near-harmonic functions, contrary to the previous 2-D approach, involving analytical approximation on a restricted subspace^1,2. The main limitation of the method is the need for a user-provided unheated border, and its adaptation to potential tissue motion, which could be tackled by tissue tracking. The approach can be coupled with a fast acquisition (TWIST-VIBE, compressed sensing) to improve temporal resolution and address abdominal targets.

Conclusion

The proposed reference-free PRFS thermometry method constitutes a promising alternative to the time-referenced PRFS method, especially valuable during sonication of moving tissues.

Acknowledgements

No acknowledgement found.