4129
On-the-fly 3D images generation from a single k-space readout using a pre-learned spatial subspace: Towards MR-guided therapy and intervention1Department of Bioengineering, UCLA, Los Angeles, CA, United States, 2Biomedical Imaging Research Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, 3Siemens Healthineers, Los Angeles, CA, United States, 4Department of Medicine, UCLA, Los Angeles, CA, United States
Synopsis
A new real-time imaging scheme is proposed based on low-rank spatiotemporal decomposition. Briefly, a high-quality spatial subspace and a direct linear mapping from k-space navigator data to subspace coordinates are first learned from a “demo” scan. In the subsequent “live” scan, successive real-time images can be generated by a fast matrix multiplication procedure on a single instance of the k-space navigator readout (e.g. a single k-space line), which can be acquired at a high temporal rate. The method was demonstrated in vivo using a T1-T2 abdominal multitasking sequence.
Introduction
Real-time MR imaging with on-the-fly image generation is important for MR guided therapies and interventions1,2. However, it is still technically challenging to acquire real-time images with both high image quality and high temporal resolution. In this work, we propose a new real-time imaging scheme based on low-rank spatiotemporal decomposition (Fig. 1). Briefly, a high-quality spatial subspace and a direct linear mapping from k-space navigator data to subspace coordinates are first learned from a “demo” scan. In the subsequent “live” scan, successive real-time images can be generated by a fast matrix multiplication procedure on a single instance of the k-space navigator readout (e.g. a single k-space line), which can be acquired at a high temporal rate. Here we demonstrate this method in vivo using a T1-T2 abdominal multitasking sequence3.Theory
As in [4], the 4D image $$$I(x,t)$$$ can be modeled as a low-rank matrix $$$\bf A$$$ (Eq. 1)$$\bf A=U_x\Phi$$
where $$$\bf U_x$$$$$$\in C^{J \times L}$$$ contains $$$L$$$ spatial basis functions with $$$J$$$ total voxels, and $$$\bf \Phi$$$ $$$\in C^{L \times N_t}$$$ contains temporal weighting functions (depicting relaxation, motion, contrast changes, etc.). The real-time image at each time point $$$t$$$ can then be expressed as a linear combination of the spatial basis functions, weighted by $$$\bf \Phi$$$$$$_{:,t}$$$ (the column of $$$\bf \Phi$$$ corresponding to time point $$$t$$$), as illustrated in Fig. 2.
$$$\bf \Phi$$$ can be constructed as a linear combination of k-space navigator data $$$\bf D_{tr}$$$$$$\in C^{M \times N_t}$$$, which represents a very small subset ($$$M<J$$$) of k-space locations (a single central k-space line is often used) sampled more frequently than the rest of k-space throughout the scan5-7. Because $$$\bf \Phi$$$ is often extracted from the right singular vectors of $$$\bf D_{tr}$$$, there exists a linear transformation given by $$$\bf T$$$$$$\in C^{L \times M}$$$ that maps $$$\bf D_{tr}$$$ to $$$\bf \Phi$$$ as $$$\bf \Phi = T D_{tr}$$$. It follows that for an individual time point $$$t$$$, a single navigator line $$$\bf D$$$$$$_{:,t} \in C^{M \times 1}$$$ can be transformed into $$$\bf \Phi$$$$$$_{:,t}$$$ using (Eq. 2):
$$\bf \Phi_{:,t} = T D_{:,t}$$
Because the $$$\bf \Phi$$$$$$_{:,t}$$$ are the temporal weights of $$$\bf U_x$$$, the entire 3D image at $$$t$$$ can be generated from $$$\bf D$$$$$$_{:,t}$$$ according to simple matrix multiplication (Eq. 3):
$$\bf A_{:,t} = U_x T D_{:,t}$$
Note that both $$$\bf T$$$ and $$$\bf U_x$$$ should remain unchanged with further acquisition in the same imaging session unless abrupt body motion or novel contrast mechanisms force the new images outside of the range of (the spatial subspace). Therefore, if we can learn $$$\bf U_x$$$ and $$$\bf T$$$ from an initial “demo” scan, then we can acquire only navigator data afterwards in a “live” phase (Fig. 1), applying Eq. 3 to quickly and easily generate real-time 3D images.
Methods
The proposed method was tested using a sequence originally used for abdominal T1/T2 multitasking3, as shown in Fig. 3. Specific imaging parameters were: matrix size=160x160x52, FOV=275x275x240mm3, voxel size=1.7x1.7x6mm3, TR/TE=6.0/2.1ms, flip angle=5° (following SR preparation) and 10° (following T2 preparation), water-excitation for fat suppression. Total imaging time was approximately 8 minutes.Experiments were performed in two healthy subjects (n=2) on a 3.0 T clinical scanner (MAGNETOM Skyra; Siemens Healthineers) equipped with an 18-channel phase array body coil. Two identical Multitasking scans were performed successively, with the first one used as the “demo” scan to learn the spatial basis $$$\bf U_x$$$ and linear transformation matrix $$$\bf T$$$, and the second scan used as the “live” scan. At an arbitrarily chosen time point in the “live” scan, the real-time 3D image set was reconstructed using the data of the entire scan based on the regular Multitasking algorithm5 (as a reference) or using the navigator line only based on the proposed method. Image quality and delineation of motion state were evaluated at different time points corresponding T1w, T2w and PDw respectively.
Results
The average elapsed time to transform a navigator readout and weight the spatial basis in the live phase was ~40 ms per entire 3D volume. Since the navigator data (central k-space line) was acquired in 6 ms, a temporal resolution of 50 ms or less can be reached.Fig. 4 shows the comparison between the results of Multitasking reconstruction (reference) and the proposed real-time reconstruction. The motion state and contrast in the real-time reconstruction were in excellent agreement with the reference. Fig. 5 is a real-time display of 3D images reconstructed with the proposed method.
Discussion and Conclusion
With a pre-learned high-quality spatial subspace, real-time images with both high spatial and temporal resolution can be generated.The very high-speed reconstruction (40 ms per 3D volume) builds on a fast matrix multiplication procedure. Because the real-time reconstruction operator is capable of reconstructing any image along a continuum within the known spatial subspace, it does not rely on binning to select an image from a discrete dictionary of potential results8 and supports multi-contrast imaging. This scheme can potentially be extended to work in a low-rank tensor (LRT) framework such as MR Multitasking, which may in turn provide an avenue to produce contrast-transformed T1 or T2-only real-time imaging even without further sequence changes.
Acknowledgements
No acknowledgement found.References
- Rieke V, Butts Pauly K. MR thermometry. Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2008 Feb;27(2):376-90.
- Lagendijk JJ, Raaymakers BW, Van den Berg CA, Moerland MA, Philippens ME, Van Vulpen M. MR guidance in radiotherapy. Physics in Medicine & Biology. 2014 Oct 16;59(21):R349.
- Deng Z, Christodoulou AG, Wang N, Yang W, Wang L, Lao Y, Han F, Bi X, Sun B, Pandol S, Tuli R, Li D, Fan Z. Free-breathing Volumetric Body Imaging for Combined Qualitative and Quantitative Tissue Assessment using MR Multitasking. In Proceedings of the 27th Annual Meeting of ISMRM 2019 (p. 0698).
- Liang ZP. Spatiotemporal imaging with partially separable functions. In 2007 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro 2007 Apr 12 (pp. 988-991). IEEE.
- Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, Li D. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nature biomedical engineering. 2018 Apr;2(4):215.
- Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magnetic resonance in medicine. 2016 Feb;75(2):775-88.
- Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR. IEEE transactions on medical imaging. 2011 Jan 31;30(5):1042-54.
- Feng L, Otazo R. Magnetic Resonance SIGnature MAtching (MRSIGMA) for Real-Time Volumetric Motion Tracking. In Proceedings of the 27th Annual Meeting of ISMRM 2019 (p. 0578).
Figures
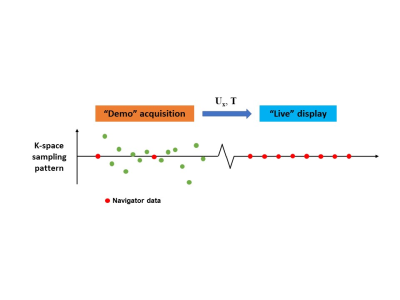
Figure 1: The proposed real-time imaging scheme.
A high-quality spatial subspace and a direct linear mapping from k-space navigator data to subspace coordinates are first learned from a “demo” scan. In the subsequent “live” scan, successive real-time images can be generated by a fast matrix multiplication procedure on a single instance of the k-space navigator readout (e.g. a single k-space line), which can be acquired at a high temporal rate.
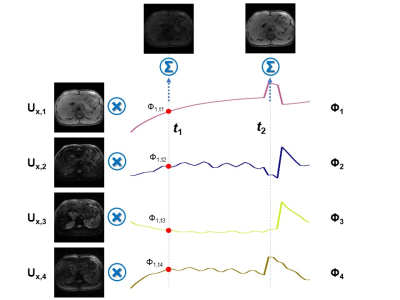
Figure 2: Illustration of the low-rank spatiotemporal decomposition.
The real-time image at specific time point t can be expressed as a linear combination of the spatial basis functions, weighted by the values of the temporal weighting at time point t.
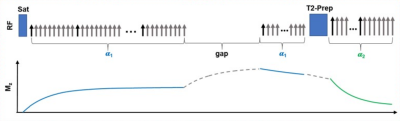
Figure 3: Sequence design for the experiment.
The k-space is continuously sampled using a stack-of-stars GRE sequence with golden angle ordering in the x-y plane and Gaussian-density randomized ordering in the z direction, interleaved with navigator data (0° in-plane, central partition) every 10th readout. A saturation recovery (SR) preparation and T2 preparation are combined to generate T1-weighted and T2-weighted signals during magnetization evolution.
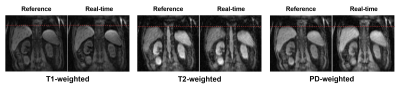
Figure 4: Results from Multitasking reconstruction (reference) and the proposed real-time reconstruction (Subject 1).
The motion state and contrast in the real-time reconstruction were in excellent agreement with the reference.

Figure 5: Real-time movies reconstructed from the proposed method (Subject 2).
The video was generated using the real-time reconstruction results with a frame rate consistent with the real scan. Both motion and contrast change can be clearly seen in the movie.