Introduction

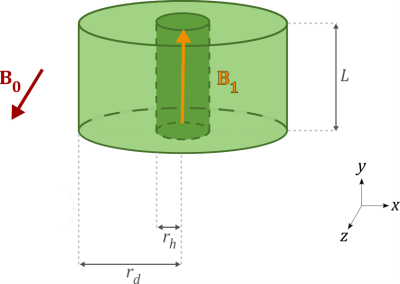
Magnetic Resonance Microscopy (MRM) aims at imaging small samples with very high spatial resolution (<< 100 μm) using B₀ field strengths between 7 T and 22 T¹. At such fields, the conventional RF coil is the solenoid. However, for lossy biological samples, its ultimate Signal-to-Noise Ratio (SNR) is intrinsically limited by the significant electric field within the sample². Dielectric resonators are an alternative probe design to tackle this issue^3,4: high-permittivity rings support eigenmodes whose frequency characteristics rely on the resonator dimensions and the material properties^5,6. The first transverse electric mode (TE_01δ) produces a strong B₁ excitation field (Fig. 1), and a low E-field. Here we present a semi-analytical model (SAM) to design dielectric ring probes with high SNR⁷. This model is validated with numerical simulations and experimentally tested for MRM at 17.2 T⁸.

Methods

The noise is dominated by losses in the dielectric ring (volume $$$V_\mathbf{ring}$$$, outer and inner radii $$$r_\mathbf{d}$$$ and $$$r_\mathbf{h}$$$, height $$$L$$$, permittivity $$$\epsilon_\mathbf{r}$$$) and in the sample (volume $$$V_\mathbf{samp}$$$, radius $$$r_\mathbf{h}$$$, height $$$L$$$, electrical conductivity $$$\sigma_\mathbf{samp}$$$). The SNR is proportional to the SNR factor (Eq. 1) with $$$H_\mathbf{samp}(0)$$$ the H-field amplitude in the sample, and (Eq. 2)⁹ the total dielectric losses.
(Eq. 1) $$u_\mathbf{SNR}=H_\mathbf{samp}(0)/\sqrt{P_\mathbf{loss}}$$
(Eq. 2) $$P_\mathbf{loss}=\frac{1}{2}\omega\epsilon''\int_{V_\mathbf{ring}}|\mathrm{E}|^2dv+\frac{1}{2}\sigma_\mathbf{samp}\int_{V_\mathbf{samp}}|\mathrm{E}|^2dv$$
The TE_01δ mode field is described by Bessel and Hankel functions in cylindrical coordinates $$$\left(\rho,\theta,y\right)$$$. As this mode has a cylindrical symmetry, $$$H_y$$$, $$$H_\rho$$$ and $$$E_\theta$$$ are the only nonzero components¹⁰. Expressing $$$H_y$$$, as in Eqs. 3-4 with $$$\alpha_\Omega$$$ and $$$\beta_\Omega$$$ the wavenumbers in region $$$\Omega$$$, enables to derive the other components^11,12.
(Eq. 3)$$H_\mathbf{y,samp}\left(\rho,y\right)\propto J_\mathbf{0}\left(\alpha_\mathbf{samp}\rho\right)\cos\left(\beta_\mathbf{samp}y\right)$$
(Eq. 4)$$H_\mathbf{y,ring}\left(\rho,y\right)\propto \left[H_\mathbf{0}^\mathbf{(1)}\left(\alpha_\mathbf{ring}\rho\right)+\xi H_\mathbf{0}^\mathbf{(2)}\left(\alpha_\mathbf{ring}\rho\right)\right]\cos\left(\beta_\mathbf{ring}y\right)$$
The E-field, derived from the spatial derivative of $$$H_\mathbf{y}$$$, is proportional to the H-field amplitude. In Eq. 3, this amplitude is $$$H_\mathbf{samp}(0)$$$. To analytically express dielectric losses, the probe EM field is simplified to that of the corresponding disk: $$$\mathrm{E}\left(\overrightarrow{r}\right)_{|ring}=\mathrm{E}\left(\overrightarrow{r}\right)_{|disk}$$$, $$$\mathrm{E}\left(\overrightarrow{r}\right)_{|samp}=\tau\mathrm{E}\left(\overrightarrow{r}\right)_{|disk}$$$ and $$$\mathrm{E}\left(\overrightarrow{r}\right)_{|disk}\propto J_\mathbf{1}\left(\alpha_\mathbf{disk}\rho\right)$$$. $$$\tau$$$ reflects the amplitude decrease from permittivity contrast between the sample and the ring. Eq. 1 becomes Eq. 5 with $$$P_\mathbf{loss,norm}^\mathbf{i}=P_\mathbf{loss}^\mathbf{i}/|H_\mathbf{disk}(0)|^2$$$.
(Eq. 5) $$u_\mathbf{SNR}^\mathbf{DR}=\tau/\sqrt{P_\mathbf{loss,norm}^\mathbf{ring}+\tau^2 P_\mathbf{loss,norm}^\mathbf{samp}}$$
A Frequency Domain Solver (CST Microwave Studio) was used to evaluate the field distribution of the mode excited in the dielectric probe by a 1 cm diameter non-resonant loop. In a “combined method”, the SNR factor is computed with Eq. 5 applied to the field exported from numerical simulations run in the CST Eigenmode Solver (mesh step: 0.2 mm isotropic).
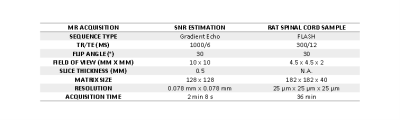
The experimental resonator was built with a ferroelectric ceramic⁸ with the following parameters at 730 MHz (Larmor frequency at 17.2 T): $$$r_\mathbf{d}$$$ = 9 mm, $$$r_\mathbf{h}$$$ = 2.8 mm, $$$L$$$ = 10 mm, $$$\epsilon_\mathbf{r}$$$ = 536, $$$\tan\delta$$$ = $$$8\times 10^{-4}$$$. The phantom used was a tube of diameter 4.5 mm and length 12 mm filled with a solution of permittivity $$$\epsilon_\mathbf{r,test}$$$ = 50 and conductivity $$$\sigma_\mathbf{test}$$$ = 1 S/m. The corresponding optimal solenoid has 4 turns, 7 mm diameter, 12 mm length and is made with 1.5 diameter copper wire². Its SNR factor can be found in the literature². MRI acquisitions were performed on a preclinical device (Bruker BioSpin, Ettlingen, Germany) equipped with a triaxial gradient system of maximum strength 1 T/m. The biological sample studied was a chemically fixed rat spinal cord. MR acquisitions were performed with sequences described in Fig. 2.

Results

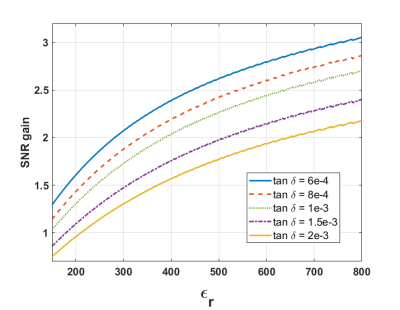
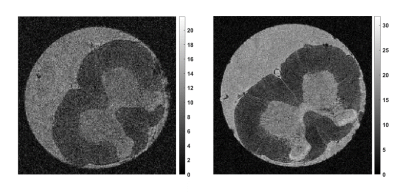
The SAM was used to estimate the SNR gain $$$u_\mathbf{SNR}^\mathbf{DR}/u_\mathbf{SNR}^\mathbf{sol}$$$, plotted in Fig. 3 for the phantom as a function of the dielectric properties. For each permittivity, $$$r_\mathbf{d}$$$ was adapted to adjust the TE_01δ mode to the Larmor frequency. When $$$\tan\delta \leq 2 \times 10^{-3}$$$ and $$$\epsilon_\mathbf{r}\geq 220$$$, the semi-analytical method predicts a higher SNR with the dielectric probe than with the optimal solenoid. From this dependency, the prototype properties were selected, resulting in a theoretical SNR gain of 2.5. The prototype SNR factor was computed using the SAM and compared to numerical simulations and a combined method as shown in Fig. 4. The sample permittivities were 50 and 81 and its conductivity was varied from 0 to 2.5 S/m. The relative error between the SAM and the commercial software was always below 8%⁷. Finally, experiments performed on the test solution resulted in a measured SNR gain of 2.2 (versus 2.5 theoretically), as obtained with numerical simulations. Fig. 5 demonstrates that the ceramic probe performs better than the optimal solenoid when imaging the biological sample, with an SNR gain of 1.45.

Discussion

The SAM estimates the SNR factor with an error lower than 8% over a large range of electromagnetic properties. The SNR gain estimation was validated in one case, in which the predicted value was within 15% of the experimentally measured value.

Conclusion

This study focused on the modelling of dielectric ring probes in which the first TE mode is excited to generate the B1 field used in MR acquisitions. The semi-analytical model predicts the performance of such probes with a good accuracy and can be used as a design guideline. Our current and future work includes the extension of dielectric probes modelling to clinical applications. This includes resonators with human scale dimensions, as well as the study of higher resonant modes (like HEM modes).

Acknowledgements

This project received funding from the European Union’s Horizon 2020 Research and Innovation programme (grant No 736937) and from an ERC Advanced Grant (NOMA-MRI 670629). S.G. acknowledges the support by the President of the Russian Federation (МК-3620.2019.8).