Purpose

For regular MR arrays comprised of circles, hexagons and squares the critical overlap for minimized magnetic coupling was well documented e.g. [1], however an array of isotropic uniform ellipses was not mentioned. We are trying to give coil designers a simple chart for laying out an elliptical array.

Theory

First, let us define an ellipse parametrically. Let $$$a$$$ and $$$b$$$ represent the two radii of the ellipse. Then the ellipse description is given by $$$\mathbf{r}(t)\equiv \{a\cos t,b\sin t\}$$$ where $$$t\in \left[0,2\pi \right]$$$. We will call the elliptical array uniform if all ellipses have the same $$$a$$$ and $$$b$$$. The array is isotropic if the major axes of the ellipses are colinear. Critical overlap is found minimizing the mutual inductance between ellipses. We will utilize the expression for mutual inductance evaluation from [2].
We can find the mutual inductance between two congruent and isotropic ellipses as a function of separation parameters $$$Δx=|x_i-x_j|$$$ and $$$Δy=|y_i-y_j|$$$. Let us define the overlap coefficients in horizontal direction as $$$k_a=2 a/Δx$$$ and in vertical direction as $$$k_b=2 b/Δy$$$, where the $$$a$$$, $$$b$$$ and $$$x_i$$$, $$$y_i$$$ corresponds respectively to horizontal and vertical radii of the ellipse and their coordinates.
For a given size ellipses with fixed $$$a$$$ and $$$ε=b/a$$$, the mutual inductance takes the form
$$M(k_a,k_b)=\frac{\mu_0}{ 4 \pi}a\int_{0}^{2\pi}\int_{0}^{2\pi}\frac{\sin t_1 \sin t_2+ε^2 \cos t_1\cos t_2}{\sqrt{(2/k_a+(\cos t_1-\cos t_2))^2+ε^2 (2/k_b+(\sin t_1-\sin t_2))^2}}d t_1 d t_2$$(1)
From equation (1) , the critically overlapped ellipses ($$$M_{crit}\equiv 0$$$) are found for specific adimensional parameters $$$ε$$$, $$$k_a$$$ and $$$k_b$$$ by minimizing the functional (1). This result shows that critically overlapped ellipses are scalable (within quasistatic approximation).
Let us introduce the following definitions: the distance between two ellipses’ centers
$$Δs=\sqrt{Δx^2+Δy^2}=\frac{2 a}{k_a}\sqrt{1+\left (\frac{ε k_a}{k_b}\right )^2}$$(2)
and oblique diameter
$$d=2\sqrt{a^2 \cos ^2 α+b^2 \sin ^2 α}=2 a \cos α \sqrt{1+ε^2 \tan ^2 α}$$(3)
Considering that the angle between ellipses is $$$\tan α=Δy/Δx=ε k_a / k_b$$$ the oblique overlap can be defined as $$k=\frac{d}{Δs}=k_a \frac{\sqrt{1+ε^2 \tan ^2 α}}{1+ε^2 \tan ^2 α}$$(4)
In equation (1) the cartesian overlapping coefficients $$$k_a$$$ and $$$k_b$$$ can be substituted with functions of oblique overlapping coefficient $$$k$$$ and angle $$$α$$$.

Results

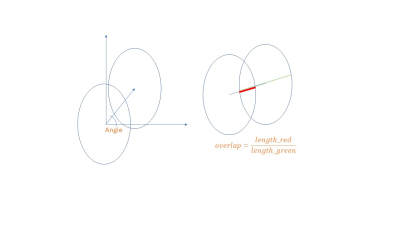
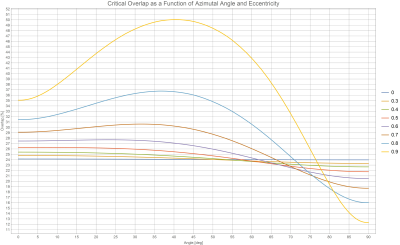
For two ellipses with a given eccentricity $$$e=\sqrt{1-\left (Min(a,b) /Max(a,b) \right )^2}$$$, we can define the new (more handy) overlapping coefficient $$$k'=1-1/k$$$ which is equal to the oblique overlapping length divided by the oblique diameter of the ellipse (Figure 1).
Based on the definition of Figure 1, we can minimize the functional from (1) as a function of the oblique overlap $$$k'$$$ and the angle between the two ellipses $$$α$$$ (Figure 2).
According to Figure 2 for two similar circles the overlapped coefficient is about 24% in any direction. For ellipses of great eccentricity (0.9), to achieve critical overlap under 40 deg one need to overlap them 50% of its oblique diameter.

Conclusions

The critical overlap between loops is a fundamental concept to consider when designing MRI receive coils. The diagram depicted in Figure 2 generalizes the well know result for circles [1] to ellipses of any eccentricity and can be useful for estimating overall dimensions of a uniform and isotropic array of ellipses.

Acknowledgements

We would like to express our special thanks to our colleague, Robert Stormont, for his vision and pioneering work leading to new kind of receive arrays.