Purpose

Conventional RF coil designs fail to produce uniform excitation across the brain at 7 Tesla due to the short wavelength of the B₁⁺ field. Furthermore, coil designs must account for field fluctuations due to subject to subject variation. Hardware adjustments that allow the shaping and control of Radio Frequency (RF) waves are therefore needed to enable robust imaging at 7 Tesla. RF shimming relies on modulating the amplitude and phase of each coil element in order to homogenize excitation over a slice or volume. Although previous work has shown RF shimming to be a promising technique for homogeneous excitation ^1–3, the efficacy of increased degrees of freedom, or more coil elements, in RF shimming is still an open question. With multi-channel systems and array power networks emerging in the field, it is important to establish how RF shimming alone performs with increased degrees of freedom over a range of realistic head models.

Methods

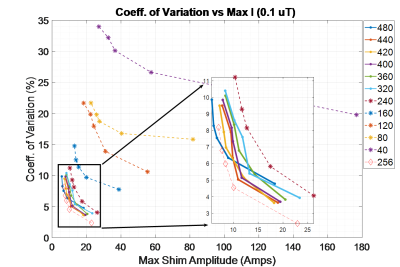
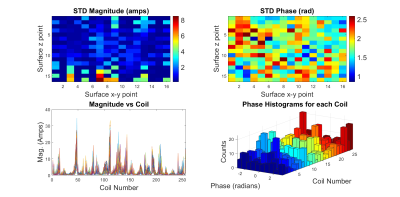
Initially, simulations using the finite difference time domain method were used to calculate electric and magnetic fields across the male National Library of Medicine (NLM) Visible Human Project® head model with 1 mm­ ³ isotropic spatial resolution and 29 tissue compartments ⁴. Using a transmission coil design of 1 cm radius copper loops placed on the surface of a 26.4 cm diameter cylinder, 480 (12 x 40 grid on the cylinder surface) individual loop elements’ field distributions were calculated across the head model. This grid of 480 was further sub-sampled row and column-wise into less dense arrays (see Fig. 1). The excitation profile was optimized over phase and amplitude of each coil element with intent to minimize the coefficient of variation of the B­₁⁺ magnitude across the brain’s volume while limiting power requirements. Starting at zero-target-phase across the volume, Tikhonov regularized optimization was performed iteratively, updating the target-phase pattern with the resulting phase generated by the shim weights every iteration until the cost function changed negligibly. The optimization simultaneously limits power and overcomes the non-convex nature of the optimization problem ⁵. The global specific absorption rate (SAR), local 10-gram average SAR, and transmit efficiency values were then calculated using the optimized shim field values. A separate geometry of 256-loops (16 x 16 staggered grid) centered on the brain region returned feasible excitation homogeneity under reasonable power constraints. This coil geometry’s shim weights were then optimized over 20 unique, 7 compartment, head models, at 3 (head angle) configurations within the coil to test performance against subject variation.

Results

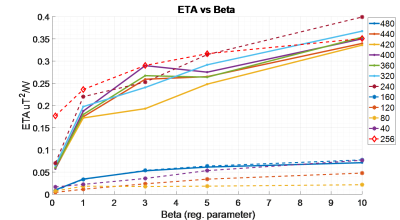
Considering a realistic power limitation on current amplitudes to each coil element (~12-20 amps), an array of 240-320 1 cm radius surface loops provides homogeneous excitation across the NLM Visible Human Project® brain volume with roughly 5% variation. A separate geometry of 256 elements centered around the brain performed best with a maximum local SAR of .0132 W/kg and global SAR of 8.6 µW/kg for a 90-degree, 0.1 µT target field (for a 1 µT hard pulse local and global SAR would be 1.32 W/kg and global SAR of .86 mW/kg). Transmit efficiency for the array ranged from 0.17 to 0.35 µT²/Watt. Coil geometries with columns of loops stacked along z, had roughly a 0.2 µT²/Watt increase in transmit efficiency in comparison to loops staggered on the surface of the cylinder or limited to rows in the x-y plane (see Fig. 2). Over 60 unique head configurations, the optimized shim weights confirm that the B­₁⁺ phase changes more drastically than the magnitudes in order to account for subject variability (see Fig. 3).

Discussion

These simulations are intended to direct the construction of a multi-surface-loop coil array with RF shim capabilities. The coil array will be driven by the Philips Multix8 Radio Frequency Power Amplifier (RFPA) system. A distribution network utilizing micro-strip Wilkinson power splitters will be combined with a butler matrix array connecting the coil array to the RFPAs. The butler matrix array will potentially simplify the number of channels required to achieve homogeneous excitation. Vector modulators will be used in order to control the amplitude and phase of each coil.

Conclusion

RF shimming combined with array networks to numerous coil elements may facilitate use of ultra-high field systems both for research and clinical applications. Subject to subject variation may be accounted for given the correct shim optimization. Theoretically, a 240 to 320 surface loop array provides enough degrees of freedom to tailor the field given appropriate decoupling and distribution networks.

Acknowledgements

The authors would like to acknowledge Bennett Landman and Benoit Dawant for preparing and providing the registered head model data along with Will Grissom and Xinqiang Yan for helpful discussions concerning coil design and shim optimization techniques. Research reported in this publication was supported by the National Institute of Health under award numbers R21 EB024311 and R01 NS095291.