4070
Routing algorithm for the interconnection of closed wire loops for MR gradient and MR shim coils
Philipp Amrein1, Feng Jia1, Sebastian Littin1, and Maxim Zaitsev1
1Dept. of Radiology, Medical Physics, University Medical Center Freiburg, Freiburg, Germany
1Dept. of Radiology, Medical Physics, University Medical Center Freiburg, Freiburg, Germany
Synopsis
An automatized solution is presented for the generation of a single wire track from closed loops for complex coil and supporting structure topologies. The algorithm includes a mesh parameterization, a toplogical analysis, route optimization between groups of loops and finally opening and interconnection of the loops.
Introduction
The boundary element method is a flexible technique for designing of shimming and gradient coils, which allows to find optimized current densities for given target fields on almost arbitrary meshed surfaces. 1 However, the resulting discretized wire tracks are are typically presented as closed loops. Therefore sequential routing and interconnection is required to obtain a single wire track which only then can be driven by a single current amplifier. In the past the loop interconnection procedure was done manually by the gradient designer. This limits the scope of problems since for complex layouts this design step might be demanding and time consuming. To solve this problem an automatized algorithm is presented which especially employs a mesh parameterization into a two-dimensional plane.Methods
The algorithm is composed of several steps including (i) mesh parameterization, (ii) discretization of the current density, (iii) loop evaluation, (iv) topological grouping, (v) route optimization, (vi) loop opening and finally (vii) interconnection to a single wire track. As a first step the triangulated current carrying surface (mesh) is parameterized into an equivalent planar representation. (See Fig 1) Here a discrete free‐boundary conformal parameterization is used. 2 This approach simplifies the following steps significantly by the reduction of one spatial dimension. Furthermore, the reversed transformation can be used to return to the curved three-dimensional surface. Thereafter, level lines of the stream function potential can be calculated in the planar domain. (See Fig 2) These closed planar loops represent the discrete current density and are topologically sorted as follows. The term "group" refers to a set of loops for which each loop is directly contained by one and only one of another loop of that set. A "level" is a set of parallel groups identically contained by the same group. The sorting of the full topology into groups of concentric loops is breaking down the problem into parts for which the interconnection is done accordingly. (See Fig 3) For a single group, the conventional interconnection method is used. Here the loops are being opened with a radial cut with predefined uniform width. The cut is aligned towards the center of the most inner loop. The loops are then interconnected end to start. The return path along the cut from the most inner to the outer loop will ensure cancellation of unwanted field that is introduced by the component of the loop interconnection. Among individual groups, the algorithm processes sets of parallel groups ("level). For each level, the start location is the cut of most inner loop of the respective enclosing group. The sequence of groups within a "level" is found by solving a routing problem for the positions of the center of masses of the individual groups. This approach is similar to the routing problem of the "traveling salesman" 3. If a level has no enclosing group, this level is seen as "top-level" and the overall wire start can be considered the start location. Traveling group to group is realized by splitting the most outer loop of each group into two parts. The first part can be employed to approach the next group in the level whereas the second part is used to construct an overall return path after every group has been included. The current orientation of groups are either clockwise or anti clockwise and can be estimated by analysis of the local gradient of the stream function potential. Since the wire track is constructed on the planar surface representation, a reverse transformation yields the associated track warped to the curved surface. As final step, a predefined conductor cross section is being swept along the wire track to create a realistic conductor volume. Here wire intersections with the return path are avoided by shifting the return paths along the normal of the curved surface.Results
The algorithm was written in MATLAB and has been tested and used in the development of a non-linear local gradient coil for diffusion weighting in breast imaging. (See Fig 1-5) For multiple slightly varying geometries for the current surfaces (different varieties of ´cup´-forms) the routing algorithm yielded corresponding wire tracks reliably. Magnetic gradient field calculation employing Biot-Savart law detected acceptable minor deviations under 5% compared to the magnetic field directly calculated from the stream function.Discussion
Since the algorithm allows fast generation of coil layouts within only few minutes on standard office-pc hardware, the rate of design iterations on the current carrying surface geometry can be significantly increased. However, since parameterization mappings for surface meshes are in general not unique, a reasonable choice must be made between isometric (length preserving), conformal (angle-preserving) and equiareal (area-preservings) mappings.Conclusion
For complex gradient and shim coil layouts 4 especially on complex supporting surfaces the presented algorithm may significantly accelerated the design process since it is not limited by topological complexity. Furthermore, the generated volumetric conductor may be used in realistic finite element simulations to further improve the reliability of the design process.Acknowledgements
- German Research Foundation (Grant Number ZA 422/5‐1)
References
- G.N. Peeren,Stream function approach for determining optimal surface
currents,Journal of Computational Physics,Volume 191, Issue
1,2003,Pages 305-321,ISSN
0021-9991,https://doi.org/10.1016/S0021-9991(03)00320-6.
- Mullen, P. , Tong, Y. , Alliez, P. and Desbrun, M. (2008), Spectral
Conformal Parameterization. Computer Graphics Forum, 27: 1487-1494. doi:10.1111/j.1467-8659.2008.01289.x
- Der Handlungsreisende wie er sein soll und was er zu thun hat, um Aufträge zu erhalten und eines glücklichen Erfolgs in seinen Geschäften gewiß zu sein ; Mit e. Titelkupf. / von einem alten Commis-Voyageur. - Ilmenau : Voigt, 1832
- Jia, F, Elshatlawy, H, Aghaeifar, A, et al. Design of a shim coil array matched to the human brain anatomy. Magn Reson Med. 2019; 00: 1– 16. https://doi.org/10.1002/mrm.28016
Figures
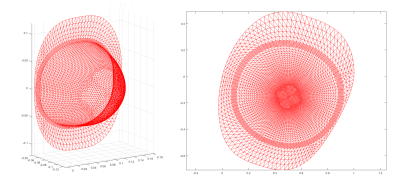
Figure 1: Triangulated representations of the current carrying surface for an example of the development of a non-linear local gradient coil for diffusion weighting in breast imaging. Left: Curved mesh, Right: Parameterized planar mesh.
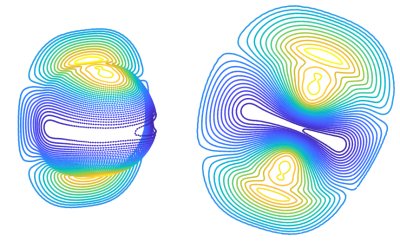
Figure 2: Contour lines of the stream function. The colors are defined by the stream function values on each loop. Left: Curved representation; Right: Planar representation. Note that small loops with average target gradient contribution below 1% have been automatically removed to simplify the layout.
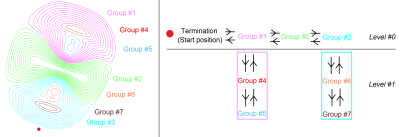
Figure 3: Left: Topologically grouped contour lines. The red dot indicates the given starting point for routing. Right: Routing diagram.
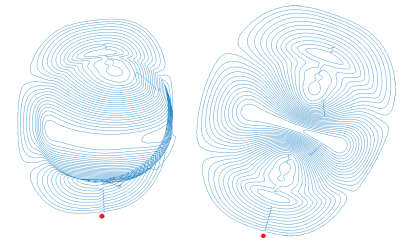
Figure 4: Resulting continuous wire track. Left: Curved surface; Right: Planar surface. The red dot indicates the location for the plug connection.
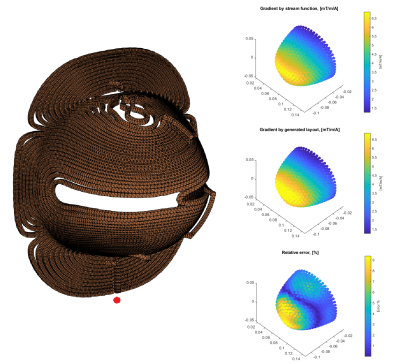
Figure 5: Left: Final volumetric conductor body with a rectangular cross section of 4mm. Note that return path intersections where avoided by shifting the overlapping wire along the normal of the curved surface. Right: Top: Gradient by the stream function, Right Middle: Gradient by the generated wire track, Right Bottom: Relative error (Difference in gradient divided by the maximum of the target gradient). The average relative error is 2% whereas the maximum relative error is 9.4% for a small frontal area .