3971
A Hierarchical Latent Space Network Model for Population Studies of Functional Connectivity1Mathematics and Statistics, University of San Francisco, San Anselmo, CA, United States, 2Political Science, The Ohio State University, Columbus, OH, United States, 3Center for Neuroscience and Department of Psychology, New York University, New York, NY, United States
Synopsis
Functional connectivity scans are hierarchical – heterogeneity differentiates people according to clinical diagnosis and stage of disease. Hierarchy furthermore dictates connectivity of an individual - functional networks manifest as a hierarchy of subnetworks, each with their own unique biological function. To model functional connectivity across populations of individuals, we develop the hierarchical latent space model (HLSM), a statistical model that accounts for hierarchy as a function of clinical and connectivity features describing functional images. The HLSM reveals differences in the connectivity patterns between healthy and schizophrenia groups when applied to data from the Center for Biomedical Research Excellence (COBRE) project.
Introduction
Initial attempts at discerning population- and individual-level hierarchies have focused on the analyses of activation motifs like clustering, overall connectivity, and network diameter1. A majority of techniques to study these features suffer from one of three major issues. First, methods often analyze single activation motifs in isolation2.. Activation motifs, however, are often highly correlated with one another, and thus may have unexpected interactions that are only apparent when considering multiple motifs simultaneously. Second, current techniques are often unable to separate the influence of activation motifs from the influence of anatomical properties. For example, the distance between nodes is often strongly related to connection strength and may confound attempts to quantify activation motifs3. Finally, most existing techniques provide a single point estimate of a parameter, making it difficult to compare that value against chance.These challenges necessitate the use of generative network models that not only jointly characterize the effect of the activation motifs on the structure of the brain, but also provide a measure of statistical certainty to the observed trend. Recent work has called for the use of such generative network models in structural and functional analyses4,5. Motivated by these challenges, we introduce a hierarchical network model that captures patterns in functional connectivity networks at both the individual and population level.
Methods
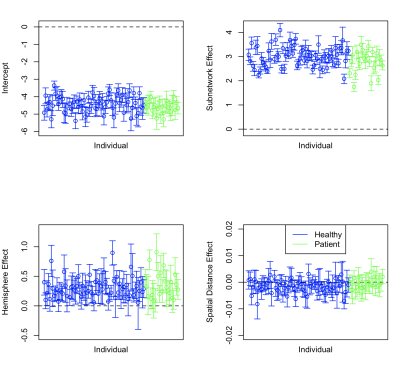
We introduce and investigate a generative network model, called the hierarchical latent space model (HLSM). The HLSM is a joint probability distribution that models the generative mechanism of a collection of connectivity networks arising in population studies as a function of observable covariates, which are common across individuals, as well as unobserved latent information that describes individual and population-level hierarchical structures. Our model quantifies both the effect of activation motifs as well as anatomical properties on the generative mechanism describing the brain. Through network models like the HLSM, we can formally test otherwise empirical findings like the small-world phenomenon.We apply the HLSM to a population of functional data from a group of 71 healthy individuals and a group of 24 patients with paranoid schizophrenia from the Center for Biomedical Research Excellence (COBRE) study. We consider three network-based features in our analysis: hemisphere location, subnetwork location, and spatial distance. The hemisphere location feature is a binary dyad- level variable that indicates whether or not a pair of nodes (regions) are located in the same hemisphere of the brain, either the left hemisphere, right hemisphere, or the midline. The subnetwork location is also a binary dyad-level variable that indicates whether or not two regions are located in the same known subnetwork. The spatial distance covariate describes the Euclidean distance between regions. Given that regions within a hemisphere are typically more connected within rather than across hemisphere6, we expected this covariate to be significantly positive. We furthermore expected that the spatial distance between two regions to be inversely related to their propensity to interact.
Results
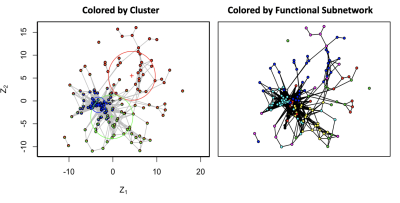
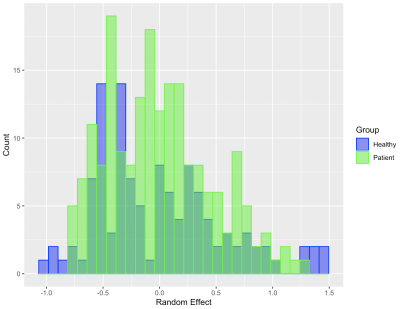
Our analysis reveals several important aspects of these groups. First, for both healthy and patient groups, the hemisphere and subnetwork location of two regions strongly influence their propensity to connect. We also find that alone, spatial distance between two regions is significantly and inversely related to their connection probability, but that it is no longer significant once hemisphere and subnetwork locations have been controlled for (Figure 1). Within-network clustering is also identified by the HLSM, and when accounted for, systematically outperform other covariate models when clusters do not confound with the included covariates (Figure 2). Finally, we find increased heterogeneity in the connectivity of the healthy group over the patient group which may explain less resilient connectivity patterns in patients with schizophrenia (Figure 3).Discussion
With the HLSM, we were able to formally test the effects of network motifs on functional connectivity. The findings in our study would not have been possible through typical separate analyses of activation motifs. Rather, joint probability models like the HLSM are required to fully characterize the marginal effects and interactions of activation motifs. These findings, produced in this way, have substantial implications for future research because very little of the existing literature on network neuroscience has made use of generative statistical models. A small portion of those studies that have have used models that account for the weighted structure of functional connectivity networks, and ours is the only one of which we are aware that allows for the explicit modeling of hierarchical structure - despite the fact that hierarchy is ubiquitous in neurological networks. As such, the HLSM is a technique that researchers can use to delve much deeper into the nature of functional connectivity networks than has previously been possible.Conclusion
Future research will investigate the development and implementation of other hierarchical models for functional connectivity studies. Our analysis of the population data in the COBRE data set suggests that the HLSM is able to identify patterns in functional connectivity that other network analyses would not have been able to identify. With generative models like the HLSM, we aim to fully understand the generative mechanisms describing commonly observed structures in the brain like community structure and the small-world property. We hope that the HLSM provides a starting-point for these endeavors.Acknowledgements
JDW was supported by NSF grant DMS-1830547. SJC was supported by NSF grants SES-1357622, SES-1461493, and SES-1514750, NIH R-34 DA043079, and the Alexander von Humboldt Foundation’s Fellowship for Experienced Researchers. ZLL was supported by NSF- SMA 1533500. The authors have intellectual property considerations for using cGERGM in a medical context. SJC, JDW, and ZLL are co-founders and equity holders in Cerenetics, Inc., a start-up company commercializing the technology described in this abstract.References
[1] Olaf Sporns. Networks of the Brain. MIT press, 2011.
[2] Mikail Rubinov and Olaf Sporns. Complex network measures of brain connectivity: uses and interpretations. NeuroImage, 52(3):1059–1069, 2010
[3] CJ Honey, O Sporns, Leila Cammoun, Xavier Gigandet, Jean-Philippe Thiran, Reto Meuli, and Patric Hagmann. Predicting human resting-state functional connectivity from structural connectivity. Proceedings of the National Academy of Sciences, 106(6):2035–2040, 2009.
[4] Richard F Betzel and Danielle S Bassett. Multi-scale brain networks. NeuroImage, 2016.
[5] Richard F Betzel and Danielle S Bassett. Generative models for network neuroscience: Prospects and promise. Journal of The Royal Society Interface, 14(136):20170623, 2017.
[6] Deepak N Pandya and Douglas L Rosene. Some observations on trajectories and topography of commissural fibers. Epilepsy and the corpus callosum, 21–39. Springer, 1985.
Figures