3930

Approaches for Modeling Spatially Varying Associations Between Multi-Modal Images
Alessandra Michelle Valcarcel1, Simon N Vandekar2, Tinashe Tapera3, Azeez Adebimpe3, David Roalf3, Armin Raznahan4, Theodore Satterthwaite3, Russell T Shinohara1, and Kristin A Linn1
1Penn Statistics in Imaging and Visualization Center, Department of Biostatistics, Epidemiology, and Informatics, University of Pennsylvania, Philadelphia, PA, United States, 2Department of Biostatistics, Vanderbilt University, Nashville, TN, United States, 3Department of Psychiatry, University of Pennsylvania, Philadelphia, PA, United States, 4Developmental Neurogenomics Unit, National Institute of Mental Health, Bethesda, MD, United States

Synopsis

Multi-modal MRI modalities quantify different, yet complimentary, properties of the brain and its activity. When studied jointly, multi-modal imaging data may improve our understanding of the brain. We aim to study the complex relationships between multiple imaging modalities and map how these relationships vary spatially across different anatomical brain regions. Given a particular location in the brain, we regress an outcome image modality on one or more other modalities using all voxels in a local neighborhood of a target voxel. We apply our method to study how the relationship between local functional connectivity and cerebral blood flow varies spatially.

Introduction

All current methods for imaging the brain and measuring its activity (structural magnetic resonance imaging (MRI), functional MRI, diffusion tensor imaging (DTI), computerized tomography (CT), positron emission tomography (PET), electroencephalogram (EEG), and more) have both technical and physiological limitations.1 Multi-modal imaging provides complementary measurements to enhance signal and our understanding of neurobiological processes.2 When studied jointly, multi-modal imaging data may improve our understanding of the brain. Unfortunately, the vast number of imaging studies evaluate data from each modality separately (voxel- or region-wise) and do not consider information encoded in the relationships between imaging types. Multivariate pattern analysis (MVPA) integrates information across a set of modalities that are predictive of a phenotype using models such as support vector machines (SVM)5, independent component analysis (ICA)6, or canonical correlation analysis (CCA)7. Although MVPA fuses information from multi-modal data in predictive settings, few studies utilize complementary multi-modal data to provide additional insight during population-level, voxel-wise analyses. An exception is biological parametric mapping (BPM)3,4 which allows for a voxel-wise regression of one image modality on another image and other covariates of interest. In this work, we include local spatial information in voxel-wise analyses by rigorously accounting for the dependence structure when characterizing associations between image modalities. We call our framework inter-modal coupling (IMCo) and propose several approaches to estimate the IMCo model parameters that account for the spatial dependence among voxels. We then use IMCo to study the relationship between local functional connectivity and cerebral blood flow.

Methods

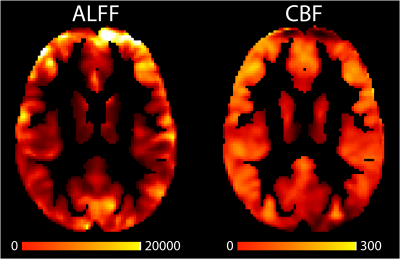
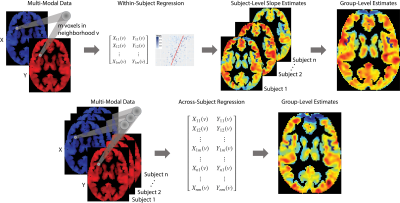
We apply our framework to the Philadelphia Neurodevelopmental Cohort (PNC), a large-scale (n = 1601), single-site study of brain development in adolescents.8 We analyze 831 adolescents (478 females) aged 8-23 (mean=15.6; sd=3.36) who completed neuroimaging as part of the PNC and passed imaging quality assurance procedures. To study the relationship between local functional connectivity and cerebral blood flow we use amplitude of low frequency fluctuations (ALFF) and cerebral blood flow (CBF) imaging modalities. ALFF quantifies the amplitude of low frequency oscillations over time and space from resting-state BOLD scans to determine correlated activity between brain regions. CBF was calculated from brain perfusion imaging using a custom written pseudo-continuous arterial spin labeling (pCASL) sequence.9 Figure 1 shows example axial slices of ALFF and CBF images.

We aim to study the relationship between ALFF and CBF throughout the brain and map how the relationship varies spatially across different anatomical regions by regressing ALFF on CBF. Let $$$v$$$ denote a specific voxel in the brain, where $$$v = 1,…,V$$$ indexes all voxels in the gray matter. Given a particular location in the gray matter $$$v$$$, we regress the outcome image modality (ALFF) on the remaining modality (CBF) using data from all voxels in a local neighborhood of the target voxel $$$v$$$. We call the spatially varying relationship between two imaging modalities inter-modal coupling (IMCo), which can be estimated at the subject (within-subject) or population (across-subject) level. Figure 2 describes the within- and across-subject coupling frameworks.

Using the PNC, we compare the performance of three estimation frameworks that account for the spatial dependence among voxels in a neighborhood $$$v$$$:

  1. generalized linear models (GEE)
  2. linear mixed effects models (LME)
  3. weighted least squares models (WLS) using either within-subject or across-subject estimation

We are interested in the population-level average change in ALFF due to a unit change in CBF at a target voxel $$$v$$$. That is, we are interested in the slope ($$$\beta_1$$$) of the linear relationship between ALFF and CBF, which we refer to as the IMCo slope. The GEE approach permits a marginal interpretation of the IMCo slope estimate, while the estimates from the LME model and WLS approach have a conditional, i.e., subject-specific, interpretation.

In this analysis we simply use a single imaging modality as a predictor (CBF) but extensions can include more complementary imaging modalities and subject-level covariates. These IMCo modeling approaches all relate information from complementary modalities while accounting for the spatial dependence of voxels in neighborhood of a target voxel in order to provide insight about how variation in cerebral blood flow relates to the strength of local functional connectivity throughout the brain.

Results

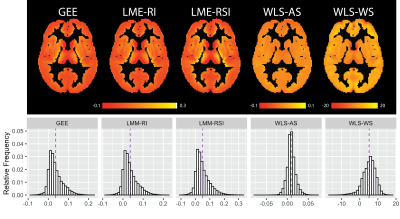
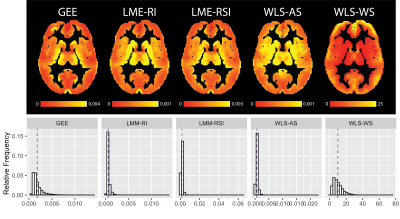
The example axial slice and histograms provided in figure 3 show the population-level analysis using across-subject estimation results in almost identical IMCo slope ($$$\beta_1$$$) estimates at the voxel level for the GEE and LME models. Both WLS approaches (across- and within-subject) differ from the GEE and LME model. The histograms in figure 3 show the WLS estimates are larger than those coming from the GEE and LME models.

Using the maps and histograms presented in figure 4 the standard error estimates associated with the IMCo slope ($$$SE(\beta_1)$$$) maps differ significantly across all the estimation procedures.

Discussion

Inter-modal coupling (IMCo) provides a framework to study the complex relationships between multiple imaging modalities. While the population-level IMCo slope ($$$\beta_1$$$) estimates are similar across estimation procedures the standard error estimates for the IMCo slope ($$$SE(\beta_1)$$$) differ for each estimation approach. The variable standard error estimates across estimation procedures leads to different conclusions during inference. Future work will include using IMCo to investigate structure-function relationships in neurodevelopment, aging, and pathology.

Acknowledgements

This work was supported by the National Institutes of Health R01MH112847 and R01NS060910. A.R was supported by was supported by the intramural program of the National Institutes of Health (Clinical trial reg. no. NCT00001246, clinicaltrials.gov; NIH Annual Report Number, ZIA MH002949-03). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agency.

References

1. Liu S, Cai W, Liu S, et al. Multimodal neuroimaging computing: A review of the applications in neuropsychiatric disorders. Brain Inform. 2015;2(3):167-180. doi:10.1007/s40708-015-0019-x

2. Biessmann F, Plis S, Meinecke FC, Eichele T, Müller K-R. Analysis of multimodal neuroimaging data. IEEE Rev Biomed Eng. 2011;4:26-58. doi:10.1109/RBME.2011.2170675

3. Casanova R, Srikanth R, Baer A, et al. Biological parametric mapping: A statistical toolbox for multimodality brain image analysis. NeuroImage. 2007;34(1):137-143. doi:10.1016/j.neuroimage.2006.09.011

4. Yang X, Beason-Held L, Resnick SM, Landman BA. Biological Parametric Mapping WITH Robust AND Non-Parametric Statistics. NeuroImage. 2011;57(2):423-430. doi:10.1016/j.neuroimage.2011.04.046

5. Zhang D, Wang Y, Zhou L, Yuan H, Shen D. Multimodal classification of Alzheimer’s disease and mild cognitive impairment. NeuroImage. 2011;55(3):856-867. doi:10.1016/j.neuroimage.2011.01.008

6. Calhoun VD, Liu J, Adali T. A review of group ICA for fMRI data and ICA for joint inference of imaging, genetic, and ERP data. NeuroImage. 2009;45(1 Suppl):S163-172. doi:10.1016/j.neuroimage.2008.10.057

7. Correa NM, Li Y-O, Adalı T, Calhoun VD. Canonical Correlation Analysis for Feature-Based Fusion of Biomedical Imaging Modalities and Its Application to Detection of Associative Networks in Schizophrenia. IEEE J Sel Top Signal Process. 2008;2(6):998-1007. doi:10.1109/JSTSP.2008.2008265

8. Satterthwaite TD, Elliott MA, Ruparel K, et al. Neuroimaging of the Philadelphia Neurodevelopmental Cohort. NeuroImage. 2014;86:544-553. doi:10.1016/j.neuroimage.2013.07.064

9. Wu W-C, Fernández-Seara M, Detre JA, Wehrli FW, Wang J. A theoretical and experimental investigation of the tagging efficiency of pseudocontinuous arterial spin labeling. Magn Reson Med. 2007;58(5):1020-1027. doi:10.1002/mrm.21403

Figures

Example axial slices of ALFF and CBF images are provided. The brain mask includes voxels within the gray matter (minimum 10% probability according to an atlas prior) that had adequate image coverage for both rsfcMRI and ASL.

An example of within-subject (row 1) and across-subject (row 2) coupling frameworks are provided. We let $$$j = 1,…,m$$$ denote voxels within the neighborhood of the target voxel $$$v$$$. Within-subject coupling is implemented by weighted least squares regression (WLS) whereas across-subject coupling is implemented using generalized estimating equations (GEE), linear mixed effects models (LME), and WLS approaches.

An axial slice of the estimated population-level slope ($$$\beta_1$$$) maps from each modeling procedure are presented (row 1). The range of the maps across estimation procedures differs. Therefore, GEE, LME-RI, and LME-RSI share a color bar while WLS-AS and WLS-WS maps have separate color bars to relate color and intensity. For each estimation procedure, we include histograms generated using all voxel intensities in the brain (row 2). The mean $$$\beta_1$$$ intensity for each respective estimation approach is highlighted by the dashed purple vertical line.

An axial slice of the population-level slope standard error ($$$SE(\beta_1)$$$) maps from each modeling procedure are presented (row 1). The range of the maps across estimation procedures differs. Therefore, each estimation procedure has a unique color bar to relate color and intensity. For each estimation procedure, we include histograms generated using all voxel intensities in the brain (row 2). The mean $$$SE(\beta_1)$$$ for each respective estimation approach is highlighted by the dashed purple vertical line.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3930