3870
7T EPI Nyquist Ghost Reduction by Combining Trajectory Measurement, Navigator Echoes and an Inverted Readout Polarity Calibration Scan1Wellcome Centre for Human Neuroimaging, UCL Queen Square Institute of Neurology, UCL, London, United Kingdom
Synopsis
A combination and development of several existing calibration and reference techniques for Nyquist ghost reduction allowing 2D EPI fMRI images to be reconstructed with very low ghost level at 7T in demanding gradient regimes.
Introduction
When EPI fMRI is performed at 7T rapid signal decay in grey matter necessitates short TE for optimum BOLD sensitivity. This can be achieved by minimising the echo-spacing of the EPI readout. However, this is demanding on gradient performance and can lead to significant deviation from the expected k-space trajectory, eddy current formation, mechanical vibration, and consequently stronger Nyquist ghosting. B0 shim is also challenging at 7T with off-resonance effects further amplifying Nyquist ghost levels1. Ghosts reduce functional sensitivity and specificity by displacing signal from its true position. Where ghosts overlap with the main image, functional sensitivity can be severely reduced if participant motion perturbs the overlapping interference pattern over time.Methods
In the present work we have combined and developed several existing calibration and reference techniques for Nyquist ghost reduction.Firstly, on a periodic basis, we perform a robust trajectory measurement2 to measure the EPI readout gradient waveform using a gel phantom3. We found stable results (Fig. 1) across different scanning sessions and days. From these data we compute a generalised readout direction Fourier reconstruction matrix4 which is applied to ongoing EPI.
Secondly, three conventional alternating-polarity navigator echoes5 are acquired at short TE, prior to the main EPI readout. Although alone, at 7T, these provide only partial Nyquist ghost reduction, they can compensate for time-dependent variation occurring with respect to the initial calibration scan, e.g. temperature6 or participant motion (such as breathing). For our proposed correction, navigator measurements from an early volume serve as the baseline.
Thirdly, at the start of each functional run we acquire a single volume calibration scan with opposite readout gradient polarity to what is being used to acquire the time series. We follow the approach of Chen and Wyrwicz7. Appropriate lines are selected from the calibration volume, and from the first normal polarity volume to reconstruct two volumes formed under solely negative and solely positive gradients respectively, and the 3D phase difference map between the two (Fig. 2). Each on-going EPI image is then reconstructed analogously into pairs of images each with half the target field-of-view (since taking only half the readouts leaves the data two-fold under-sampled). A full-field-of-view image is computed by solving simultaneously, at each location in the half-field-of-view, for the pair of full-FOV voxel values that best fit the under-sampled images, given the phase difference map. This is described in ref. 7, equations 8 and 9, with a caveat that fitting is under-determined where only one of the voxel pair lies within the object. We recast the problem in a linear modelling framework, which can be augmented with Tikhonov regularisation for improved stability. Following their definitions of variables and with our regularisation term $$$\Lambda(x,y)$$$$$\left(\begin{array}{c}EPI_{odd}(x,y)\\ EPI_{even}(x,y)\\ 0\\0\end{array}\right)=\left(\begin{array}{c}\frac{1}{2} & \frac{1}{2}\\ \frac{1}{2}exp(i\theta(x,y)) & -\frac{1}{2}exp(i\theta(x,y-\frac{FOV}{2})) \\ \Lambda(x,y) & 0 \\ 0 & \Lambda(x,y-\frac{FOV}{2})\end{array}\right)\left(\begin{array}{c}\tilde{M}(x,y)\\ \tilde{M}(x,y-\frac{FOV}{2})\end{array}\right)+ \left(\begin{array}{c}\\ \epsilon \\\ \end{array}\right)$$where$$$\Lambda(x,y)=\frac{\lambda}{\sqrt{smooth(\sum_{coil}Regrouped_2Regrouped_2^*)}}$$$, $$$\epsilon$$$ represents an error term in the linear model and $$$smooth()$$$ represents 3D convolution.
In the case of minimal variation in the phase-encoded direction (here anterior-posterior, Fig.2b), the calibration can be collapsed by taking the mean. Without requiring a linear modelling approach, the mean phase (Fig.2a) can then be applied to one of the half-FOV images before recombination with the other giving a simpler reconstruction (referred to as "2D phase correction" below).
The method was implemented in Matlab8 using Gadgetron9 to enable real-time operation at the scanner.
In vivo data were acquired on a Siemens 7T Terra with the following key parameters: TE=35ms, TR=75ms, 108 x 96 voxels x 96 slices, 2mm isotropic resolution. The same in-house 2D-EPI sequence used to acquire task-free fMRI data was adapted to enable trajectory measurement and negative polarity calibration scan. To investigate the interaction of ghosting levels with gradient requirements10, two datasets were acquired with different echo-spacing of 530 or 550us respectively.
Results
Figures 3 and 4 demonstrate the inverted polarity pre-calibration measurement even with our simpler 2D phase correction dramatically reduces the ghosting, at both echo-spacings (Figs.3c, 4c).Discussion
We have observed significantly reduced ghosting levels in 2D-EPI at 7T by measuring and accounting slice-wise for imperfections in gradient performance. Timing and waveform errors are measured via trajectory calibration2, which is stable over time and imaging sessions. The session-specific calibration scan provides spatial information about the imperfections. In combination, correcting for both effects greatly reduces the ghosts that manifest in the time series.The limited benefit of the conventional three navigator echoes may reflect sensitivity to short-term eddy current effects no longer present at the echo time of the EPI readout. However, this information can be beneficial when used to track changes with respect to the time at which the calibration data were acquired.
Our approach to average the 3D phase difference map in the phase encoded direction yields a simpler 2D phase correction that effectively suppresses ghosts. This simpler correction is intrinsically well conditioned and shares a consistent TE with the ongoing data acquisition and is robust against poor shim, unlike previously proposed "blip-off" pre-scans11 which will inherently average across a range of phase dispersion that can lead to signal cancellation.
Conclusions
The presented method allows 2D EPI fMRI images to be reconstructed with very low ghost level at 7T in demanding gradient regimes.Acknowledgements
The Wellcome Centre for Human Neuroimaging is supported by core funding from the Wellcome Trust [203147/Z/16/Z].References
- van der Zwaag W, Marques JP, Lei H, Just N, Kober T, Gruetter R. Minimization of Nyquist ghosting for echo-planar imaging at ultra-high fields based on a"negative readout gradient" strategy. J Magn Reson Imaging. 2009Nov;30(5):1171-8.
- Zhang Y, Hetherington HP, Stokely EM, Mason GF, Twieg DB. A novel k-space trajectory measurement technique. Magn Reson Med. 1998 Jun;39(6):999-1004.
- www.goldstandardphantoms.com/funstar
- Josephs O, Deichmann R, Turner R,Trajectory measurement and generalised reconstruction in rectilinear EPI,NeuroImage, Volume 11, Issue 5, Supplement, 2000, Page S543
- Schmitt, F., Stehling, M. K., & Turner, R. (1998). Echo-Planar Imaging. Berlin: Springer.
- Stich M, Pfaff C, Wech T, Slawig A, Ruyters G, Dewdney A, Ringler R, KöstlerH. Temperature-dependent gradient system response. Magn Reson Med. 2019 Oct 8.doi: 10.1002/mrm.28013. [Epub ahead of print]
- Chen NK, Wyrwicz AM. Removal of EPI Nyquist ghost artifacts with two-dimensional phase correction. Magn Reson Med. 2004 Jun;51(6):1247-53.
- https://www.mathworks.com/
- Hansen MS, Sørensen TS. Gadgetron: An Open Source Framework for Medical Image Reconstruction. Magn Reson Med. 2013 Jun;69(6):1768-76.
- https://layerfmri.com/2017/11/27/how-to-deal-with-ghosts-in-high-res-epi/
- Bruder H, Fischer H, Reinfelder HE, Schmitt F. Image reconstruction for echoplanar imaging with nonequidistant k-space sampling. Magn Reson Med. 1992Feb;23(2):311-23.
Figures
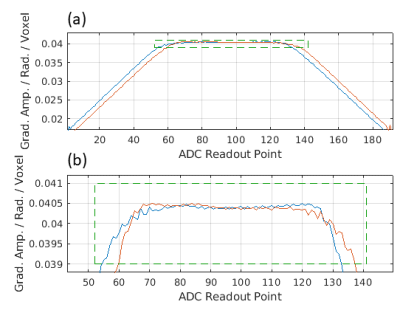

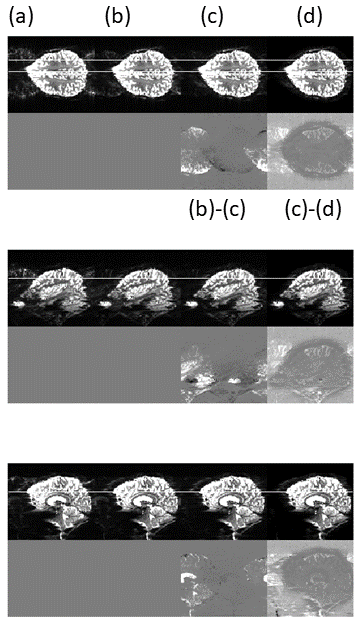
Figure 3. Reconstructed images with echo spacing 530us. Main images: left to right: (a) 3 navigator echo correction with vendor-standard assumed perfect trajectory; (b) 3 nav. with measured trajectory; (c) proposed "2D phase correction" with calibration data averaged in phase encoded (AP) direction; (d) proposed 3D correction - regularised 2D Nyquist ghost correction. Pairwise difference images: (b)-(c) and (c)-(d). High ghosting levels are seen in images reconstructed using the standard reconstruction provided by the vendor.

Figure 4. Echo spacing 550us . Image ordered as in Figure 3. The ghosts are somewhat reduced by replacing the idealised trajectory with that measured on the phantom (b). Additional gains are seen when using the 3D correction (d). However, this approach is sensitive to the choice of regularisation parameter, which may be undesirable for functional imaging.