3869
Multiple Orthogonal Reference Sensitivity Encoding Combined Over Dominant Eigencoils (MORSE CODE): Motion robust accelerated fMRI
Oliver Josephs1, Nadege Corbin1, Isobel Green2, Jonathan Roiser2, and Martina Callaghan1
1Wellcome Centre for Human Neuroimaging, UCL Queen Square Institute of Neurology, UCL, London, United Kingdom, 2Institute of Cognitive Neuroscience, UCL Queen Square Institute of Neurology, UCL, London, United Kingdom
1Wellcome Centre for Human Neuroimaging, UCL Queen Square Institute of Neurology, UCL, London, United Kingdom, 2Institute of Cognitive Neuroscience, UCL Queen Square Institute of Neurology, UCL, London, United Kingdom
Synopsis
Motion-robust reconstruction using a regularised SENSE-based unfolding of 3D-EPI time series for fMRI.
Introduction
Accelerated imaging requires coil sensitivity information for full-field-of-view images to be reconstructed from under-sampled data. The SENSE1 framework provides optimal SNR but requires accurate coil sensitivities supporting the full extent of the imaged object - meaning that the sensitivities ought to extend beyond the participant's initial position, e.g. to allow for motion during an fMRI time series. For accelerated fMRI it is common2,3,4 to measure coil sensitivity by acquiring an initial multi-shot calibration scan with identical readout timing as the under-sampled time series so as to match field-of-view and imperfections e.g. Nyquist Ghosting, distortion and drop-out. Initial coil sensitivity estimates derived from these data are often smoothed based on the assumption that the true coil profiles will be smooth, and to interpolate and extrapolate into regions where little or no signal is available, e.g. where poor B0 shim causes EPI signal amplitude reduction, or if the subject's position changes with respect to its position during the acquisition of calibration data. In certain regions image phase varies rapidly due to local susceptibility discontinuities e.g. orbital-frontal cortex and near the eyes. In the absence of a complex reference image, e.g. from a body coil, participant-specific phase variation remains and smoothing can result in signal loss due to phase cancellation, which in turn leads to errors during unfolding. This is a particular issue at ultra high fields, which typically lack a body coil. We have addressed this problem by a novel extension to the SENSE approach with multiple facets: (i) smooth sensitivity estimation with respect to multiple complex eigencoil references (in place of a single reference); (ii) SENSE reconstruction of multiple eigencoil images, regularised to suppress signal from unsupported regions; (iii) image combination across the different reference coil reconstructions in a manner analogous to GRAPPA5.Methods
Theory: Fully sampled calibration data are decomposed into eigencoils using singular value decomposition:[U, S, V] = svd(W), where W is an NxM matrix formed from the reference data; N=number of voxels, and M=number of receiver coils. Scaled eigencoils are obtained, E=U*S.
A subset of eigencoils, Eref with largest singular values are selected as references (Figure 1). Smoothed sensitivity is estimated by spatially locally fitting all eigencoils onto the principal reference eigencoils. Computationally, a least squares smooth sensitivity estimate, for each E (indexed by c) and for each Eref (indexed by r) can be efficiently obtained over the entire volume:$$\frac{smooth(E_c^{\star} {Eref_r})}{smooth(Eref_r^{\star} Eref_r)}$$where $$$smooth()$$$ can be fast, FFT-based, Gaussian spatial smoothing.
SENSE pseudo-inverse unfolding matrices are prepared, with Tikhonov regularisation terms:$$\Lambda = \frac{\lambda}{\sqrt{smooth(Eref_r^{\star} Eref_r))}}$$to suppress ill-conditioned reconstruction of signal in regions where $$$Eref_r$$$ has low amplitude.
Unfolding is applied to all under-sampled volumes to form multiple Eref-weighted images at each time point which are then combined by sum-of-squares.
Data Acquisition: The data used were acquired on a participant of a study into shock avoidance and therefore represent the higher end of motion that can be expected to occur in typical neuroimaging studies (of order several mm). The data were acquired at 3T with 1.5mm isotropic resolution using a full brain 3D-EPI sequence with factor 2 under-sampling in each phase-encoded direction using CAIPIRINHA sampling4. The data were reconstructed with either the proposed method (with 5 reference eigencoils), or regularised SENSE (with a sum-of-squares reference)2.
Reconstruction Implementation: The method was implemented in Matlab6 using Gadgetron7 to enable real-time operation at the scanner.
Results
Figure 1 shows five reference eigencoils and corresponding reconstructed images alongside a sum-of-square combination for comparison. Figure 2 compares one time point from the fMRI time series reconstructed with and without MORSE CODE, and with two levels of sensitivity smoothing. At this point during the functional run, the participant had moved by approximately 3mm with respect to their position during the acquisition of the calibration data. In the presence of motion high tSNR was only achieved when using a large sensitivity smoothing kernel in combination with the proposed MORSE-CODE approach. Figure 3 presents tSNR maps for each method, with a quantitative summary in figure 4 demonstrating a 47% improvement in tSNR when a broad smoothing kernel (FWHM of 4.5mm) was used to accommodate participant motion during the run.Discussion
While a FWHM of 4.5 mm would not be considered large in typical fMRI post-processing pipelines, the key difference here is that it is being applied to complex data making the sensitivity estimation highly vulnerable to errors in regions of high phase variation occurring over the length scale of the smoothing kernel. Our proposed method, which provides multiple, complex, reference coils with respect to which image domain coil sensitivities can be estimated, reduces the impact of large phase variation such as occurs in regions of poor shim. This allows larger smoothing kernels to be used and provides enhanced robustness to participant motion during fMRI time series. Five reference eigencoils were found to adequately support whole brain acquisitions at 3T.Conclusion
We have presented a motion-robust approach to regularised SENSE-based unfolding of 3D-EPI time series for fMRI. The approach produces high tSNR, a proxy for functional sensitivity, even when there is large motion between the acquisition of the initial calibration data and the ongoing acquisition of under-sampled data.Acknowledgements
The Wellcome Centre for Human Neuroimaging is supported by core funding from the Wellcome Trust [203147/Z/16/Z].References
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivityencoding for fast MRI. Magn Reson Med. 1999 Nov;42(5):952-62.
- Lin FH, Huang TY, Chen NK, Wang FN, Stufflebeam SM, Belliveau JW, Wald LL,Kwong KK. Functional MRI using regularized parallel imaging acquisition. MagnReson Med. 2005 Aug;54(2):343-53.
- Lutti A, Thomas DL, Hutton C, Weiskopf N. High-resolution functional MRI at 3 T: 3D/2D echo-planar imaging with optimized physiological noise correction. Magn Reson Med. 2013;69(6):1657–1664.
- Narsude M, Gallichan D, van der Zwaag W, Gruetter R, Marques JP. Three-dimensional echo planar imaging with controlled aliasing: A sequence for high temporal resolution functional MRI. Magn Reson Med. 2016 Jun;75(6):2350-61.
- Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B,
Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA).
Magn Reson Med. 2002 Jun;47(6):1202-10.
- https://www.mathworks.com/
- Hansen MS, Sørensen TS. Gadgetron: An Open Source Framework for Medical Image Reconstruction. Magn Reson Med. 2013 Jun;69(6):1768-76.
Figures
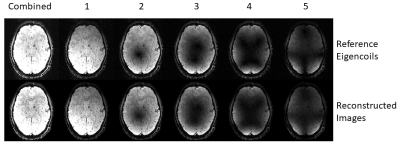
Figure 1. Dominant eigencoil references and associated reconstructed images.
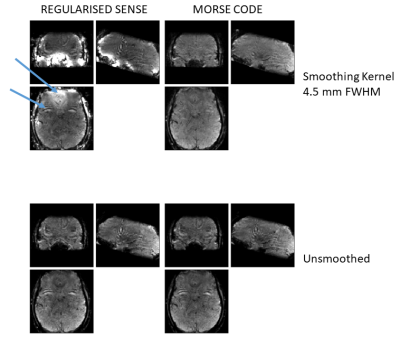
Figure 2. Regularised SENSE and MORSE CODE reconstructed images. Upper arrow highlights hyperintensity arising from smoothing over phase varying reference data in the orbito-frontal cortex. Lower arrow indicates large artefact originating from the eyes can be seen in its corresponding alias location in frontal cortex. This artefact is removed by combining MORSE-CODE with a larger smoothing kernel.
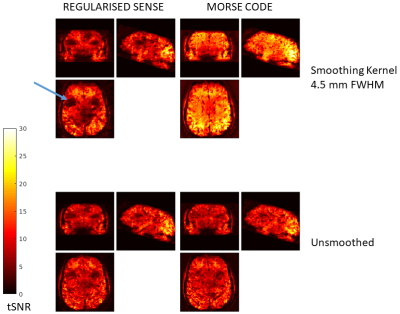
Figure 3. tSNR maps for SENSE and MORSE CODE. Note the aliased eye artifact in Figure 2 causes a severe reduction in tSNR from incorrect unfolding which is greatly improved by MORSE CODE with sensitivity smoothing.
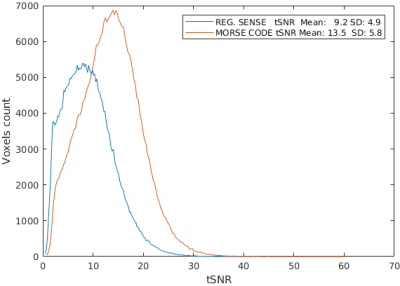
Figure 4. Histograms of tSNR for SENSE (blue) and MORSE CODE (red) reconstructions. Both employ a sensitivity smoothing kernel of 4.5 mm FWHM, i.e. corresponding to the upper row in Figures 2 and 3.