Introduction

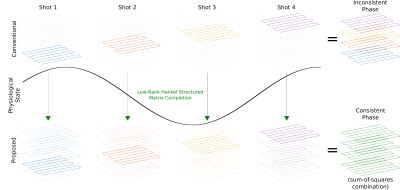
Three-dimensional multi-shot data acquisition is an effective way to provide high isotropic spatial resolution for fMRI^1. However, physiological fluctuations like respiratory motion during the acquisition of multi-shot segmented k-space can induce temporally varying phase across different shots, which results in phase cancellation and ghosting artifacts for each frame, leading to a decrease of tSNR and image quality^2,3. This can be particularly challenging for data acquisition at ultra-high field, and in lower brain regions, where respiratory-induced phase effects are strongest. In this study, we aim to solve this problem by using annihilating filter-based Hankel structured low-rank matrix completion^4,5, in which no explicit knowledge about the physiologically induced phase variation is necessary. Improved robustness and temporal stability are demonstrated compared to conventional multi-shot reconstructions.

Methods

We formulate our 3D reconstruction problem based on the 2D annihilating filter-based Hankel-structured low-rank matrix completion methods ALOHA⁴ and MUSSELS⁵. The existence of an annihilation relation is shown in the equations:
$$M(x)_{i}\cdot{}\Phi(x)_{j}-M(x)_{j}\cdot{}\Phi(x)_{i}=0\text{ (1)}\\
M(k)_{i}\ast{}\Phi(k)_{j}-M(k)_{j}\ast{}\Phi(k)_{i}=0\text{ (2)}$$
Where $$$M_{i}=M\cdot{}\Phi_{i}$$$, $$$\Phi_{i}$$$ is the physiologically induced phase for the i_th shot, $$$M$$$ is the complex image without phase corruption. From Eq. 2, the matrix generated from the concatenation of k-space Hankel matrices associated with each shot should be low rank, assuming the physiologically-induced phase is spatially smooth. This enables us to recover or interpolate the missing k-space values of each shot using a low-rank matrix completion algorithm.

As the number of shots in a 3D EPI acquisition can be high, we bin multiple shots into a smaller number of respiratory states according to respiratory information acquired from a respiratory bellows or internal navigator. This exploits the fact that respiration induced phase variation is nearly periodic, and reduces the dimensionality of the problem. Reconstruction is performed using a constrained optimisation:
$$ argmin_{X}=||E\cdot{}X-Y||_{2}^{2}\\
\text{s.t. }rank(H\cdot{}X)=r\\
\text{and }H\cdot{}X\text{ is Hankel structured}$$
Where X is the multi-state k-space and Y is the measured multi-shot k-space data. The encoding matrix E performs the composition of the following operators: M·F·S·F'·G', where G is the linear operator that sorts the shots into different physiological-states, M selects only acquired k-space locations for each shot, S represents multiplication by coil sensitivities, and F and F' are the forward and inverse Fourier transform respectively. H·X constructs the Hankel matrix from multi-state k-space data. This is solved using an alternating projection method⁶, cycling through the projections operations: (i) onto the data consistency set, (ii) onto the set of rank $$$r$$$ matrices, and (iii) onto the set of Hankel matrices. Once the multi-state k-space is interpolated and inverse Fourier transformed, the image is reconstructed using a sum-of-squares combination across states, which is insensitive to any inter-shot phase variation. In the conventional reconstruction, the multi-shot k-space is simply inverse Fourier transformed (Fig. 1). This procedure is applied independently to each time-point.

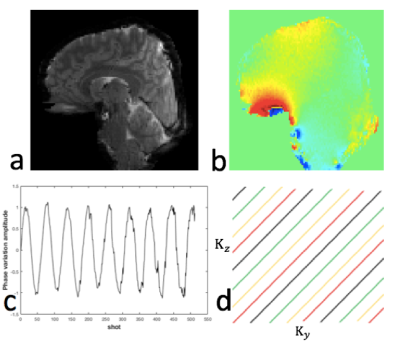
We validated this approach using realistic simulations based on a set of 3T data acquired with 2x2x1.5 mm³ resolution using a 64-channel receive coil. We applied a periodically varying linear phase in the superior-inferior direction, at low and high temporal variances. The max off-resonance of the added phase variation assuming TE=30ms was 1.4Hz (low variation) and 5.7Hz (high variation) . Then we synthesized the data at the acquired k-space locations for each shot with added complex noise. An inverse Fourier transform was performed first along Kx and each 2D Ky-Kz slice was processed separately. Reconstructions were performed with rank threshold 65 and kernel size 10, for 50 iterations. The sampling patterns and ground truth data are shown in Fig. 2. Segmented sampling with a ∆=1 CAIPI shift was used so every consecutive 24 shots had nearly uniform 3D k-space coverage. We simulated a 96 shot, 32-time-point high-resolution 3D EPI acquisition with binning of shots across 4 respiratory states, and evaluated the reconstruction performance by examining tSNR compared to a conventional reconstruction.

Results

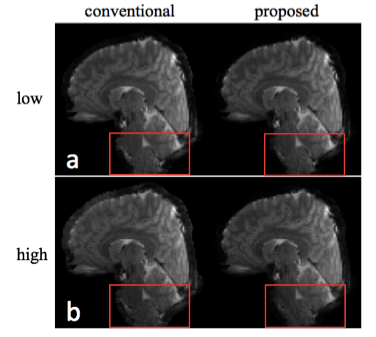
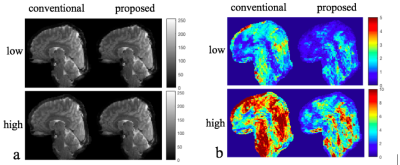
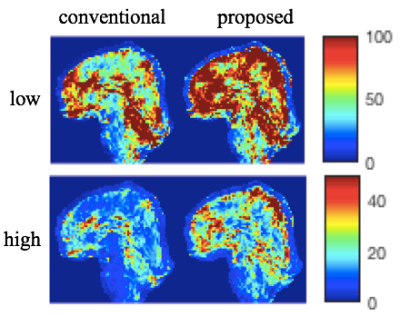
Fig. 3 shows representative magnitude images for both low and high temporal phase variations reconstructed with the conventional and the proposed method. In contrast to the phase variations induced by multi-shot diffusion encoding, physiologically induced phase variability does not result in obvious artifacts, although subtle ghosting can be observed.
Separate temporal mean and standard deviation images are shown in Fig. 4, for low and high phase variation. We see that the mean images are very similar, while the standard deviation images show marked reduction for the proposed method. In Fig. 5, tSNR is shown as the ratio of the temporal mean and standard deviation images, highlighting improved tSNR in the proposed method, due to reduced sensitivity to inter-shot phase errors. The improvement is particularly high in inferior regions that would be more sensitive to respiratory-induced phase, like the brain-stem and cerebellum. The mean tSNR improvement between proposed and conventional reconstruction across the whole brain is 43.2% for the low phase variation case, 51.6% for the high case.

Conclusion

The proposed method uses recently developed annihilating filter low-rank interpolation methods to improve the tSNR of multi-shot 3D EPI data. As multi-shot 3D acquisitions are increasingly being used, particularly for ultra-high resolution fMRI at ultra-high field strengths, reducing susceptibility to inter-shot physiological variations will be a key step towards robust, high fidelity 3D multi-shot fMRI.

Acknowledgements

The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). MC and WW are supported by the Royal Academy of Engineering (RF201617\16\23, RF201819\18\92).