3862
High SNR and High-Resolution fMRI using 3D OSSI and Tensor Model Reconstruction1Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, MI, United States, 2Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States
Synopsis
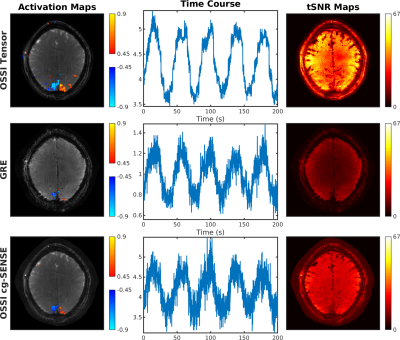
The goals of fMRI acquisition methods include high spatial and temporal resolutions with high signal to noise ratio (SNR). Oscillating Steady-State Imaging (OSSI) is a new fMRI acquisition method that provides large signals with high SNR, but may result in a slower acquisition of modest spatial resolution. This work improves OSSI spatial and temporal resolutions by exploiting the inherent high-dimensional structure of OSSI data and developing a tensor low-rank model for OSSI prospectively undersampled reconstruction. Compared to GRE imaging with the same spatial-temporal resolution, 3D OSSI demonstrated 2 times higher temporal SNR and 2 times larger activation region.
Introduction
Oscillating Steady-State Imaging (OSSI)1 establishes a newly described steady state by combining balanced gradients and quadratic RF phase progression with large phase increments. This steady-state signal combines the high SNR feature of the balanced steady state and the T2’ contrast of GRE imaging. However, due to the periodic oscillation of OSSI signals, the temporal resolution of OSSI fMRI can be compromised by the need to acquire and combine images across the period of oscillation, and the spatial resolution is limited by the short TR.Past works on improving spatio-temporal resolution for fMRI used matrix low-rank2 or low-rank plus sparse models3. We found them insufficient for OSSI because OSSI oscillations are neither low-rank nor sparse along time. Therefore, we structure OSSI images to have two time dimensions and apply a patch-tensor low-rank model to simultaneously exploit redundancy in the oscillatory pattern of OSSI and repetition along the fMRI time course.
Together with a prospective undersampling scheme, we can reconstruct high-resolution 3D OSSI images with less than 10% of the fully sampled k-space data. Compared to Ernst angle GRE imaging with TE = 30 ms, the proposed OSSI acquisition and reconstruction led to a factor of 2.2 improvement in both the number of activated voxels and average tSNR within the brain.
Methods
4D OSSI images ($$$x \times y \times z \times t$$$) are reshaped to 5D ($$$\mathbf{X}\in\mathbb{C}^{x \times y \times z \times n_c \times t_s}$$$) for the tensor model reconstruction. $$$n_c$$$ is the fast oscillation time dimension ("fast time"), and $$$t_s$$$ is the fMRI time dimension ("slow time"). Because the 3D patch tensors ($$$xyz \times n_c \times t_s$$$) of the 5D data are low-rank and can be unfolded to 3 spatial-temporal low-rank matrices, we build the cost function with consensus ADMM4 as$$\underset{\mathbf{Z}_i,\mathbf{X}}{\operatorname{minimize}}\ \sum_{\mathcal{P}} \sum_{i = 1}^{3}\lambda_i\lVert\mathcal{P}\big(\mathbf{Z}_i\big)_{(i)}\rVert_* + \frac{1}{2}\lVert\mathcal{A}\big(\mathbf{X}\big)-\mathbf{b}\rVert_2^2\\
\mbox{subject to}\ \ \mathbf{Z}_i - \mathbf{X} = 0,\ i = 1,...,3.$$ Here $$$\mathcal{P}(\mathbf{\cdot})$$$ form the 3D low-rank patch tensors, $$$\mathcal{P}(\mathbf{Z})_{(i)}$$$ denotes mode-$$$i$$$ unfolding of the patch tensor, $$$\lambda_i$$$s are regularization parameters, $$$\mathcal{A}(\mathbf{\cdot})$$$ is a linear operator consists of coil sensitivities, NUFFT and sparse sampling, and $$$\mathbf{b}$$$ represents k-space measurements. With the augmented Lagrangian of the cost function, we sequentially update the variables for a number of iterations to determine the reconstructed images $$$\mathbf{X}$$$.
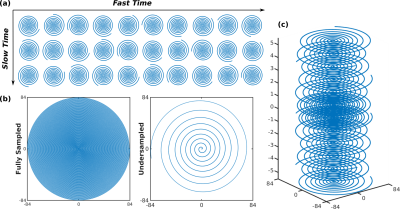
For prospective undersampling, we designed a variable-density spiral based on5 with uniform sampling density in the k-space center and a linearly decreasing sampling density to the edge of k-space. Each frame was acquired with one spiral, and pseudo-randomized Golden-angle rotations were applied between frames to increase sampling incoherence along each of the two dimensions as shown in Figure 2 (a). For 3D undersampling, we implemented a stack of the variable-density spirals with increased in-plane sampling at the center of $$$k_z$$$ and Golden-angle rotation between $$$k_z$$$ planes as in Figure 2 (c).
All the data were collected on a 3T GE MR750 scanner with a 32-channel Nova Medical head coil. OSSI was compared to GRE with matched spatial resolution of $$$1.3 \times 1.3 \times 2.5$$$ mm$$$^3$$$, and temporal resolution of $$$150$$$ ms for 2D and $$$2.1$$$ s for 3D. For OSS, we set TR = 15 ms, $$$n_c$$$ = 10 images per oscillation, spiral-in TE = 11.2 ms, flip angle = 10$$$^\circ$$$, and number of $$$k_z$$$ planes = 12 for 3D. For GRE, multi-shot acquisition with number of interleaves = 3, TR = 50 ms for 2D, multi-slice TR = 700 ms with 14 slices, spiral-in TE = 30 ms, and Ernst flip angle = 16$$$^\circ$$$ was used. The GRE images were reconstructed with conjugate gradient (cg)-SENSE6,7 and an edge-preserving regularizer.
The human fMRI task with was a left vs. right reversing-checkerboard visual stimulus of 210 s with 10 s rest, 5 cycles of left or right stimulus of 20 s (20 s L/20 s R $$$\times$$$ 5 cycles). The OSSI fMRI images were generated by 2-norm combination of the fast time dimension.
Results
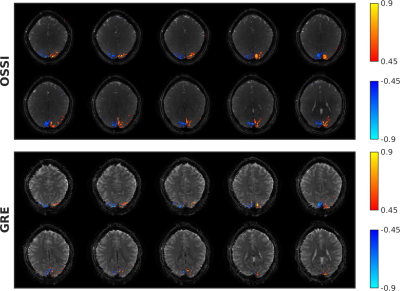
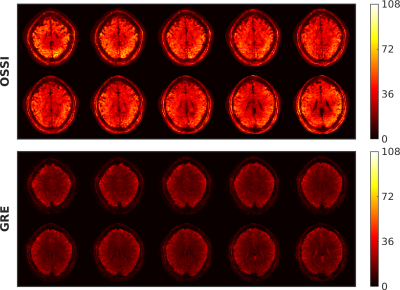
Figure 2 presents the proposed prospective undersampling pattern with a factor of 12 acceleration for 2D imaging and a factor of 10 acceleration for 3D imaging. For 2D, OSSI tensor reconstruction recovers the high-resolution structures and well preserves the functional activations compared to regularized cg-SENSE reconstruction, and shows 4 times more activations and 3 times larger average tSNR compared to Ernst angle GRE with the same spatial-temporal resolution (Figure 3). High-resolution 3D OSSI with tensor model reconstruction outperforms multi-slice GRE by a factor of 2.2 in terms of the amount of functional activity (Figure 4) and average tSNR within the brain (Figure 5).Conclusion
OSSI tensor model for prospectively undersampled 2D and 3D reconstructions demonstrated high-resolution fMRI images with 2 times improved tSNR and activations in comparison to Ernst angle GRE imaging.Acknowledgements
We wish to acknowledge the support of NIH Grants R01EB023618 and U01EB026977.References
1. Shouchang Guo and Douglas C. Noll, ''High SNR Functional MRI Using Oscillating Steady State Imaging". Joint Annual Meeting ISMRM-ESMRMB, Paris 2018, In Proc. Intl. Soc. Mag. Reson. Med.
2. Chiew, Mark, et al. "k‐t FASTER: acceleration of functional MRI data acquisition using low rank constraints." Magnetic resonance in medicine 74.2 (2015): 353-364.
3. Petrov, Andrii Y., Michael Herbst, and V. Andrew Stenger. "Improving temporal resolution in fMRI using a 3D spiral acquisition and low rank plus sparse (L+ S) reconstruction." NeuroImage 157 (2017): 660-674.
4. Boyd, Stephen, et al. "Distributed optimization and statistical learning via the alternating direction method of multipliers." Foundations and Trends® in Machine learning 3.1 (2011): 1-122.
5. Lee, Jin Hyung, et al. "Fast 3D imaging using variable‐density spiral trajectories with applications to limb perfusion." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 50.6 (2003): 1276-1285.
6. Pruessmann, Klaas P., et al. "Advances in sensitivity encoding with arbitrary k‐space trajectories." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 46.4 (2001): 638-651.
7. Sutton, Bradley P., Douglas C. Noll, and Jeffrey A. Fessler. "Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities." IEEE transactions on medical imaging 22.2 (2003): 178-188.
Figures