3794

Quantitative T2 Mapping using Accelerated 3D Stack-of-Spiral GRE Acquisition

Ruoxun Zi¹, Dan Zhu^1,2, Wenbo Li^2,3, and Qin Qin^2,3
¹Department of Biomedical Engineering, Johns Hopkins University School of Medicine, Baltimore, MD, United States, ²Russell H. Morgan Department of Radiology and Radiological Science, Johns Hopkins University School of Medicine, Baltimore, MD, United States, ³F.M. Kirby Research Center for Functional Brain Imaging, Kennedy Krieger Institute, Baltimore, MD, United States

Synopsis

We presented a T2 prepared stack-of-spiral gradient echo (GRE) pulse sequence with or without CSF nulling for T2 mapping of brain. T2 maps were iteratively optimized by data consistency, model consistency and spatial sparsity regularization using projected-gradients approach, which was evaluated by in vivo experiments and compared with SENSE, CS SENSE and model-based methods. The proposed reconstruction method provided better performance with normalized root mean square error (nRMSE) of the whole brain T2 estimation equal to 8.2±0.5% with an acceleration factor of 5. The T2 estimation with and without CSF nulling were consistent.

Introduction

Conventional T2 mapping procedure consists of acquisition of the same k-space datasets at different echo times, followed by individual image reconstruction and subsequent voxel-by-voxel model fitting. The long scan time associated with reliable parametric dimension sampling is an obstacle for practical utility and requires high undersampling at levels which are beyond capabilities of conventional reconstruction techniques such as parallel imaging^1,2. A variety of constrained reconstruction methods that utilize specific spatial, temporal or parametric characteristics have been developed.^3-5 A promising strategy is to utilize k-space data and signal decay model jointly to estimate parameter map directly from k-space data.^6-8 Most methods were implemented on Cartesian trajectory.^6-9 A few recent studies applied 3D radial trajectory for T1 and/or T2 estimation with higher efficiency.^10,11 Spiral trajectory¹² has been explored with advantages on insensitivity to motion artifacts and high acquisition efficiency, which indicates its potential on high acceleration.

In this work, we proposed a T2 prepared stack-of-spiral gradient-echo (GRE) pulse sequence with or without CSF nulling for 3D T2 mapping of brain and applied a model-based reconstruction method with spatial sparsity regularization for T2 estimation.

Methods

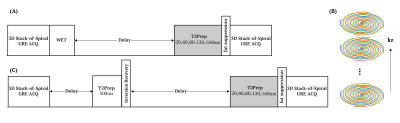
The pulse sequence diagram for T2 mapping is shown in Figure 1A. T2 preparation with 20, 40 ,80, 120, 160ms echo time were successively applied 1.50s after the WET pre-saturation pulse to generate different T2 contrast. 3D stack-of-spiral turbo-field-echo (TFE) acquisition was adopted, in which TFE encoding was applied along kz dimension (Figure 1B). The interleaves were rotated after every four shot-intervals. For the purpose of CSF nulling, a T2 prep (300ms) module and inversion pulse (1100ms) was implemented (Figure 1C), which saturates tissues with relatively short T2 values and thus rendering higher longitudinal magnetization after recovery¹³.

IIn vivo brain data were acquired on four healthy volunteers (3 females, age 44-59 yo). Three experiments were performed on each volunteer, which consisted (1) fully sampled equal-spaced spiral trajectory without CSF nulling, used as the reference of T2 estimation; (2) variable density spiral acquisition (Accel=2) without CSF nulling, and (3) variable density spiral acquisition (Accel=2) with CSF nulling. Each dataset was acquired with 1.2mm isotropic resolution, FOV =220$$$\times$$$220$$$\times$$$80mm³, TFE factor = 25. The total acquisition time was 11:00, 5:35 and 8:05 minutes separately.

The k-space dataset with variable density trajectory was retrospectively undersampled by selecting different interleaves to simulate an interleave-rotated and an interleave-no-rotated undersampled acquisition along parametric dimension with in-plane acceleration factor of 5.

For T2 estimation, a model-based iterative reconstruction method with spatial sparsity regularization was applied, which can be formulated as:
$$minimize \|S(\widetilde{S}(\bar{f}))-\bar{f}\|_1 + \alpha TV(\bar{f}) \qquad s.t. \|E(\bar{f})-y\|_2 < \epsilon$$
Where $$$\bar{f}$$$ is the parametric image series, $$$S$$$ is the T2 decay model, $$$\widetilde{S}$$$ is the inverse operator mapping from image series to T2 map, $$$E$$$ is the encoding matrix, $$$TV$$$ is the total variation operator, and $$$y$$$ is the measured k-space data. Parameter $$$\alpha$$$ trades sparsity with model consistency, and $$$\epsilon$$$ is chosen by the noise level. The algorithm was implemented using projected-gradient approach, which is similar to PG-MOCCO⁸. We iteratively optimized data consistency, model consistency and spatial sparsity regularization of images. For comparison purpose, we reconstructed images from the undersampled data of each T2 preparation separately using SENSE and CS SENSE, followed by voxel-wise fit, which did not utilize the correlation of k-space data in the parametric dimension, and also conducted direct T2 estimation using model-based method without spatial sparsity regularization.

Results and Discussion

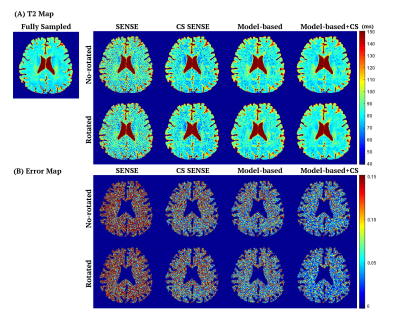
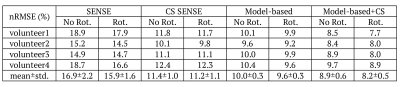
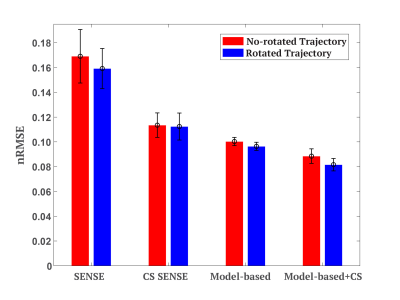
Figure 2 compares the T2 maps estimated by different reconstruction methods, which demonstrates that the proposed method provided lower noise level and better artifact reduction. The normalized root mean square error (nRMSE) measuring over 3D whole brain of each volunteer provided in Table 1 further proves that the proposed method yielded the highest accuracy, with nRMSE equal to 8.2$$$\pm$$$0.5% for acceleration factor of 5.

Figure 3 demonstrates that the k-space data in parametric dimension provided more information and potential on higher acceleration due to the smaller nRMSE of model-based methods, and that the spatial sparsity constraint further improved the accuracy of T2 estimation. Note that for each reconstruction method, the rotated undersampling scheme achieved better accuracy than the no-rotated one, which was more pronounced and stable in the model-based methods. This observation may be explained by the reason that different undersampling trajectory induces different artifacts which may be compensated and reduced when considering the k-space data along the parametric dimension jointly.

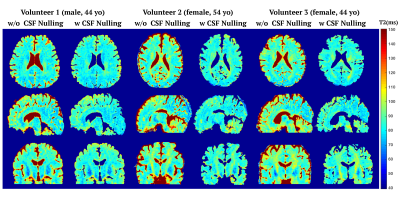
Figure 4 shows the cross-section T2 maps of three healthy volunteers estimated by the proposed method using the pulse sequence with and without CSF nulling. In the CSF nulling results, a mask was created based on the intensities of images with T2prep duration equal to 20ms, in which CSF have much lower intensity than other tissue. The nRMSE of T2 estimation with CSF nulling was 8.2$$$\pm$$$0.8%, which was in agreement with the performance without CSF nulling.

Conclusion

We presented a T2 prepared stack-of-spiral GRE pulse sequence with or without CSF nulling for 3D T2 mapping with whole-brain coverage. The iterative reconstruction method, which utilized the model consistency, data consistency and spatial sparsity jointly, provided reasonable T2 estimation with an acceleration factor of 5.

Acknowledgements

No acknowledgement found.

References

[1] Pruessmann, K. P., Weiger, M., Scheidegger, M. B., & Boesiger, P. (1999). SENSE: sensitivity encoding for fast MRI. Magnetic resonance in medicine, 42(5), 952-962.

[2] Lustig, M., & Pauly, J. M. (2010). SPIRiT: iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magnetic resonance in medicine, 64(2), 457-471.

[3] Lustig, M., Donoho, D., & Pauly, J. M. (2007). Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic resonance in medicine, 58(6), 1182-1195.

[4] Block, K. T., Uecker, M., & Frahm, J. (2007). Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magnetic resonance in medicine, 57(6), 1086-1098.

[5] Feng, L., Grimm, R., Block, K. T., Chandarana, H., Kim, S., Xu, J., ... & Otazo, R. (2014). Golden‐angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden‐angle radial sampling for fast and flexible dynamic volumetric MRI. Magnetic resonance in medicine, 72(3), 707-717.

[6] Sumpf, T. J., Petrovic, A., Uecker, M., Knoll, F., & Frahm, J. (2014). Fast T2 mapping with improved accuracy using undersampled spin-echo MRI and model-based reconstructions with a generating function. IEEE transactions on medical imaging, 33(12), 2213-2222.

[7] Sumpf, T. J., Uecker, M., Boretius, S., & Frahm, J. (2011). Model‐based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin‐echo MRI. Journal of Magnetic Resonance Imaging, 34(2), 420-428.

[8] Samsonov, A. (2015). Accelerated MR Parameter Mapping Using Robust Model-Consistency Reconstruction. Paper presented at the Meeting of the International Society for Magnetic Resonance in Medicine, Toronto, Ontario, Canada.

[9] Hilbert, T., Sumpf, T. J., Weiland, E., Frahm, J., Thiran, J. P., Meuli, R., ... & Krueger, G. (2018). Accelerated T2 mapping combining parallel MRI and model‐based reconstruction: GRAPPATINI. Journal of Magnetic Resonance Imaging, 48(2), 359-368.

[10] Keerthivasan, M. B., Saranathan, M., Johnson, K., Fu, Z., Weinkauf, C. C., Martin, D. R., ... & Altbach, M. I. (2019). An efficient 3D stack‐of‐stars turbo spin echo pulse sequence for simultaneous T2‐weighted imaging and T2 mapping. Magnetic resonance in medicine, 82(1), 326-341.

[11] Qi, H., Sun, J., Qiao, H., Zhao, X., Guo, R., Balu, N., ... & Chen, H. (2018). Simultaneous T1 and T2 mapping of the carotid plaque (SIMPLE) with T2 and inversion recovery prepared 3D radial imaging. Magnetic resonance in medicine, 80(6), 2598-2608.

[12] Pipe, J. G., & Zwart, N. R. (2014). Spiral trajectory design: A flexible numerical algorithm and base analytical equations. Magnetic resonance in medicine, 71(1), 278-285.

[13] Wong, E. C., Liu, T. T., Luh, W. M., Frank, L. R., & Buxton, R. B. (2001). T1 and T2 selective method for improved SNR in CSF‐attenuated imaging: T2‐FLAIR. Magnetic resonance in medicine, 45(3), 529-532.

Figures

Figure 1. (A) Schematic diagram of T2 prepared 3D stack-of-spiral sequence. The duration of T2 preparation was set as 20,40,80,120,160ms. (B) 3D stack-of-spiral trajectory, with TFE encoding applied on kz dimension and variable density spiral trajectory (Accel=2) applied in plane. (C) the pulse sequence with CSF nulling to remove the CSF partial volume effect.

Figure 2. (A) T2 maps and (B) corresponding normalized error maps estimated by different reconstruction methods (SENSE, CS SENSE, model-based method and model-based method with spatial sparsity regularization) and different undersampling schemes along parametric dimension (no-rotated and rotated trajectory). Reference value of T2 map was calculated based on the fully sampled data and voxel-wise fit.

Table 1. The normalized root mean squared error (nRMSE) of the T2 estimation by different reconstruction methods and undersampling schemes to the reference T2 map, measuring over the 3D whole brain of four volunteers.

Figure 3. Statistical comparison between different reconstruction methods and undersampling schemes in terms of nRMSE of T2 estimation measuring over the 3D whole brain of four volunteers.

Figure 4. Cross-section T2 maps of brains of three healthy volunteers estimated with and without CSF nulling. In CSF nulling case, a mask was created based on the intensities of CSF-nulling images for better visualization and identification of lesion without CSF partial volume effect.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3794