Introduction

The longitudinal relaxation rate, R1, is a useful proxy for myelination levels in the brain. The efficient variable flip angle (VFA) approach allows whole-brain estimation of R1 with high resolution in reasonable scan times¹. However, this method can be biased if motion occurs between the acquisition of data with different nominal flip angle due to position-specific modulation by the receiver coil profile². This violates the intrinsic model assumption that signal changes are due only to a change in flip angle. A simple correction method has been proposed² and shown to reduce bias to the level of scan-rescan reproducibility. However, it relies upon the acquisition of reference data from a coil with a relatively ‘flat’ sensitivity profile such as a body coil, which is generally not available at ultra-high field strength where localised transmit-receive coils are preferred.

To address this, we propose a framework that does not require body coil images. It considers the coil sensitivities as mapping a common signal between different intensity spaces. The framework ensures that the common signal is a Fréchet mean of the individual coil spaces with respect to a distance that penalises non-smooth mappings³. This allows the smooth sensitivity profile to be estimated directly from magnitude coil-wise images such that the resulting modulation can be removed. We demonstrate the ability of this novel approach to correct biases in R1 induced by inter-scan motion. This is done at 3T, where we can also compare performance against ² and at 7T where such a comparison is not possible due to the lack of a body coil or similar reference.

Methods

The magnitude image of each coil element is written as the product of the underlying flat signal and a smooth sensitivity field, up to additive (Gaussian) thermal noise. The log of these sensitivities is assumed to stem from a multivariate Gaussian distribution penalising their bending energy. These assumptions allow the joint log-likelihood of the mean signal and log-sensitivities to be defined and optimised:
$$\mathbf{r}^\star,\left\{\mathbf{z}_c^\star\right\}_{c=1}^C = \arg\max \sum_{c=1}^C \sum_{n=1}^N \frac{-1}{2\sigma_c^2} \left(b_{cn} r_n - x_{cn}\right)^2 + \sum_{c=1}^C \frac{-\lambda_c}{2} \mathbf{z}_c^{\mathrm{T}} \mathbf{L}\mathbf{z}_c + \mathrm{constant},$$
where $$$\left\{\mathbf{x}_c \in \mathbb{R}^N\right\}_{c=1}^C$$$ are $$$C$$$ magnitude images with $$$N$$$ voxels, $$$\mathbf{r} \in \mathbb{R}^N$$$ is the true signal, $$$\left\{\mathbf{b}_c\in\mathbb{R}^N\right\}_{c=1}^C$$$ are $$$C$$$ coil sensitivities and $$$\left\{\mathbf{z}_c = \ln\mathbf{b}_c \in\mathbb{R}^N\right\}_{c=1}^C$$$ are their logs. The thermal noise has variance $$$\left\{\sigma_c^2\right\}_{c=1}^C$$$, while the prior distribution has precision matrix $$$\lambda_c\mathbf{L}$$$, where $$$\mathbf{L} \in \mathbb{R}^{N\times N}$$$ encodes the bending energy⁴ and $$$\lambda_c$$$ is a coil specific regularisation factor. For an array coil, all $$$\lambda_c$$$ take the same value. However, if body coil images are available, they can be considered additional coils but with a larger regularisation parameter to account for their flatter profile. In this work, the noise variance was estimated from the data and $$$\lambda_c$$$ was set to 10⁵ mm⁴ for array coils and 10⁸ mm⁴ for body coils.

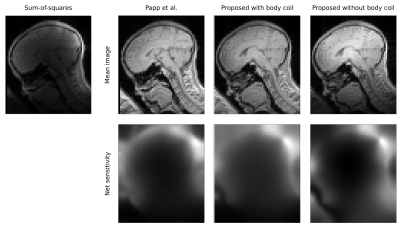
This problem is solved iteratively by updating, in turn, the mean image and the individual sensitivities as described in ³. Furthermore, at each iteration, the log-sensitivities are zero-centred and the mean image is scaled accordingly. This operation optimises the joint log-likelihood with respect to a scaling field $$$\mathbf{s} \in \mathbb{R}^N$$$ that acts on the mean space ($$$r=rs$$$, $$$b_c=b_c/s$$$). Finally, the net receive field of the array is the root sum-of-squares of the individual sensitivities: $$$b_r = \sqrt{\sum_{c=1}^C b_c^2}$$$. Since this net modulation is estimated on a per volume basis, it can accommodate changes due to inter-scan motion.

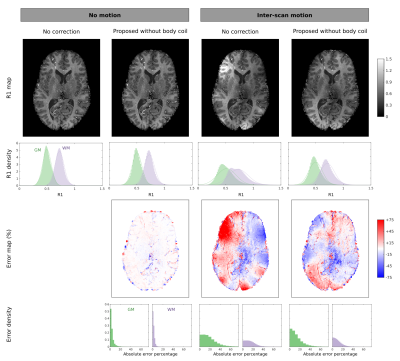
To validate our method, two datasets were acquired at 3T (64 channel coil) and 7T (32 channel coil): one PDw and two T1w volumes were acquired; participants were asked to move between the two T1w volumes, such that one of them is in alignment with the PDw volume while the other is not. Additionally, before each volume, a calibration scan was acquired with the array (3T, 7T) and body (3T) coils.

Sensitivity maps were estimated in three different ways at 3T: using the method of ², as implemented in the hMRI toobox⁵, and using our method, with (3T) or without (3T, 7T) including body coil images (Figure 1). In each case, R1 maps were estimated using the hMRI toolbox. Relative errors were computed with respect to the baseline maps from the no motion, no correction condition.

Results

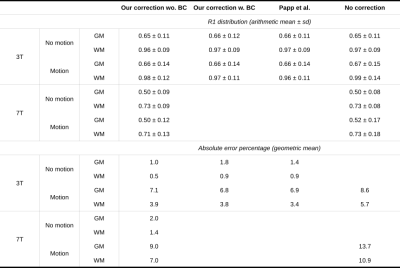
At 3T, our method with or without the body coil performed as well as ²: no major artefacts were introduced when no motion occurred, and most artefacts were corrected when inter-scan motion occurred (Figure 2).

At 7T, no major artefacts were introduced when no motion occurred, and most artefacts were corrected when inter-scan motion occurred (Figure 3).

Quantitative results are reported in Table 2.

Discussion & Conclusion

We proposed and validated a method for estimating the net sensitivity of an array coil, without needing a body coil. We showed at 3T that this method corrects inter-scan motion artefacts in R1 maps as well as methods using a body coil. Furthermore, we showed that this method can be used at 7T to greatly reduce inter-scan motion artefacts. At 7T, some bias remains, suggesting that the estimated mean space image is not perfectly flat. Improvement may be gained by regularising the mean image to favour flat intensities.