3762

Tissue based denoising for MR fingerprinting via long short-term memory networks

Gastao Cruz¹, Thomas Kuestner¹, Ilkay Oksuz¹, Olivier Jaubert¹, Niccolo Fuin¹, Andy P. King¹, Julia A. Schnabel¹, René M. Botnar¹, and Claudia Prieto¹
¹Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom

Synopsis

Conventional Magnetic Resonance Fingerprinting (MRF) relies on pixelwise dictionary matching of highly undersampled time-series images. However, remaining aliasing artefacts in these images can compromise the matching step and thus affect the accuracy of the parametric maps. Dictionary-based compression has been proposed to exploit redundancies in the signal evolution dimension, however these approaches do not exploit tissue redundancies within the images. Here we propose to leverage redundant information between similar tissues and the MRF dictionary to suppress residual artefacts along time, using long short-term memory (LSTM) networks. Preliminary results indicate that proposed MRF-LSTMs can suppress aliasing in highly undersampled scenarios.

INTRODUCTION:

Magnetic Resonance Fingerprinting (MRF¹) samples the magnetization transient state via highly undersampled images to produce multi-parametric maps (e.g. T1, T2, T2*). Despite some resistance to incoherent artefacts, aliasing can propagate from the undersampled images to the resulting maps^2,3. Iterative reconstruction approaches have been proposed to estimate images free of artefacts. In particular, locally low rank (LLR)^4,5and dictionary-based regularization³ have been proposed to exploit redundancies in the MRF signal evolution and have shown to suppress residual noise-like artefacts. Fully connected networks and recurrent neural network that exploit the time-dependent information of the MRF signal evolution (fingerprint) have been proposed to learn the maps without direct dictionary matching^6,7. Spatial-temporal convolutional neural networks have been proposed to take advantage of the information between neighbouring fingerprints⁸. However, these approaches may not necessarily exploit non-local tissue redundant information within the field of view. Here we train a neural network of long short-term memory (LSTM)⁹ units, leveraging both similar tissue-temporal signal evolutions and MRF dictionary prior information to reduce artefacts in resulting MRF maps. The proposed network was evaluated in realistic brain simulations and compared against low-rank inversion (LRI) reconstruction and LLR denoising.

METHODS:

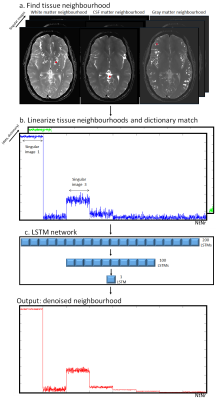
The proposed framework for MRF denoising is outlined in Fig.1, which acts in dictionary-based temporally compressed singular images³ (resulting from an LRI reconstruction) of size [Ny, Nx, Nr], where Ny and Nx are the image spatial dimensions and Nr is the number of singular images. Data is processed for each pixel separately, according to the following steps. 1) For each pixel in the singular images, a non-local neighbourhood of Nt self-similar tissues is obtained via exhaustive inner product with every other voxel (Fig.1a). 2) Each neighbourhood (containing multiple pixels over several singular images) forming the input signal of the MRF-LSTM network is stored in the first dimension (blue signal) of a NtNrx2 singular-neighbourhood matrix representing the singular pixels for this tissue neighbourhood. The corresponding signal matches (green signal) with the MRF dictionary are obtained (also via inner-product) and stored in the second dimension (Fig1.b). 3) This information is fed into the proposed MRF-LSTM network consisting of LSTMs with 3 layers: 200 LSTM units, 100 LSTM units and 1 LSTM unit, producing a denoised tissue group (Fig.1c). This procedure is independently performed for every pixel in the image and finally results are re-aggregated into the shape of the singular images.

EXPERIMENTS:

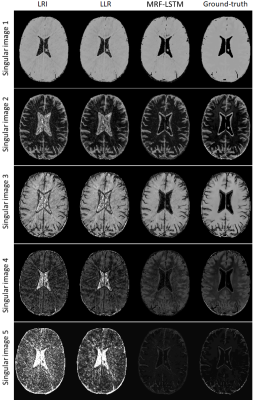
Brain T1, T2 and M0 maps obtained in previous in-vivo experiments in five healthy subjects were used as ground-truths for the simulation experiments. An acquisition was simulated based on pseudo-steady state MRF¹⁰ with the following key parameters: initial inversion recovery pulse, balanced steady state readout, TE/TR = 2/4.4 ms, 1x1 mm² resolution, varying flip angle according to¹⁰ and golden radial trajectory with one readout per time-point. The tissue neighbourhood Nt was 200 and the LRI rank Nr was 8. The simulation was performed with varying signal-to-noise ratio (SNR) levels ([20, 10, 5]) and varying number of time-points ([1000, 2000]). Singular images were reconstructed from this simulated data via LRI, which still contained residual streaking and blurring artefacts from radial undersampling. LRI reconstructed singular images formed the input for both the MRF-LSTM denoising and LLR denoising. The proposed MRF-LSTM framework was applied to the magnitude of reconstructed singular images and compared with LLR reconstruction (which used the complex signal). Ground-truth singular images (labels) were generated via the same simulation framework, based on fully sampled images. The MRF-LSTM network was trained with data from four healthy subjects resulting in approximately 1 million singular-neighbourhood training samples, 30 epochs, 0.01 learning rate, ADAM¹¹ optimizer, mean square error loss, 10% validation data. A fifth healthy subject dataset was used for testing. Resulting T1/T2 maps were obtained via inner-product with the MRF dictionary in all cases.

RESULTS:

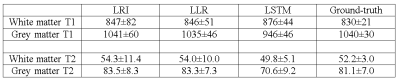
The proposed MRF-LSTM network was able to suppress undersampling artefacts in the singular value images to a higher degree than LLR, which is more visible in singular images with higher rank (Fig.2). When inspecting the resulting parametric maps the MRF-LSTM also achieved higher aliasing suppression than LLR and LRI (Fig.3). However, in these preliminary results the MRF-LSTM network failed to distinguish between white and grey matter, introducing a negative bias for grey matter in the parametric maps, possibly due large tissue grouping or excessive artefacts in the training samples. This bias can be seen in the T1 and T2 values obtained in regions of interest for white matter and grey matter in Table 1.

CONCLUSION:

An MRF-LSTM network was proposed for denoising of highly-undersampled MRF images, combining information from similar tissues and MRF dictionary prior information. Preliminary results suggest this approach could act as a powerful denoiser, however further network training is needed to better distinguish between white and grey matter in the parametric maps. Future work will improve the existing network and incorporate an improved network into a model based deep learning reconstruction to enforce data consistency within a LRI-based reconstruction.

Acknowledgements

ACKNOWLEGDMENTS: This work was supported by EPSRC (EP/P001009, EP/P032311/1) and Wellcome EPSRC Centre for Medical Engineering (NS/ A000049/1).

References

1. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature 2013;495:187–192.

2. Doneva M, Amthor T, Koken P, Sommer K, Börnert P. Matrix completion-based reconstruction for undersampled magnetic resonance fingerprinting data. Magn. Reson. Imaging 2017;41:41–52 doi: 10.1016/j.mri.2017.02.007.

3. Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn. Reson. Med. 2018;79:83–96 doi: 10.1002/mrm.26639.

4. Lima da Cruz G, Bustin A, Jaubert O, Schneider T, Botnar RM, Prieto C. Sparsity and locally low rank regularization for MR fingerprinting. Magn. Reson. Med. 2019;81:3530–3543 doi: 10.1002/mrm.27665.

5. Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, Lustig M. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med 2017;77(1):180-95.

6. Cohen O, Zhu B, Rosen MS. MR fingerprinting deep reconstruction network (DRONE). Magnetic resonance in medicine. 2018 Sep;80(3):885-94.

7. Oksuz I, Cruz G, Clough J, Bustin A, Fuin N, Botnar RM, Prieto C, King AP, Schnabel JA. Magnetic resonance fingerprinting using recurrent neural networks. In2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) 2019 Apr 8 (pp. 1537-1540). IEEE.

8. Hoppe E, Körzdörfer G, Würfl T, Wetzl J, Lugauer F, Pfeuffer J, Maier AK. Deep Learning for Magnetic Resonance Fingerprinting: A New Approach for Predicting Quantitative Parameter Values from Time Series. InGMDS 2017 Sep 26 (pp. 202-206).

9. Hochreiter S, Schmidhuber J. Long short-term memory. Neural computation. 1997 Nov 15;9(8):1735-80.

10. Assländer J, Glaser SJ, Hennig J. Pseudo steady-state free precession for MR-fingerprinting. Magnetic resonance in medicine. 2017 Mar;77(3):1151-61.

11. Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. 2014 Dec 22.

Figures

Figure 1. Framework of the proposed approach for MRF image denoising via long short-term memory networks (LSTM), applied for each tissue: a) identify a neighbourhood of similar tissues (via exhaustive inner product with every other voxel), b) perform dictionary match and reshape both the data tissue group and the dictionary tissue group, c) denoise this tissue-grouped fingerprint by an LSTM network with 3 layers: 200 LSTMs, 100 LTMs, 1 LSTM to produce a denoised tissue neighbourhood.

Figure 2. Reconstructed singular images (ranks one through five) for the Low Rank Inversion (LRI) which are denoised by locally low rank (LLR) denoising applied to LRI and MRF long short-term memory (LSTM) network in comparison the ground-truth. Artefacts present in the LRI images are reduced with LLR and further reduced with MRF-LSTM, however some artefacts remain in comparison to the ground-truth.

Figure 3. T1 and T2 maps for the Low Rank Inversion (LRI), locally low rank (LLR) denoising applied to LRI, MRF long short-term memory (LSTM) network applied to LRI and the ground-truth. Considerable artefacts (streaking and blurring from radial undersampling) are visible in the LRI maps and are reduced with LLR. These artefacts are further reduced with the LSTM network, however an underestimation bias is introduced in the grey matter.

Table 1: Mean and standard deviation of T1 and T2 values in regions of interest for different tissues (in ms).

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3762