Purpose

Magnetic resonance fingerprinting (MRF) [1] is a novel and effective approach for MR parametric quantification. 3D MRF technique was then developed for further acceleration and larger slice coverage. The artifact correction and pattern recognition of such additionally undersampled data are based on either the sparsity in a temporal-frequency domain [2] or variants of parallel imaging technique [3]. In this work, we proposed a new 3D MRF acquisition and reconstruction strategy using the framework of Alternating Direction Method of Multipliers (ADMM) to exploit both sparsity constraint and coil sensitivity. Our method permits the quantification of MR parameter (T₁, T₂) for a 3D volume with reduced scan time.

Methods

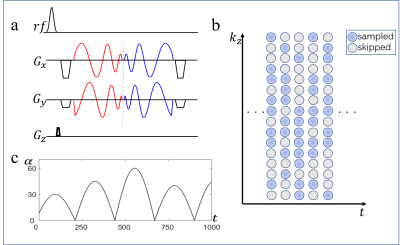
Acquisition: In this study, a 3D FISP-MRF [4] sequence was used with a stack-of-spiral acquisition, and spiral in-out trajectories were used as readout [5]. The sequence diagram of one TR is shown in Fig 1a. To further reduce the coherence of artifacts along slice direction, a pseudo-randomized kz-t sampling pattern was generated, whereby the k-space center was more densely sampled (e.g., in Fig 1b for an example of undersampling factor R = 2 along kz). Pseudorandomized flip angle train (Fig 1c), and constant TR and TE were used.
Reconstruction: ADMM has been used for 2D MRF reconstruction to improve the matching fidelity [6, 7]. In this work, a 3D extension of ADMM with low-rank approximation and sparsity constraints is proposed. The augmented Lagrangian is $$\ell_{\mu}(x,D,y) = ||Ex-m||_2^2+\mu||x-DD^Hx+y||_2^2+\mu_1||Wx||_1+\mu_2|x|_{TV}$$
where m represents the measured multi-channel k-space data, x the reconstructed image, E the encoding matrix comprising of 3D sampling, gridding, Fourier transform, coil sensitivity and low-rank approximation, D the dictionary projected to low-rank subspace, and the last two terms are regularization terms for wavelet and total variation. To achieve fast convergence, singular vector dependent $$$\mu_1$$$ and $$$\mu_2$$$ was used as weightings in the regularization term, i.e., $$$||Wx||_1$$$ during ADMM iterations such that convergence was achieved in 5 iterations.
Experiment: All MRI experiments were performed using a 3T MRI scanner (Achieva TX, Philips Healthcare) with an 8-channel head coil for the signal reception. A 3D FISP-MRF sequence was performed with the following imaging parameters: FOV = 300 x 300 x 32 mm3 for each slab, resolution = 1.17 x 1.17 x 2 mm3, TR = 12.5 ms, TE = 6 ms, spiral-in-spiral-out readout with acquisition window = 8.4ms and undersampling factor = 58.4, and 1000 TRs for each kz encoding. Delay time of 5 s was inserted between consecutive kz encoding. The scan time for each 3D MRF data was 275, 135 and 82.5 seconds for R = 1, 2 and 3 along kz, respectively.

Results and Discussions

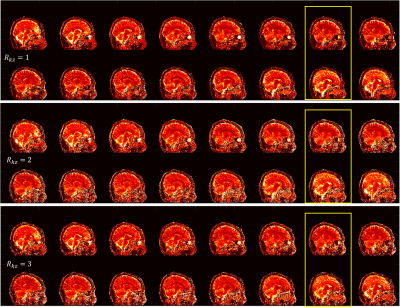
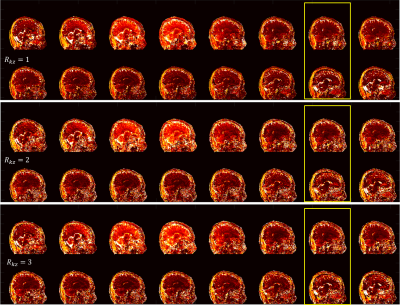
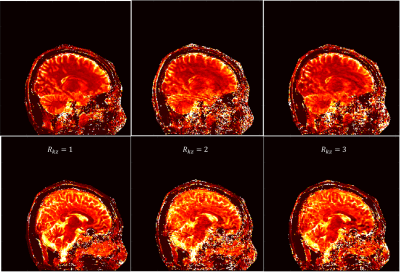
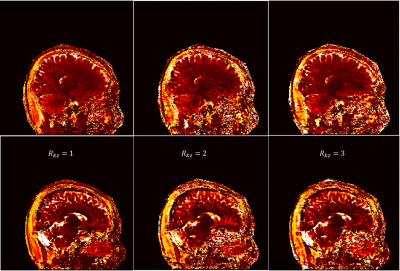
Fig 2 and Fig 3 show the sagittal T1 and T2 maps respectively with both undersamplings along kz (R_kz) of 2 and 3. Results from fully sampled kz (left column) are also shown as reference. The parameter maps from R_kz = 2 and R_kz = 3 obtained from our proposed method are comparable to those from fully sampled kz, suggesting that 3D MRF can be accelerated along kz. Usually when MRF is accelerated along kz, more dynamics per kz encoding would be required to ensure sufficient encoding capability. Nevertheless, with our proposed method, sparsity is additionally provided by the sampling pattern and fully used by regularized ADMM, so an increase in the number of dynamics is not required. Moreover, the use of spiral-in-spiral-out readout guaranteed better performance with such undersampling. In the 3D-ADMM algorithm, low-rank approximation was used to compress the data, and singular-value-weighted regularization was used as sparsity constraint for fast convergence, although the computational cost of the reconstruction warrants further improvement in future studies. The coil sensitivity constraint in this study was achieved by an 8-channel coil, so it would be conceivable that the result could be further improved and larger kz undersampling factor could be achieved by using more coil elements.

Conclusion

In this work, we demonstrated a new approach for 3D MRF acquisition and reconstruction using ADMM. With this strategy, comparable parametric maps can be acquired with reduced scan time. The effective scan time for R=3 and whole-brain MRF is less than 7 minutes.

Acknowledgements

No acknowledgement found.