Introduction

Magnetic Resonance Fingerprinting (MRF) has been successful used to simultaneously estimate T1 and T2 values using a balanced Steady State Free Precession (bSSFP) acquisition¹. It has been shown that MRF-bSSFP with spiral sampling can retain the spin history and achieves high signal to noise ratio (SNR) and scan efficiency². However, banding artefacts produced by off-resonance effects in the bSSFP sequence can affect the quality of the parametric maps³. Moreover, the spiral acquisition causes blurring due to off-resonance³. Ostenson et al.⁴ proposed a correction for unbalanced SSFP, however this approach only considers smooth variations of field maps. A general theoretical approach to correct for off-resonance distortions has been proposed for conventional (non-MRF) spiral MR imaging⁵. Here we propose to extend this approach to correct off-resonance effects in MRF-bSSFP acquisitions. The feasibility of the proposed approach was evaluated in a realistic brain simulation and standardized T1/T2 phantom acquisition.

Method

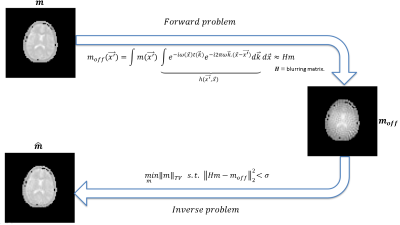
Off-resonance correction: to reduce the off-resonance artifacts we estimate the point spread function (PSF) for each TR simulating the sequence for a unitary pixel in all positions using the field map estimated by the conventional MRF. This allow us to build a blurring matrix H, such that:
$$m_{off} = Hm \quad \quad (Eq.1)$$
where $$$m_{off}$$$ is the corrupted data and $$$m$$$ is the desired corrected data. For an $$$N\times N$$$ image, the $$$H$$$ matrix size is of $$$N^{2}\times N^{2}$$$ and the columns of $$$H$$$ corresponding to the pixel at location $$$(p,q)$$$ is obtained by column ordering of $$$PSF(p,q) = FFT^{-1} \{e^{-j\omega (p,q)t(r,s)}\} $$$ shifted by $$$(p,q)$$$, where $$$\omega$$$ is the off-resonance frequency and $$$t$$$ is the acquisition time. To estimate a corrected image, for each TR, we solved the inverse problem using Total Variation (TV) deblurring (see Fig. 1):
$$ \min_{m} ||m||_{TV} \quad s.t \quad ||Hm -m_{off}||_{2}^{2} \quad \quad (Eq.2) $$
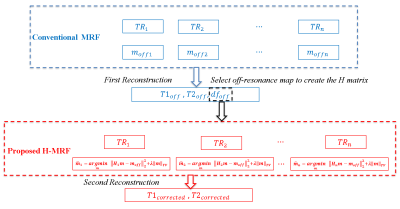
We used UNLocBoX⁷ (a convex optimization toolbox for MatLab) to solve the TV deblurring. Figure 2 shows a schematic summary of the comparison between the conventional MRF-bSSFP without off-resonance correction and the proposed matrix based on off-resonance correction approach (H-MRF).

Experiments: the proposed approach was tested in realistic brain simulations, and an acquisition on standardized T1/T2 phantom⁶ with two bottles of oil nearby to generate a distorted field map. The acquisition was performed on a 1.5 T scanner (Ingenia, Philips, Best, The Netherlands) using a 32‐element head coil. Relevant acquisition parameters included: Flip Angles (FA) between 0º-80º after an RF inversion pulse¹, 1000 random Repetition Times (TR) between 14.5-18.0 ms, balanced gradients in each TR, and a spiral readout of 18 interleaved with 5.58 ms of readout time.The echo time (TE) was 7.25 ms, and was constant for each TR. The FOV was 128$$$\times$$$128 mm (simulations) and 288$$$\times$$$288 mm (phantom acquisitions) with in-plane resolution of 2$$$\times$$$2 mm and 8 mm slice thickness.

Dictionary generation: the fingerprints were generated using the Bloch equation for a range of T1, T2 and df (off-resonance) values: T1(400 to 2000 ms, steps of 10 ms), T2 (40 to 300 ms, steps of 4 ms), and df (off-resonance, -250 to 250 Hz, steps of 2 Hz). Parametric values were obtained by matching the measured signal to the closest dictionary entry using the maximum dot product.

Analysis of results: T1 and T2 values estimated with conventional MRF-bSSFP and the proposed H-MRF approach are compared using normalized root mean square error (NRMSE).
.

Results and discussion

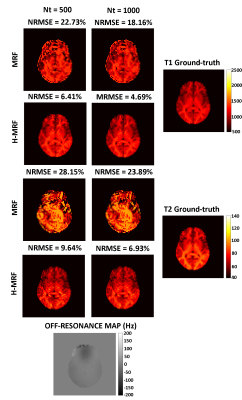
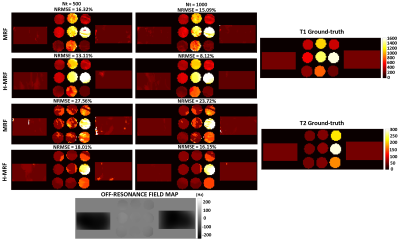
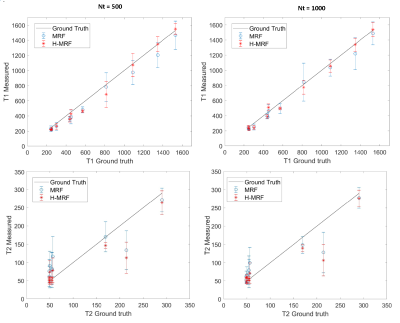
Reconstructed T1 and T2 maps using MRF and proposed H-MRF with different number of time points (Nt = 500 and Nt = 1000) are shown in Fig. 3 for the brain simulation. Strong artifacts are observed in both T1 and T2 maps with conventional MRF, whereas decreased artifacts are observed with the proposed H-MRF approach for both 500 and 1000 time points. NRMSE decreases for both methods with the number of time-points, however H-MRF achieved lower errors than conventional MRF. T2 NRMSEs at Nt = (500,1000) were (28.15%,23.89%) and (9.64%,6.93%) for MRF and H-MRF, respectively, whereas T1 NRMSEs at Nt = (500,1000) were (22.73%,18.16%) and (6.41%,4.69%) for MRF and H-MRF, respectively.

Reconstructed T1 and T2 maps using MRF and proposed H-MRF with 500 and 1000 time points are shown in Fig. 4 for phantom acquisition. T1 and T2 values estimated with conventional MRF and H-MRF are compared against ground truth in Figure 5. Phantom acquisition presents similar results with both 500 and 1000 time points. H-MRF achieves lower T2 NRMSEs ((18.01%,16.15%) at Nt = (500,1000)) than conventional MRF ((27.56%,23.72%) at Nt = (500,1000)). Similarly, T1 NRMSEs are lower with H-MRF (13.11%,8.12%) in comparison to conventional MRF (16.32%,15.09%) at Nt = (500,1000). Figure 5 shows that H-MRF has better accuracy than conventional MRF for T2 values lower than 100 ms (brain tissues). H-MRF shows higher T1 precision in comparison to conventional MRF.

Conclusion

A novel and general approach H-MRF has been proposed to correct for off-resonance distortions in bSSFP-MRF with spiral sampling effects from corrupted images. H-MRF improved the quality of reconstructions in comparison to conventional MRF, particularly in its precision for brain tissues. Future work will be performed to validate the proposed approach in-vivo acquisitions.