Introduction

Due to high cost and limited patient tolerance of MRI, our field is constantly searching for faster, more precise MRI exams. Acceleration in MRI is readily achieved with techniques such as undersampling and non-Cartesian sampling in k-space. One example is MR fingerprinting (MRF) [1], which often uses a spiral trajectory with high undersampling factor. Reconstruction is often performed using the nonuniform FFT (NUFFT) [2], including the additional steps of gridding and density compensation. As undersampling leads to dominating aliasing artifacts and can be a significant source of error, we want to determine how to optimally sample both in time and space. For the simplest implementation of MRF, this means optimizing the flip angle and TR as functions of time.

Sequence optimization in MRI and MRF [3]–[6] looks for optimal acquisition patterns with an application-specific cost function. Gaussian noise is often used to model both random noise and undersampling artifacts, however, it often does not accurately represent non-Cartesian undersampling artifacts. For these, direct simulation of the artifacts is most accurate, however, applying gridding and NUFFT in an iterative optimization is computationally expensive and impractical for rapid sequence optimization and evaluation. With hundreds to thousands of timepoints in MRF, the number of gridding and NUFFT computations increase to the point where the optimization process is dominated by NUFFT calculations.

We propose a partially separable model to estimate undersampling artifacts directly in the image domain. The spatial response of the non-Cartesian undersampling is precalculated from a limited number of segmented tissue masks and the time-varying signal intensity is simulated separately. The resulting time-resolved undersampled images are calculated directly as the product of the spatial response and signal intensity, eliminating the need for NUFFT inside the optimization iterations. This model can be precalculated using any segmented digital phantom, and can be applied to any iterative method in MR where undersampling artifacts need to be repeatedly simulated. We show an over 100x improvement in optimization speed using this method.

Methods

Assuming a limited number of tissue types in the brain, a series of fully sampled and time-resolved images can be modeled as $$$I_{full}(x,y,t) = \sum_{i=1}^J P_i(x,y) d_i(t),$$$ where J is the number of tissue types, $$$P_i(x,y)$$$ is the mask with the probability of each pixel belonging to tissue class i, and $$$d_i(t)$$$ is the signal intensity in time for tissue i. The undersampled images can be calculated as
$$I_{us}(x,y,t) = F_{us}^{-1} S F_{full} (I_{full}) = \sum_{i=1}^J F_{us}^{-1} S F_{full}(P_i(x,y))d_i(t)$$
where $$$F_{full}$$$ and $$$F_{us}$$$ are fully sampled and undersampled NUFFT and S is the undersampling pattern. In this model, the NUFFT operators are only applied on the spatially dependent tissue masks, which is independent from the particular spin evolution. Because we assume that the sampling pattern is determined a priori, the spatial response $$$P_{us_i} = F_{us}^{-1}S F_{full}(P_i(x,y))$$$ can be precalculated, while only $$$d_i(t)$$$ is updated during the optimization.

For MRF sequence optimization, we developed a numerical brain phantom segmented into three tissues: white matter, gray matter, and cerebrospinal fluid (CSF), shown in Figure 1. With the spiral sampling previously described [1], 48 highly undersampled images for each of the three masks, denoted $$$P_{us_{wm}}(x,y,S), P_{us_{gm}}(x,y,S)$$$ and $$$P_{us_{csf}}(x,y,S)$$$, were derived as functions of position $$$(x,y)$$$ and sampling pattern S. Examples of the undersampling artifacts for each of the three masks from two different spiral trajectories are in Figure 2.

Using an MRF sequence with 480 time points, three signal evolutions were simulated to correspond to each of WM, GM, and CSF, denoted $$$d_{wm}(t), d_{gm}(t)$$$, and $$$d_{csf}(t)$$$, respectively, using T1 and T2 values from the literature. Note that these signal evolutions are the same for all pixels within each tissue mask. To approximate undersampling at a pixel location $$$(x,y)$$$, the three simulated tissue signals are multiplied by the corresponding spatial response based on (1).

Results

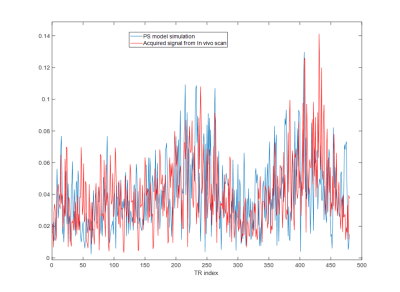
The reconstructed signals (with approximate and actual NUFFT gridding) from the phantom were matched to a dictionary. Errors in regions of WM, GM, and CSF were computed, shown in Figure 3. Percent errors in T1 and T2 were identical for both methods in each of the respective regions, showing that the partially separable method can accurately model errors from undersampling. Calculations using the proposed method were significantly faster. Reconstructing one slice of the digital phantom with one iteration of gridding and NUFFT took 151 seconds, compared to 1.1 seconds for the proposed partially separable method.

Figure 4 compares a signal evolution of the WM simulated from the brain phantom using the partially separable model to an acquired signal at a WM location from an actual in vivo scan. The scale of the aliasing artifacts from the simulation closely matches that from the in vivo measurement, validating our model for the approximation of aliasing artifacts from the actual scan.

Discussion

This model for producing signal evolutions with approximated undersampling artifacts is a computationally rapid method to evaluate the tolerance of a sequence to undersampling. The framework proposed here is not limited to MRF or brain applications, rather, it can be applied to any MR application where rapid estimation of undersampling artifacts is desired without using gridding and NUFFT. Iterative optimization of an MR sequence is one example.

Acknowledgements

The authors would like to acknowledge funding from Siemens Healthineers, Microsoft and NIH grant EB026764-01 and NS109439-01