3744
Quantum Optimization Framework for MR Fingerprinting Framework Incorporating Undersampling and Noise1Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, 21Qbit, Vancouver, BC, Canada, 3Radiology, Case Western Reserve University, Cleveland, OH, United States, 4Microsoft, Redmond, WA, United States
Synopsis
MR fingerprinting is a novel quantitative MR imaging technique that provides multiple tissue properties maps simultaneously. Designing appropriate MR fingerprinting sequence patterns is crucial to speed up data acquisition while obtaining accurate measurements. Here we propose an advanced MR fingerprinting optimization framework that incorporates undersampling artifacts and random noise in the cost function which directly compute quantitative errors in the result maps. We use quantum-inspired algorithm to solve the problem and generate optimized sequences. In both simulation and in vivo experiments, the optimized sequence showed improved image quality and measurement accuracy.
Introduction
MR Fingerprinting (MRF) is a quantitative imaging method that simultaneously provides multiple tissue property maps1. To achieve precise and accelerated scans, optimization of MRF sequence patterns has long been the goal of MRF research but has been challenging due to the large number of degrees of freedom in the MRF design. Most of the current methods are based on indirect measurements, such as dictionary orthogonality and signal magnitude, or assume that the signal is only affected by random noise without considering undersampling artifacts2,3. Here we propose an advanced MRF optimization framework that 1) implements a fast-computing model that accounts for measurement noise and aliasing artifacts from any arbitrary sampling trajectories, and 2) constructs a cost function that directly measures quantitative errors of the resulting tissue maps. A quantum-inspired optimization (QIO) approach is adopted to handle such non-convex and high dimensional problem. QIO has been shown to avoid the effects of local minima which means they can find the optimal sequences for a more flexible and realistic scan scenario, which is not feasible via classical optimization algorithms.Method
While the proposed framework could be applied to any MR sequence, we have started with an MRF-FISP sequence4. We constructed a cost function estimating T1 and T2 errors due to undersampling and measurement noise during the scan using a brain phantom with three representative tissue types, white matter, gray matter, and cerebrospinal fluid. The undersampling errors were modeled using a fast partially separable approach5. This approach alone achieved a factor of over 100 acceleration in computing aliasing artifacts from a highly accelerated single-shot spiral acquisition as compared to direct gridding. Quality factors were calculated to indicate the likelihood of corruption in signals of each tissue type in presence of random noise6. We adapted the substochastic Monte Carlo7, a quantum inspired optimization algorithm, and simulated annealing method8 to continuous variable problems and applied it to minimize T1 and T2 undersampling errors and maximize quality factors of all tissue types in each iteration. Accuracy and image quality of quantitative tissue maps were assessed using simulations and in vivo scans. For each sequence, signal evolutions from WM, GM and CSF of a phantom were simulated incorporating complex valued coil maps, then undersampled with a single shot spiral arm in k-space. The undersampled signal evolutions were matched to the MRF dictionary to obtain T1 and T2 values and compared against the ground truth. Separately, in vivo scans were performed in compliance with the IRB in a Siemens 3T Skyra scanner. Both the optimized and original empirical MRF sequences were tested on the same volunteer. All scans were acquired with an FOV of 300×300 mm2, image resolution of 1.2×1.2 mm2 using a single shot spiral acquisition, resulting in an acceleration factor of 48.Results
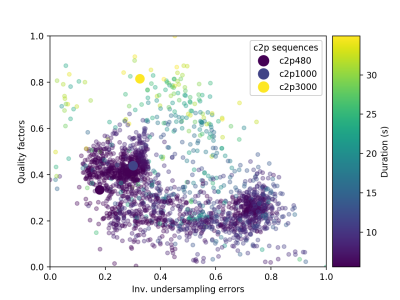
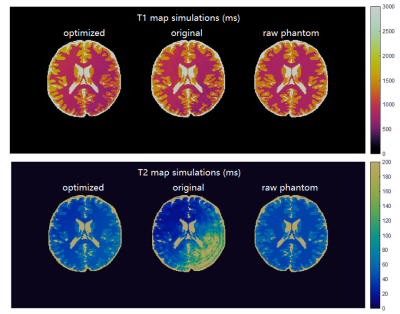
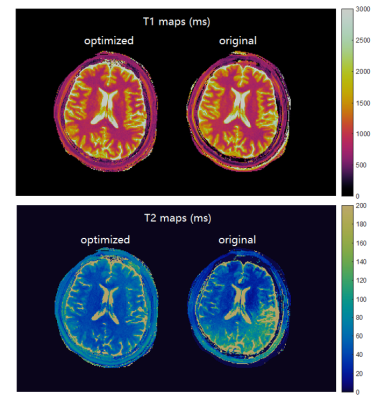
By evaluating wide ranges of hyperparameters in the cost function, QIO generated a large number of sequences with 480 TRs as mapped in Figure 1. Optimal solutions were identified via subsequent post-evaluation of quality factors, undersampling errors and scan time. Figure 2 shows the simulated T1 and T2 maps from one example of optimized sequence, the truncated original sequence (480 TRs) and raw phantom data. The simulated T2 map from the truncated original sequence exhibits severe shading artifacts similar to those in actual scans, and supported our simulation method as replicating in vivo conditions. In the simulation, maps from the optimized sequence are immune to the same undersampling and phase distortions. Table 1 lists T1 and T2 errors from three tissue types due to undersampling and noise. While the difference in mean T1 error between two sequences is not obvious, the mean T2 error is smaller for the optimized sequence. The acquisition time was slightly longer for the optimized MRF sequence of 6.4 s, as compared to 5.6 s from the truncated version of the original MRF sequence. Figure 3 demonstrates in vivo T1 and T2 scans from the same optimized sequence and the shortened original sequence (480 TRs). Similar to simulations, the T2 map from the optimized sequence shows no shading artifacts in frontal lobe and parietal lobe, thus provide more clear visualizations and more precise measurements of brain tissue structures.Conclusion
Using the proposed framework for MRF sequence optimization, we can optimize flip angle and TR patterns to restore signal orthogonality and robustness against aliasing and random errors present in MRF data acquisition. As this powerful framework facilitates great flexibility in non-linear cost function design, the optimization paradigm could integrate more sequence and tissue properties, or be modified based on signal features and real scan constrains for different MRF applications.Acknowledgements
The authors would like to acknowledge fundings from Siemens Healthineers, Microsoft and NIH grant EB026764-01 and NS109439-01References
1. Ma D, Gulani V, Seiberlich N, et al. Magnetic Resonance Fingerprinting. Nature. 2013;495(7440):187-192.
2. Cohen O, Rosen MS. Algorithm comparison for schedule optimization in MR fingerprinting. Magn Reson Imaging. 2017;41:15-21. doi:10.1016/j.mri.2017.02.010
3. Zhao B, Haldar JP, Liao C, et al. Optimal experiment design for magnetic resonance fingerprinting: Cramér-rao bound meets spin dynamics. IEEE Trans Med Imaging. 2019;38(3):844-861. doi:10.1109/TMI.2018.2873704
4. Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn Reson Med. 2015;74(6):1621-1631. doi:10.1002/mrm.25559
5. McGivney D, Boyacioglu R, Jordan S, et al. A Fast Approximation of Undersampling Artifacts in MR Fingerprinting. In: ISMRM Submitted. ; 2019.
6. Kara D, Fan M, Hamilton J, Griswold M, Seiberlich N, Brown R. Parameter map error due to normal noise and aliasing artifacts in MR fingerprinting. Magn Reson Med. 2019;81(5):3108-3123. doi:10.1002/mrm.27638
7. Jarret M, Lackey B. Substochastic Monte Carlo Algorithms. April 2017. http://arxiv.org/abs/1704.09014. Accessed October 23, 2019.
8. Kirkpatrick S, Gelatt CD, Vecchi MP.
Optimization by simulated annealing. Science (80- ).
1983;220(4598):671-680. doi:10.1126/science.220.4598.671
Figures