Purpose

Magnetic Resonance Fingerprinting¹ (MRF) has emerged as a highly promising technique for rapid multiparametric mapping in MRI. Besides the quantification of relaxation times, other parameters have been shown to benefit from an MRF-based quantification, among which is the quantification of flow velocities². This method, termed “Flow-MRF”, was shown to allow an approximately 2-fold acquisition time reduction compared to conventional velocimetry while simultaneously providing relaxometric maps of static tissues. However, this technique currently suffers from two major drawbacks: firstly a low efficiency since multiple shots are used and secondly strongly increased velocity noise for low velocities due to magnetization preparation pulses. This work targets both issues by presenting an optimized flip angle (FA)-pattern for Flow-MRF while assuming periodic boundary conditions as recently proposed³.

Background

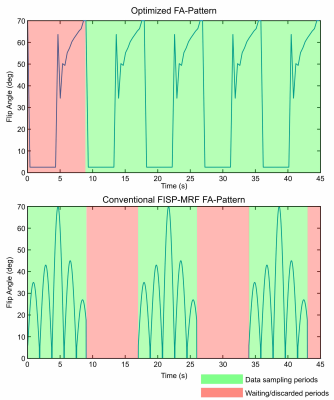
Flow-MRF acquires multiple repetitions ('multi-shot') of the MRF signal evolution while sampling different parts of k-space during each run. A delay in the order of 8-10s, depending on relaxation times, follows each FA-train repetition to allow the magnetization to approximately return to thermal equilibrium. While this delay can be used to sample other slices to achieve a 100% scan efficiency in multi-slice 2D MRF applications, this approach is unfeasible in 3D MRF or single-slice applications, and scan efficiency decreases to approximately 50% (see Fig.1). Therefore, continuously running MRF sequences have been proposed³, using periodic or anti-periodic boundary conditions of the magnetization between beginning and end of the FA-pattern³. Periodic boundary conditions seem particularly promising since they avoid the use of inversion preparation pulses, which causes increased velocity noise in Flow-MRF².

Methods

The FA optimization employs recently proposed quality metrics⁴, where both thermal and undersampling noise contributions are considered for parameter errors. The contributions of both noise sources was weighted according to phantom results obtained by a radial FISP sequence as described in [2] at 7T (Siemens, Germany). The ratio between undersampling to thermal noise levels was a factor of 8. The FA-pattern was optimized by minimizing the quality metrics to convergence with a generalized pattern search algorithm (patternsearch, MATLAB, USA) initialized with white noise. The FA-pattern length was fixed to 1000 but only 25 supporting points, equidistantly distributed over the FA-pattern, are optimized to reduce the dimensionally of the optimization problem. The remaining FAs are calculated by linear interpolation (see Fig.1). This optimization was performed for a representative isochromat with T₁=1500ms and T₂=60ms.
The sequence timings for the optimization are based on the 2D Flow-MRF sequence used in this work. Here, five radial shots were acquired per timeframe with TE/TR of 5.9/9.86ms. The first gradient moment (m₁) used to encode velocities varied from -30 to 30mT/m$$$\cdot$$$ms².
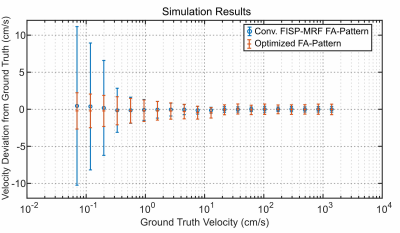
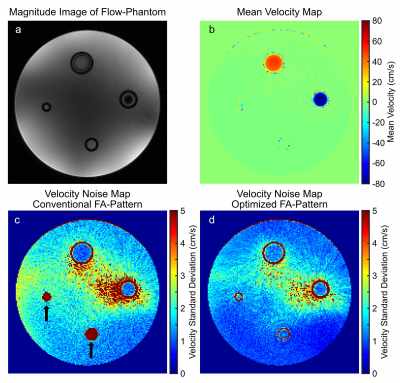
The influence of the proposed FA-pattern on velocity noise for low velocities (<5cm/s) and static tissue is investigated in both simulations and a phantom study. The simulations included spatial sampling and modeling of the fluid motion with velocities from 0.07cm/s to 14m/s. In the phantom experiment, the velocity noise was quantified in the static background and in flowing regions. Relaxation times were quantified in an agarose-gel-based phantom consisting of 13 tubes filled with varying agarose concentrations (0.75-2%) and doped with gadolinium-based contrast agent (0-0.1mmol/L).

Results

The lack of waiting periods in the optimized pattern yields a 1.58-fold increase in the readout efficiency as indicated in Fig.1. The first repetition of the optimized pattern is discarded as the magnetization's evolution differs from all other repetitions.
Simulation results (Fig.2) reflect a 4.3-fold reduction in velocity noise for velocities below 0.1cm/s using the optimized FA-pattern. For velocities >50cm/s, velocity noise increased from 0.3cm/s to 0.6cm/s. Note, that only the two largest tubes of this phantom are connected to the flow pump as seen in Fig.3b, while smaller tubes are filled with distilled water that was static. The optimized pattern clearly reduced the velocity noise in static tissue from 3.40cm/s to 1.86cm/s (see Fig. 3c-d). In particular, the conventional FA-pattern fails to quantify velocities in the smaller tubes due to the long T₁ of the distilled water, indicated by the black arrows in Fig.3c. Here, the mean velocity noise in these regions is 58.5cm/s. In flowing regions, a small velocity noise increase from 1.09cm/s to 1.22cm/s in flowing regions is measured for the proposed FA-pattern.
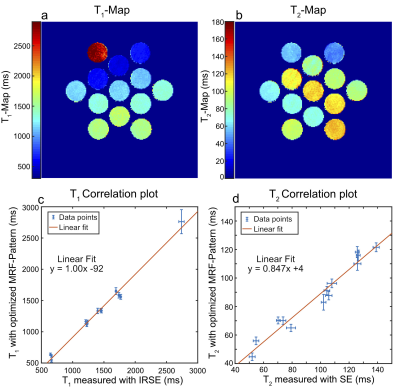
Fig.4 displays the relaxometric maps quantified by the optimized FA-pattern in the relaxation phantom. Despite the lack of inversion preparation, T₁ is well quantified based on the correlation to the reference. Nevertheless, an increase in the mean standard deviation in T₁ from 9.6ms for the conventional FA-pattern to 32ms was observed. Despite showing a strong linear correlation with the reference, T₂ values are systematically underestimated by 15.3% on average using the optimized pattern, which is not observed for the conventional FA-pattern.

Discussion

The optimization of FA-patterns for continuously running MRF sequences with periodic boundary conditions holds large potential for improving velocity quantification with Flow-MRF. These FA-patterns enable the possibility to efficiently measure Flow-MRF in large 3D volumes while strongly reducing noise in slow-flowing regions. The T₁ noise could potentially be compensated by the higher readout efficiency. The systematic bias in T₂ is subject to further investigations but might be related to an increased impact of magnetization transfer (MT) on the optimized FA-pattern.

Acknowledgements

No acknowledgement found.