3741
ST-UNet: Spatio-Temporal U-Net for Accelerating Simultaneous MultiSlice Magnetic Resonance Fingerprinting1University of North Carolina at Chapel Hill, Chapel Hill, NC, United States
Synopsis
In this study, a spatio-temporal U-Net was developed for efficient and accurate T1 and T2 quantifications from multislice MR Fingerprinting acquisitions. Our preliminary results demonstrate that the proposed method outperforms the standard template matching method and deep learning methods in the literature, enabling higher multislice factors for MR Fingerprinting.
Introduction
MR Fingerprinting (MRF) is a quantitative imaging technique that can provide fast and simultaneous quantification of multiple tissue properties (1). Compared to 2D MRF approaches, recent efforts have been devoted to improving the spatial coverage of the technique, and several methods utilizing simultaneous multislice acquisitions have been proposed (2-5). Due to the high in-plane acceleration factor applied in MRF (1), dramatic aliasing artifacts exist, which makes unalising along slice direction extremely challenging. With the existing methods, only limited multislice factors (2 or 3) were achieved and the image quality is suboptimal. Recently, several deep learning methods have been developed to replace the template matching approach to improve tissue characterization and acquisition speed (6-8). Most of these methods only consider either the spatial or temporal properties of the signal evolution, which limits its capability of extracting information from the complex MRF signals. In this study, we propose a new architecture: Spatio-Temporal UNet (ST-UNet), which exploits both spatial and temporal correlation of the MRF signal in order to achieve better image quality and higher multislice factors.Methods
All MRI measurements were acquired from a Siemens 3T scanner with a 32-channel head coil. A FISP-based multislice MRF method was developed and applied to five normal subjects (male, mean age, 29±7 years). Multiband RF pulses generated from SINC waveforms with phase modulations were used to excite multiple slices simultaneously (3). The same MRF acquisition patterns, including the variable flip angles and golden-angle spiral readouts, were applied to all excited slices. The slice thickness was 5 mm and the distance between adjacent slices was set at 10 mm. Similar to the original MRF framework, each MRF time frame was highly undersampled in-plane with only one spiral arm (reduction factor, 48). A total ~2300 MRF time frames were acquired and the acquisition time for each scan was 23 sec. Other imaging parameters included: FOV, 30×30 cm; matrix size, 256×256; MB factors, 3 or 4. Single-slice MRF acquisitions (10~12 scans for each subject) were also acquired for setting up the training dataset for our deep learning method as introduced below. After the MRF measurements, reference T1 and T2 maps were first extracted from the single-slice dataset using all 2300 time points with the pattern matching method (1). Simulated multislice MRF dataset, containing ~570 time points (25% of the total number of points), was then generated from the single-slice dataset with phase modulation to simulate the MB excitation pulse and used as the input data for network training (Fig. 1). The simulated multislice data from four subjects were used for training and the data from the remaining subject was used for validation. Separate networks were trained for each slice acquired in the multislice acquisition, considering different aliasing patterns across simultaneously excited slices. Fig. 2 shows the diagram of our deep learning network. Following (8), we first compress the high-dimensional time course of the MRF signals to a low-dimensional feature vector (64 features) via a 2D convolutional neural network with kernel size of 1x1. This allows extraction of useful features for the subsequent tissue quantification. A spatio-temporal U-Net (ST-UNet) is proposed for the following tissue property mapping, which exploits both the temporal nature of each fingerprinting and correlated information from the neighboring ones (Fig. 2). ST-UNet also follows an “encoder-decoder” architecture, but unlike conventional 3D UNet (9) , it factorizes the 3D convolution (k x k x t) into a 2D spatial convolution (k x k x 1) and a 1D temporal convolution (1 x 1 x t), where both k and t are 3 in our case. Such decomposition increases nonlinearities in the network due to the additional ReLU appended to the 2D convolution and potentially eases the optimization, while the total number of parameters is still comparable to that of a conventional 3D UNet by carefully choosing the number of kernels for the 1D/2D convolutions. After the training, the networks are applied to the acquired multislice MRF dataset and the results are compared with both ground-truth maps and the literature method (8).Results
Fig. 3 and Fig. 4 show representative results of obtained with a multislice factor of 3. The representative results with a factor of 4 are shown in Fig. 5 (only one slice is shown for ease of viewing). Compared with the results from template matching, deep learning methods significantly reduced the amount of aliasing artifacts. ST-UNet also outperformed the conventional 2D UNet on the actual acquired data for both T1 and T2, which suggests that more information are extracted with the proposed method, enabling higher multislice factors for MRF.Discussion and Conclusion
In this study, a spatio-temporal U-Net was developed for efficient and accurate T1 and T2 quantifications from multislice MRF acquisitions. While the simulated multislice data was used for training, this can be achieved by using actual acquired multislice data as input and ground-truth maps from single-slice acquisition as reference. The disadvantage of this approach is its high sensitivity to subject motion between the two scans. In this work, the same MRF acquisition patterns were applied to all excited slices. Future work will focus on varying acquisition parameters across slices to achieve better image quality and multislice factors (3).Acknowledgements
This work was supported in part by NIH grant EB006733.References
1. Ma D, et al. Nature, 2013; 187–192.
2. Ye H, et al. MRM, 2016; 2078-2085.
3. Jiang Y, et al. MRM, 2017; 1870-1876.
4. Ye H, et al. MRM, 2017; 1966-1974.
5. Hamilton J, et a;. NMR Biomed, 2019; e4041.
6. Cohen O, et al. MRM, 2018; 885-894.
7. Hoppe E, et al. ISMRM, 2018;p2791.
8. Fang Z, et al. IEEE TMI, 2019; 2364-2374.
9. Çiçek Ö, et al. Springer, Cham, 2016: 424-432.
Figures
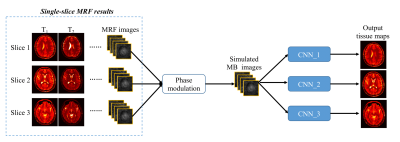


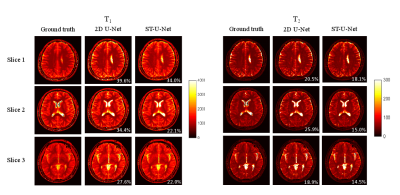
Figure 4. Representative T1 and T2 maps obtained from the actual acquired multislice MRF dataset (multislice factor, 3). The results were calculated using the CNN model trained with simulated MRF dataset. Both T1 and T2 maps simultaneously acquired from three slices in one MRF scan are presented.
