3740
Accelerated High-Resolution 3D MR Fingerprinting Using a Graph Convolutional Network1Department of Computer Science, University of North Carolina at Chapel Hill, CHAPEL Hill, NC, United States, 2CuraCloud Corporation, Seattle, WA, United States, 3Department of Radiology, University of North Carolina at Chapel Hill, CHAPEL Hill, NC, United States
Synopsis
In this study, a k-space interpolation technique for high-resolution 3D MR Fingerprinting is proposed. We formulate the problem as a graph and apply a graph convolutional network on the graph to interpolate the missing partitions. Our preliminary results show that the proposed method can provide improved results both in reconstructed k-space data and in extracted quantitative maps and can potentially allow higher acceleration factors along the partition-encoding direction.
Introduction
MR Fingerprinting (MRF) is a quantitative imaging framework for fast and simultaneous quantification of multiple tissue properties1. While most of the current studies focus on 2D MRF applications 2,3, 3D MRF provides higher SNR, improved spatial resolutions, and volumetric coverage and thus has drawn increasing attention from the community4. However, 3D MRF with high spatial resolution and covering a large volume requires extended imaging time that is too long for clinical applications. To address this concern, several methods have been proposed to accelerate 3D MRF acquisitions. Since the standard MRF approach is already highly undersampled in-plane with only one spiral arm acquired, most of the current methods4,5 utilize parallel imaging methods to accelerate along the partition-encoding direction. Due to the nature of non-Cartesian spiral acquisition6, conventional fast imaging methods 7,8 face challenges of low acceleration factors, poor image quality and lengthy reconstruction times. Deep learning methods9 are increasingly applied for Cartesian parallel imaging and have demonstrated improved performance compared with conventional parallel imaging approaches. Recently, graph theory has been integrated with deep learning methods10,11, capable of tackling tasks on non-Euclidean space. In this work, we propose a graph-based deep learning method to accelerate 3D MRF with stack-of-spirals trajectories. Our preliminary results suggest that a higher acceleration factor and an improved quantification accuracy can be achieved for high-resolution 3D MRF in neuroimaging.Methods
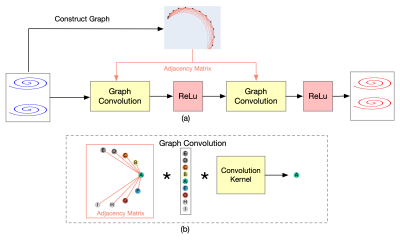
The MRI measurements were performed on a Siemens 3T Prisma scanner. A 3D MRF dataset from 6 subjects (M:F, 3:3; mean age, 34±10 years) was acquired. Each MRF time frame was highly undersampled in-plane with only one spiral arm (reduction factor, 48). The partition direction was linearly encoded and fully sampled. With a constant TR of 9.2 ms and a waiting time of 2 sec between partitions, the total scan time was ~11 min for each subject. Other imaging parameters included FOV, 25×25 cm; matrix size, 256×256 (effective in-plane resolution, 1 mm); slice thickness, 1 mm; number of slices, 144; variable flip angles, 5°~12°; MRF time frame, 192.An interleaved sampling pattern introduced by Ma et al.4 was used to undersample data in the partition direction. We aimed to reconstruct the skipped partitions from the nearest two acquired partitions as shown in Fig. 1. Fig. 2 shows the structure of the network. Given the non-Cartesian nature of spiral trajectories, we first represent the in-plane trajectories as algebraic graphs. The weights of the graph adjacency matrix are defined as the negative exponential of the square of normalized Euclidean distances between points in the spiral readout direction. Two graph-convolutional layers11 are then applied for convolution of non-uniformly distributed points in the non-Cartesian spiral acquisition. A ReLU layer is applied after each graph-convolutional layer for nonlinear mapping.
The network was trained with the central 12 partitions of 5 subjects with one remaining subject for testing. The MSE loss was adopted as the objective function. Gradient descent optimization was performed using Adam12 with an initial learning rate of 0.0001, which was reduced by 98% for every 3 epochs. The k-space data were normalized such that the maximum absolute value was 0.15 along the $$$mrf\ frame \times partition \times coil$$$ dimensions. Acceleration factors 2 and 3 along the partition direction were examined. NMSE was calculated for both reconstructed k-space data and quantitative T1 and T2 maps. The results were further compared with those from the standard GRAPPA reconstruction13, 14.
Results
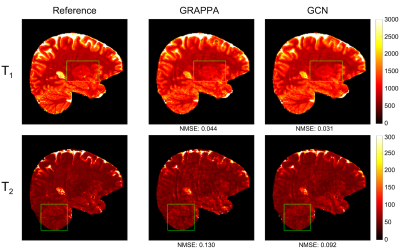
Figs. 3 and 4 show the representative quantitative T1 and T2 maps obtained with acceleration factors 2 and 3, respectively. Compared with the ground-truth maps, the quantitative maps from the proposed method are less noisy and contain fewer artifacts than those from GRAPPA. Compared with the GRAPPA reconstruction, the NMSE values (Fig. 5) given by the proposed method are much lower for both the reconstructed k-space data and quantitative T1 and T2 maps. All these results suggest that the proposed method can achieve higher acceleration and improved accuracy than conventional parallel imaging methods.Discussion and conclusion
The overall goal of our study is to develop a rapid and high-resolution 3D MRF technique for whole-brain quantitative imaging. A two-step processing scheme has been previously proposed, which includes GRAPPA reconstruction along partition-encoding direction and deep learning modeling for efficient tissue characterization14. In this study, the GRAPPA reconstruction was replaced with a graph-based deep learning k-space interpolation technique. Our preliminary results demonstrate that the proposed method can cope with non-Cartesian reconstruction with higher acceleration. Only 192 time frames were acquired in each scan for rapid quantitative imaging. Thousands of time frames were acquired in earlier studies1, 5. While some residual artifacts were noticed, especially with the acceleration factor 3, the performance can be significantly improved when integrated with a deep-learning tissue characterization technique2, 14. In addition, the time (~3min) to reconstruct one 3D MRF case with the trained network is about 30 times faster than conventional GRAPPA reconstruction. Future work will focus on the integration of k-space reconstruction and tissue quantification to enable rapid data acquisition, high-quality quantification and efficient post-processing for high-resolution quantitative imaging.Acknowledgements
This work was supported in part by NIH grant EB006733.References
1. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL and Griswold MA. Magnetic resonance fingerprinting. Nature. 2013;495(7440): 187.
2. Fang Z, Chen Y, Liu M, Xiang L, Zhang Q, Wang Q, Lin W, and Shen D. Deep Learning for Fast and Spatially-Constrained Tissue Quantification from Highly-Accelerated Data in Magnetic Resonance Fingerprinting. IEEE transactions on medical imaging. 2019;38(10):2364-2374.
3. Fang Z, Chen Y, Nie D, Lin W, and Shen D. RCA-U-Net: Residual Channel Attention U-Net for Fast Tissue Quantification in Magnetic Resonance Fingerprinting. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 101-109. Springer, Cham, 2019.
4. Ma D, Jiang Y, Chen Y, McGivney D, Mehta B, Gulani V and Griswold M. Fast 3D magnetic resonance fingerprinting for a whole‐brain coverage. Magnetic resonance in medicine. 2018; 79(4): 2190-2197.
5. Liao C, Bilgic B, Manhard M K, Zhao B, Cao X, Zhong J and Setsompop K.. 3D MR fingerprinting with accelerated stack-of-spirals and hybrid sliding-window and GRAPPA reconstruction. Neuroimage. 2017;162: 13-22.
6. Wright KL, Hamilton JI, Griswold MA, Gulani V and Seiberlich N. Non‐Cartesian parallel imaging reconstruction. Journal of Magnetic Resonance Imaging. 2014; 40(5): 1022-1040.
7. Heidemann RM, Griswold MA, Seiberlich N, Krüger G, Kannengiesser SA, Kiefer B and Jakob PM. Direct parallel image reconstructions for spiral trajectories using GRAPPA. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2006; 56(2): 317-326.
8. Seiberlich N, Lee G, Ehses P, Duerk JL, Gilkeson R, and Griswold M. Improved temporal resolution in cardiac imaging using through‐time spiral GRAPPA. Magnetic resonance in medicine 66, no. 6 (2011): 1682-1688.
9. Akçakaya M, Moeller S, Weingärtner S and Uğurbil K. Scan‐specific robust artificial neural networks for k‐space interpolation (RAKI) reconstruction: Database‐free deep learning for fast imaging. Magnetic resonance in medicine. 2019;81(1): 439-453.
10. Defferrard M, Bresson X and Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in neural information processing systems. pp. 3844-3852. 2016.
11. Kipf TN and Welling M. Semi-supervised classification with graph convolutional networks. In ICLR, 2017.
12. Kingma DP and Ba J. Adam: a Method for Stochastic Optimization. In International Conference on Learning Representations. pp. 1–13. 2015.
13. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2002 47(6): 1202-1210.
14. Chen Y, Fang Z, Shen D and Lin W. High-resolution 3D MR Fingerprinting using parallel imaging and deep learning. NeuroImage. 2019. In press.
Figures