3736
Retrospective motion correction of three-dimensional Magnetic Resonance Fingerprinting (MRF)1Imago7, Pisa, Italy, 2INFN, Pisa, Italy, 3University of Pisa, Pisa, Italy, 4Technical University of Munich, Munich, Germany, 5GE Healthcare, Munich, Germany, 6Neuroradiology, Azienda Ospedaliero-Universitaria Pisana, Pisa, Italy, 7IRCCS Stella Maris, Pisa, Italy
Synopsis
We demonstrate a novel motion correction of 3D magnetic resonance fingerprinting (MRF) using spiral projection k-space trajectory. The motion was corrected using rigid motion parameters extracted from a whole-brain navigator obtained every 7s of imaging. Firstly, we optimized the trajectory ordering in simulation and selected the acquisition scheme that allowed the best navigator for motion correction. Secondly, we applied this scheme to invivo data in healthy subjects scanned first without motion and then while performing a motion paradigm. Our motion correction improved the correlation of motion-corrupted data with motionless data by over 20% for both T1 and T2.
Introduction
One of the major challenges in MRI data quality are artefacts caused by subject’s movements. Several approaches for motion correction have been developed1–3, however there is no universal solution and motion correction remains an open problem, especially when examining children4, elderly people or populations that are prone to extreme motion. Magnetic resonance fingerprinting (MRF) has been demonstrated for the estimation of multiple quantitative parameters in a single scan. MRF data can be acquired in a short time, are less sensitive to motion and system imperfections, and have high quantification accuracy, repeatability and reproducibility5,6. However, with significant motion, some issues remain. Several solutions for characterizing or improving the motion-corrupted 2D MRF data have been suggested7,8, but motion correction for 3D MRF still requires investigation. Here, we aimed at performing a novel navigator-based retrospective motion correction on three-dimensional, whole brain imaging based on spiral projection k-space trajectories.Methods
Data acquisition and reconstruction: Our work was based on a recently proposed 3D SSFP MRF using variable density spiral projection trajectory9. We compared different orderings of trajectory interleaves (shown in Figure 1A) in terms of motion robustness. In all tested orderings we considered the dataset as a sum of 56 segments (each reconstructed from 880 spiral interleaves) acquired sequentially with the same flip angle train (shown in Figure 1B), each preceded by an adiabatic inversion pulse. Our trajectories had a total number of 49280 interleaves, each consisting of 876 readout points acquired at a 250 kHz bandwidth. Data were acquired with a FOV of 225x225x225 mm and reconstructed with a matrix size of 200x200x200. Acquisition TE/TR were 0.5ms/8.5ms, respectively, resulting in a total scan time of 7 minutes. SVD-based reconstruction10 was performed, retaining the first 10 singular values. Parameter inference was performed on inner-product pattern matching with a precomputed dictionary as described in11.Navigator-based retrospective motion correction: We performed a separate image reconstruction for each segment producing 56 whole-brain volumes. The registration of the data was performed using normalised correlation coefficient (using SPM1212) on the first singular value image, extracting segment-wise rotations and translations, to then be applied to each acquired segment in k-space. The motion-corrected segments were then summed prior to dictionary matching.
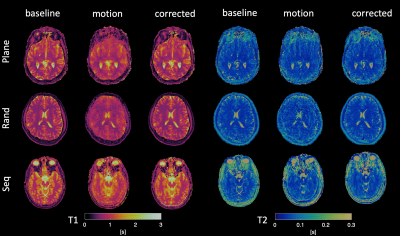
Motion simulation: To evaluate the alignment capabilities for our algorithm, motion was simulated on a motion-free dataset for all three trajectory orderings tested. The different trajectory orders are shown in Figure 1A. The motion estimations from different trajectory orders were compared and the one with the highest performance was chosen for the next experiments.
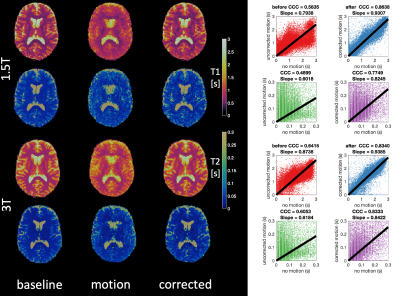
In vivo test of motion correction: We acquired data from ten healthy subjects. Participants were instructed to stay still during the first acquisition, while in a second one they were advised to change the position of their head about 10 times during the 7 min scan. All subjects were acquired both on a GE HDxt 1.5T scanner (GE Healthcare, Chicago, IL) and on a GE MR750 3.0T scanner (GE Healthcare, Chicago, IL). To compare the quantitative maps we used voxel-wise CCC (concordance correlation coefficient)13. In all comparisons the motionless data was used as the reference dataset.
Results
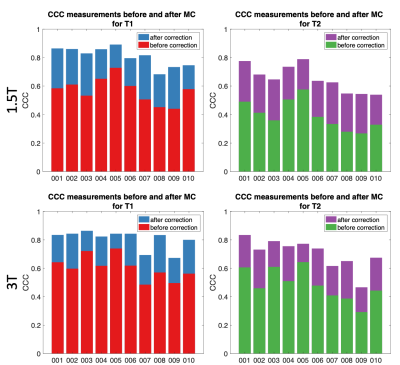
Motion Simulation: Although we simulated exactly the same motion with all three orderings, the one with random permutations resulted in the highest CCC for both T1 and T2, as shown in Figure 2. This was also confirmed by visual inspection of the quantitative maps.Real motion data: As in the case of simulation, CCC is estimated for motion-affected and motion-corrected dataset. Data from a representative subject for both 1.5T and 3.0T is shown in Figure 3. A significant improvement on the motion-affected maps after motion correction is evident, however, some residual artefacts remain especially on the T2 maps. Motion artefacts are present similarly to the simulation before the correction and were clearly reduced after applying the motion correction routine, as shown both by quantitative analysis and visual inspection. Group analysis describing the improvement of the CCC for all ten subjects are shown in Figure 4, while the improvement of the CCC in each individual subject is shown in Figure 5. The improvement of CCC after motion correction was 20% on average for both T1 and T2 estimations
Discussion
We demonstrated a method that allows correcting 3D motion during the reconstruction of MRF data using self-navigators. By dividing the entire dataset in 7s-long segments, we gained sufficient temporal resolution to realign the dataset. Although the in-vivo data was well aligned some artefacts still remained, possibly due to phase inconsistencies or undersampling artefacts after the alignment. A main limitation of the technique is that currently it can only correct for involuntary motion on a 10s scale, but not motion on a faster scale like physiological motion.Conclusions
In conclusion, motion-corrected 3D MRF scan features fully-quantitative data and a reduced sensitivity to motion without additional acquisition, and can be used to acquire an anatomical exam in 7 minutes at a standard resolution for clinical examination.Acknowledgements
Work was supported by the Italian Ministry of Health and the Tuscany Region under the project “Ricerca Finalizzata”, Grant n. GR-2016-02361693.References
1. Godenschweger, F. et al.Motion correction in MRI of the brain. Phys. Med. Biol.(2016) doi:10.1088/0031-9155/61/5/R32.
2. Maclaren, J., Herbst, M., Speck, O. & Zaitsev, M. Prospective motion correction in brain imaging: A review. Magn. Reson. Med.(2013) doi:10.1002/mrm.24314.
3. Zaitsev, M., Maclaren, J. & Herbst, M. Motion artifacts in MRI: A complex problem with many partial solutions. Journal of Magnetic Resonance Imaging(2015) doi:10.1002/jmri.24850.
4. Brown, T. T. et al.Prospective motion correction of high-resolution magnetic resonance imaging data in children. Neuroimage(2010) doi:10.1016/j.neuroimage.2010.06.017.
5. Buonincontri, G. et al.Multi-site repeatability and reproducibility of MR fingerprinting of the healthy brain at 1.5 and 3.0 T. Neuroimage(2019) doi:10.1016/j.neuroimage.2019.03.047.
6. Jiang, Y. et al.Repeatability of magnetic resonance fingerprinting T1 and T2 estimates assessed using the ISMRM/NIST MRI system phantom. Magn. Reson. Med.(2017) doi:10.1002/mrm.26509.
7. Cruz, G., Jaubert, O., Schneider, T., Botnar, R. M. & Prieto, C. Rigid motion-corrected magnetic resonance fingerprinting. Magn. Reson. Med.(2019) doi:10.1002/mrm.27448.
8. Yu, Z. et al.Exploring the sensitivity of magnetic resonance fingerprinting to motion. Magn. Reson. Imaging(2018) doi:10.1016/j.mri.2018.09.002.
9. Cao, X. et al.Fast 3D brain MR fingerprinting based on multi-axis spiral projection trajectory. Magn. Reson. Med.(2019) doi:10.1002/mrm.27726.
10. McGivney, D. F.et al.SVD compression for magnetic resonance fingerprinting in the time domain. IEEE Trans. Med. Imaging(2014) doi:10.1109/TMI.2014.2337321.
11. Dan Ma, Vikas Gulani, Nicole Seiberlich, Kecheng Liu, Jeffrey L. Sunshine, Jeffrey L. Duerk, aMark A. G. Magnetic Resonance Fingerprinting Dan. Nature(2013) doi:10.1002/mp.13078.
12. Penny, W., Friston, K., Ashburner, J., Kiebel, S. & Nichols, T. Statistical Parametric Mapping: The Analysis of Functional Brain Images. Statistical Parametric Mapping: The Analysis of Functional Brain Images(2007). doi:10.1016/B978-0-12-372560-8.X5000-1.
13. Lin, L. I.-K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics(1989) doi:10.2307/2532051.
Figures