Introduction

Multi-echo gradient echo (MEGRE) sequences are a common tool in MRI with a variety of applications such as R₂^*- and quantitative susceptibility mapping (QSM). For other multi-contrast MRI sequences, strong acceleration can be achieved by exploiting correlations between the temporal signals for different tissue parameters. This translates into a low-rank constraint for the Casorati matrix of the images to be determined [1]. As a matter of fact, aforementioned low rank-property does not hold for MEGRE images due to the B₀-induced time evolution of the image phase. Here we demonstrate that spatio-temporal correlations can be exploited when considering local image patches. As a result, we formulate image reconstruction as a locally low rank regularized (LLR) inverse problem [2,3] and show its effectiveness in comparison to standard compressed-sensing reconstructions.

Methods

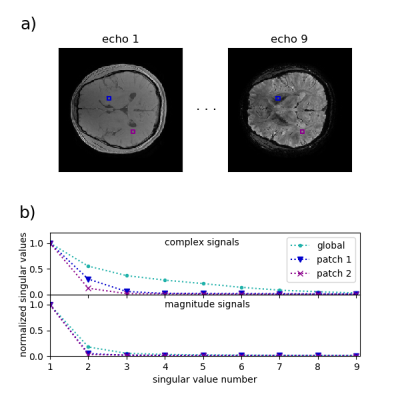
In MEGRE MRI , the magnitude signal in a given voxel shows an approximately exponential decay. However, B₀-inhomogeneity leads to a temporally oscillating phase, which makes it hard to find a low rank representation for the different signal evolutions in the image series. On the other hand, voxels within a small patch typically experience similar values of inhomogeneity, which makes it possible to find a low rank representation. To demonstrate this, we used the in-vivo brain dataset (measured on a GE scanner) accompanying the MEDI toolbox [4,5]. Fig. 1 shows the normalized singular values of both the global Casorati matrix and the Casorati matrix for two image patches. The former also suggests that a representation with lower rank can be found for signals similar to the magnitude signal. Based on those observations, we formulate the following reconstruction problem
$$ \underset{\mathbf{x}}{\operatorname{argmin}} \parallel \mathbf{y}-\mathbf{E}\mathbf{\Phi}\mathbf{x} \parallel_2^2 + \lambda\sum_{\mathbf{r}} L(R_{\mathbf{r}}\mathbf{x})$$
Here $$$\mathbf{E}$$$ denotes the signal encoding operator and $$$\mathbf{y}$$$ denotes the measured k-space signal. Analogously to [1], $$$R_{\mathbf{r}}$$$ extracts blocks around location $$$\mathbf{r}$$$ and reshapes them into the columns of the associated Casorati matrix. As a surrogate of the rank, $$$L$$$ denotes the logdet penalty of the singular-values, which was proposed in [4]. Although being non-convex the latter was observed to show superior results compared to the convex nuclear norm. Finally, we include the diagonal operator $$$\mathbf{\Phi}$$$ which multiplies each entry in $$$\mathbf{x}$$$ with an estimate of the image phase for the associated voxel and echo. As discussed before, this leads to a more compact representation of the spatio-temporal signals. In summary, the proposed method starts by solving (1) for $$$\mathbf{\Phi}_0 = \mathbf{1}$$$. Then the solution can be refined by updating the phase estimate $$$\mathbf{\Phi}_1$$$ and solving the new form of problem (1). In order to test the proposed method, the complex-valued brain dataset used before was Fourier transformed into k-space. The data was retrospectively undersampled using a variable density poisson disk pattern with a fully sampled calibration area of size 24x24. Finally, the multi contrast image series was reconstructed using the proposed method with and without updating the phase estimate. For comparison we also performed a compressed sensing (CS) reconstruction with ℓ₁ regularization in the Wavelet domain.

Results

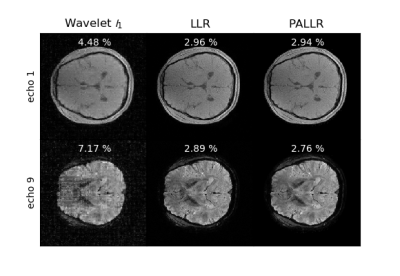
Fig. 2. shows the reconstructed magnitude images for the first and the last echo of the image series. The Wavelet-based CS reconstruction shows blurring and severe artifacts. For the proposed method, the reconstruction quality is increased. This is also reflected in the normalized root mean squared deviation (NRMSD), which is shown in the figure for each contrast. Incorporating the image phase into the imaging operator, leads to a further reduction in NRMSD and a reduced amount of perceivable noise.

Discussion

Our results demonstrate that LLR regularization is a powerful prior for the reconstruction of MRGRE image data. This can be justified by the fact that the underlying B₀ map typically has a smooth structure. As a consequence neighboring voxels show a similar oscillatory behavior. By incorporating a prior phase estimate into the imaging operator, the images to reconstruct show more resemblance to the magnitude signals, which explains the additional increase in reconstruction quality. Note that the reconstruction problem (1) can be solved efficiently using ADMM [6]. Moreover, the successive reconstructions can be initialized with the previous image estimate. Thus, obtaining a phase estimate only leads to a moderate increase in reconstruction time.

Conclusion

A new image reconstruction was developed, which exploits signal correlations through LLR regularization. In particular, this method is suited for MEGRE sequences, where the image signals are no longer contained in a global low rank subspace. In comparison to standard CS methods, it allows successful image reconstruction at larger undersampling factors. Thus, the proposed method has the potential to further accelerate MRI applications such as R₂^*-mapping and QSM.

Acknowledgements

No acknowledgement found.