3728
Magnetic Resonance Imaging Using Multiple-leaf Smoothed Random-like Trajectory
Haifeng Wang1, Yuchou Chang2, Xin Liu1, Hairong Zheng1, and Dong Liang1
1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2University of Houston-Downtown, Houston, TX, United States
1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2University of Houston-Downtown, Houston, TX, United States
Synopsis
Smoothed Random-like Trajectory (SRT) is a promising MR imaging method, but the data acquisitions have some hardware limitations of the gradient amplitude and slew rate. In order to realize the SRT in k-space, we proposed a new multiple-leaf SRT in k-space to reduce hardware requirements for applying the Compressed Sensing (CS) theory. To guarantee the constrains of the gradient amplitude and slew rate and reduce readout, the proposed multiple-leaf gradient waveforms were optimized by the time-optimal method for arbitrary k-space trajectories. The simulations have showed that the proposed method could greatly improve the reconstruction image quality, comparing to spiral trajectories.
Introduction
Recently, many research results 1-11 have found that it could improve reconstructions to add random perturbed factors into the conventional sampling trajectories. Their results have showed that using randomly perturbed k-space trajectories enables more sparsely sampled image reconstruction with higher quality and fewer artifacts compared to using non-randomly sampled trajectories in CS MRI, because of satisfying the RIP condition 12-13. The sampling trajectories, such as, Radial and Spiral, can directly be reconstructed by the CS framework 14-15. However, random trajectories sampling in frequency domain is impractical for MRI hardware. Previously, single-leaf random-like trajectory (SRT) has been proposed to better apply the CS framework to reconstruct images than before 8. To obey the hardware limitations and reduce readout for acquisition feasibility, we propose a scheme to generate a multiple-leaf SRT to satisfy the RIP condition 12-13. Firstly, the random-like trajectory per leaf is created based on the high order Chirp (HOC) sequences 8,16. Secondly, the Traveling Salesman Problem (TSP) solver 17-18 is applied to choose a “short” trajectory per leaf. Thirdly, we use a fast algorithm to design a time optimal gradient waveforms to obey the gradient amplitude and slew rate limitations per leaf 19. Fourthly, non-uniform fast Fourier transformation (NUFFT) 20 and nonlinear conjugate gradient (CG) 14-15 are used together by all leaves to reconstruct under the CS framework. The simulation results show the proposed multiple-leaf SRT can reduce artifacts than the conventional Spiral under the CS framework.Theory
The CS theory allows sparse or compressible signals to be sampled at a rate that is close to their intrinsic information rate and well below their Nyquist rate, and still allows the signal to be recovered exactly from randomly under-sampled frequency measurements by a non-linear procedure12-15. And the HOC sequences are that a family of discrete sequences have the special “random-like” uniformly decaying auto-correlation properties 16. The HOC sequences can satisfy RIP property 12-13 under some conditions 16. A sequence of numbers from the HOC sequences has been defined as,$$ u(t)=\frac{t}{\beta}\cdot e^{i\cdot2\alpha\pi t^{3}} , (1) $$
where, β is the decay coefficient;α is a random coefficient; t increases from 0 to β. Based on the sequence numbers from Eq.(1), one leaf of multiple-leaf SRT is generated by,
$$ s(t)=|u(t)|\cdot e^{i\cdot \theta(u(t))\cdot{2\pi} /L} , (2) $$
where, |.| is the magnitude values of complex numbers; θ(.) is the angle function of complex numbers; L is the leaf number. Based on Eq.(1), the multiple-leaf SRT can be generated by several leaves from Eq.(2). But now, this trajectory cannot satisfy the maximum gradient and slew rate limitations, to be implemented by the pulse sequences on MRI scanners. The proposed multiple-leaf SRT is illustrated as seen as Figure 1. Here, the TSP solver with the Simulated Annealing (SA) algorithm 17,18 has been applied to traverse the sampling points. And the algorithm based on optimal control theory 8,19 is applied to compute the time-optimal gradient waveform of the paths after the TSP traverse. The sampling points of the proposed multiple-leaf SRT are one type of non-Cartesian sampling, which can be reconstructed by NUFFT 20 and nonlinear CG 14-15 algorithms under the CS framework.
Methods
The two in vivo human brain data were acquired on a 3T uMR 790 system (United Imaging Healthcare, Shanghai, China) by the fast spin echo sequences (FOV: 230×200mm; TE/TR: 93.4/3800s; Resolution: 0.9mm; Thickness: 5mm) with a commercial 36-channel head coil. Both of the data sizes were 256×256. The 4736 and 4735 points were sampled on the Spiral and proposed trajectories, as seen as Figure 2. The total 4736 and 4735 points of Spiral (Figure 2a) and the proposed multiple-leaf SRT (Figure 2b) have been sampled respectively. The proposed multiple-leaf SRT has 5 leaves; the one-leaf gradient magnitudes have the maximum gradients of 0.55 Gauss/cm; the one-leaf slew-rate magnitudes have the maximum value of 15 Gauss/cm/ms. All reconstruction calculations were running on the MATLAB 2016a (MathWorks Inc., Natick, Massachusetts, USA). Here, the workstation platform has CPU of AMD Athlom(tm) 7750 Dual-Core (2.7G Hz); RAM of 8 GB; OS of Microsoft Windows 7 Professional 64-bit.Results
Figure 3 and 4 are comparing the reference and images reconstructed by the CS framework with L-1 minimization, total variance (TV) terms and sparse transformation 14-15 between the Spiral and proposed trajectories from Figure 2. The results illustrated that the proposed method could improve the image quality, comparing to the Spiral method. Especially, the proposed method could greatly remove the wrap-around and other types of artifacts, in comparison to existing Spiral sampling strategies. The aliasing artifacts of the proposed method were close to some random noise. The proposed multiple-leaf strategy could effectively reduce readout length for actual acquisition feasibility.Conclusion
In sum, we propose a novel trajectory scheme for reconstructions under the CS framework. The current results show the proposed trajectory outperforms the conventional Spiral trajectory in reducing aliasing artifacts. Based on the current results, the proposed method is able to effectively enhance reconstruction performance in the application context of CS recon framework and reduce readout for feasibility. In the future, more actual experiments on the scanners will be done to validate the proposed multiple-leaf SRT method.Acknowledgements
This work was partially supported by the National Natural Science Foundation of China (61871373, 81729003, and 61471350), the Natural Science Foundation of Guangdong Province (2018A0303130132), the Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000), the Shenzhen Peacock Plan Team Program (KQTD20180413181834876), the Shenzhen Key Laboratory of Ultrasound Imaging and Therapy (ZDSYS20180206180631473) and the Sanming Project of Medicine in Shenzhen (SZSM201812005).References
- Lustig M, et al. Faster imaging with randomly perturbed undersampled spirals and L1 reconstruction. Proc of the ISMRM. Miami, FL USA, May 2005.
- Chang T, et al. MR image reconstruction from sparse radial samples using Bregman iteration. Proc of the ISMRM, Seattle, WA, USA, May 2006.
- Bilgin A, et al. Randomly perturbed radial trajectories for compressed sensing MRI. Proc of the ISMRM, Seattle, Toronto, Canada, May 2008.
- El-Metwally S, et al. Rapid cardiac MRI using random Radial trajectories. Proc of the NRSC, Tanta, Egypt, Mar. 2008.
- Curtis A, et al. Random volumetric MRI trajectories via genetic algorithms. Int. J. of Biomed. Imaging, 2008(2008): 297089, 2008.
- Seeger M, et al. Optimization of k-space trajectories for compressed sensing by Bayesian experimental design. Magn Reson Med. 63(1): 116-126, 2010.
- Willett R. Sampling trajectories for sparse image recovery. Proc. of IEEE ISBI, Chicago, IL, USA, Jun. 2011.
- Wang H, et al. Smoothed random-like trajectory for compressed sensing MRI. Proc. of IEEE Eng Med Biol Soc. 2012: 404-407, 2012.
- Chauffert N, et al. Variable density sampling with continuous trajectories. SIAM J Imaging Sci. 7(4): 1962–1992, 2014.
- Lazarus C, et al. SPARKLING: variable‐density k‐space filling curves for accelerated T2*-weighted MRI. Magn Reson Med. 81(6): 3643-3661, 2019.
- Weiss T, et al. PILOT: Physics-Informed Learned Optimal Trajectories for Accelerated MRI. arXiv, 1909: 05773, 2019.
- Candès EJ, et al. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inform Theory. 52: 489-509, 2006.
- Donoho D. Compressed sensing. IEEE Trans Inform Theory. 52: 1289-1306, 2006.
- Lustig M, et al. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 58: 1182-1195, Dec. 2007.
- Lustig M, et al. Rapid MR imaging with compressed sensing and randomly undersampled 3DFT trajectories. Proc of the ISMRM, Seattle, WA, USA, May 2006.
- Saligrama V. Deterministic designs with deterministic guarantees: Toeplitz compressed sensing matrices, sequence design and system. arXiv, 0806: 4958, 2008.
- Kirkpatrick S, et al. Optimization by Simulated Annealing. Science, 220(4598): 671-680, 1983.
- Černý V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J Optim Theory Appl. 45: 41-51, 1985.
- Lustig M, et al. A fast method for designing time-optimal gradient waveforms for arbitary k-space trajectories. IEEE Trans Med Image. 27(6): 866-873, 2008.
- Fessler J. On NUFFT-basesd gridding for non-Cartesian MRI. J Magn Reson, 188: 191-195, 2007.
Figures
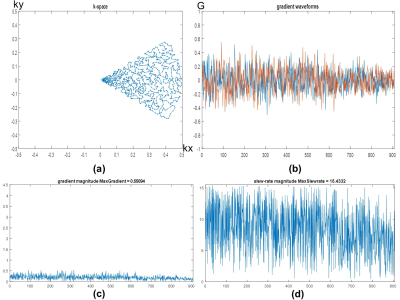
Figure 1. One-leaf trajectory and
gradient waveforms of the proposed multiple-leaf SRT method. (a)
is one-leaf trajectory of multiple-leaf SRT (5 leaves);
(b) is the gradient waveforms of one-leaf trajectory;
(c) is the one-leaf gradient magnitudes with the
maximum gradients of 0.55 Gauss/cm; (d) is the one-leaf
slew-rate magnitudes with the maximum value of 15 Gauss/cm/ms.
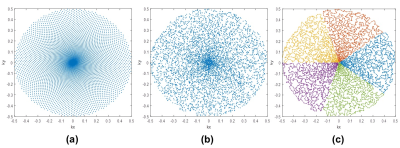
Figure 2 Trajectories comparison of Spiral and the
proposed multiple-leaf SRT method. The
total 4736 and 4735 points of Spiral (a) and the proposed multiple-leaf SRT (b) have been sampled respectively. (c)
illustrates the proposed multiple-leaf SRT with 5 leaves.
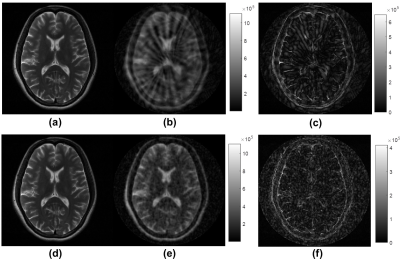
Figure 3. Comparison of the reference images from
human brain (a and d), CS reconstruction results (b and e) from the trajectories in Figure 2 (b is from Spiral, and e is from the proposed
multiple-leaf SRT method) and difference maps from the reference images (c and
f) of Spiral (c) and the proposed multiple-leaf SRT method (f)
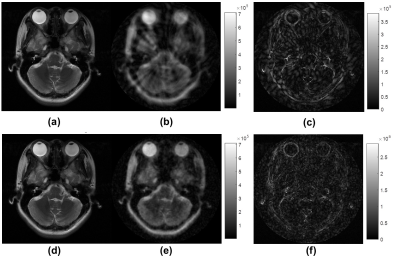
Figure 4. Head comparison of the reference images
(a and d), CS reconstruction results (b and e) from the trajectories in Figure
2 (b is from Spiral, and e is from the proposed multiple-leaf SRT method) and
difference maps from the reference images (c and f) of Spiral (c) and the proposed
multiple-leaf SRT method (f)