3723
Unbalanced SSFP for Ultra-High Field Super-Resolution MRI
Peter J Lally1, Paul M Matthews1,2, and Neal K Bangerter3
1Department of Brain Sciences, Imperial College London, London, United Kingdom, 2UK Dementia Research Institute, London, United Kingdom, 3Department of Bioengineering, Imperial College London, London, United Kingdom
1Department of Brain Sciences, Imperial College London, London, United Kingdom, 2UK Dementia Research Institute, London, United Kingdom, 3Department of Bioengineering, Imperial College London, London, United Kingdom
Synopsis
Here we exploit the off-resonance profile of the steady-state free precession (SSFP) sequence to encode spatial information with ultra-low flip angle radiofrequency pulses, enabling a super-resolution reconstruction from a rapid series of low-resolution images. This opens up new possibilities for rapid, high-resolution and low specific absorption rate (SAR) SSFP imaging, particularly at ultra-high magnetic field strengths.
Introduction
The drive towards ultra-high field MRI is largely motivated by increases in signal-to-noise ratio (SNR), but rapid high-resolution imaging with steady-state free precession (SSFP) sequences is typically avoided due to the presence of excessive banding artifacts, and restrictions on radiofrequency (RF) pulse flip angles due to specific absorption rate (SAR) concerns.This work instead exploits the characteristic off-resonance profile of SSFP sequences at ultra-low flip angles to achieve super-resolution MRI with minimal RF power requirements. This allows us to surpass practical restrictions on spatial resolution, enabling rapid, high-resolution imaging at ultra-high fields, while maintaining reasonable SNR.
Theory
The off-resonance profile in SSFP imaging in a homogeneous medium is well described, and has a periodicity of 2/TR. In the limit of small flip angles (α<3°) the magnitude of this approximates a damped comb function, with peaks at the points of rapid phase transition every 1/TR (Figure 1).An unbalanced linear magnetic field gradient causes a periodic modulation of the magnetisation along one dimension of the object, with the magnitude of the steady state signal concentrated in peaks at the points of rapid phase transition. These points correspond to the regions where banding artefacts are observed on higher flip angle balanced SSFP acquisitions. This periodic modulation can be made to coincide with the voxel spacing by ensuring that the unbalanced gradient has an area of $$$2k_{max}$$$ per excitation (e.g., in the phase encode direction, Figure 2), where $$$k_{max}$$$ is the maximum spatial frequency encoded in the traditional Fourier way. As a result, the signal from each voxel is predominantly derived from spins near the centre of the voxel in the locality of the peak in the off-resonance profile.
By applying a phase increment, Δφ, between successive RF excitation pulses, the off-resonance signal profile induced across each voxel (or 'intravoxel profile') can be shifted along the unbalanced gradient direction. Over a series of N acquisitions, each with an increasing RF excitation phase increment, a set of low-resolution images is acquired, each containing unique high-resolution information about the intravoxel magnetisation (Figure 3). These images can then be interleaved and a deconvolution operation performed to generate a high-resolution image.
This imaging experiment follows that of microSPAMM1,2,3, but with three important differences: i) the spatial modulation pattern has higher harmonic components; ii) the pattern is generated at the same time as phase encoding; and iii) the radiofrequency pulses have low power.
SNR Implications
By choosing acquisition conditions such that the width of the off-resonance peaks approximates that of the desired high-resolution voxel dimension ($$$Δx$$$), the SNR of the final 3D image ($$$SNR_{3DSR}$$$) can be expressed in terms of the SNR of the equivalent 3D spoiled gradient echo image acquired through traditional spatial encoding at a higher flip angle ($$$SNR_{3DGRE}$$$) as follows:$$SNR_{3DSR}\approx \frac{SNR_{3DGRE}}{\sqrt{\Delta x_{nom}/x}}$$
where $$$Δx_{nom}$$$ is the nominal voxel size of the low-resolution image. In comparison with traditional phase encoding, SNR efficiency is therefore reduced by approximately the square root of the resolution enhancement factor. However, the required RF power is dramatically reduced.
Methods
Phantom experiments were performed on a 9.4T Bruker BioSpec 94/20 equipped with a transmit-receive volume coil with an inner diameter of 40mm. A LEGO® brick was submerged in solution inside a cylindrical sample tube, and imaged at isocentre with the vendor’s 2D balanced SSFP sequence, modified to include an unbalanced spoiler gradient in the phase encode direction. The sequence parameters were as follows: TR/TE=5.0/2.5ms; NPE x NFE = 32x128; FOV = 58x40mm2; slice thickness = 1.2mm; α=0.4°; 1000 dummy TRs (5s of steady state preparation); 36 separate images at equidistant phase increments. This process provided a series of 36 low-resolution images with evenly spaced modulation patterns across the object. For clarity, these were simply interleaved with no deconvolution operation performed. A separate B0 map was acquired using the vendor’s standard sequence, with an isotropic resolution of 0.9mm.Results
The images are shown in Figures 4 and 5, with the super-resolution reconstruction demonstrating a clear improvement in the ability to visualise the phantom structure compared to the low-resolution acquired images. Despite the multi-shot nature of the acquisition, the image also shows homogeneous signal intensity across the object. However, there were clear distortion effects due to the combination of strong local B0 inhomogeneities (>200 Hz) and the very low input resolution (Figure 4).In regions where B0 was homogeneous, the simple super-resolution approach provided clear improvements in spatial resolution over the low-resolution input images, as well as when compared to a straightforward bicubic interpolation (Figure 5).
Conclusion
We have demonstrated that the off-resonance profile of the SSFP sequence can be exploited to achieve high degrees of super-resolution enhancement with minimal RF power requirements. This can be leveraged to reduce the TR as much as possible, opening up new opportunities for rapid high-resolution MRI, particularly in ultra-high magnetic fields.Acknowledgements
The authors wish to thank Dr Nicoleta Baxan for assisting with the phantom scanning, and Prof Brian Hargreaves for helpful discussions of the SNR implications of the technique. PJL is funded by the NIHR Imperial Biomedical Research Centre (BRC). PMM acknowledges generous funding from the UK Dementia Institute and is an NIHR Senior Investigator.References
- Ropele, S, Ebner, F, Fazekas, F and Reishofer, G (2010), Super‐resolution MRI using microscopic spatial modulation of magnetization. Magn. Reson. Med., 64: 1671-1675
- Hennel, F and Pruessmann, KP. (2017), MRI with phaseless encoding. Magn. Reson. Med., 78: 1029-1037
- Hennel, F, Tian, R, Engel, M, Pruessmann, KP. (2018) In‐plane “superresolution” MRI with phaseless sub‐pixel encoding. Magn. Reson. Med., 80: 2384– 2392
Figures
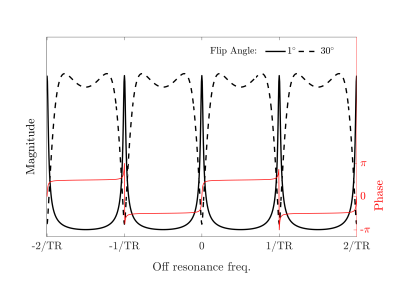
Figure 1:
Magnitude of the Bloch-simulated off-resonance profile for a
tissue with T1=600ms and T2=100ms, in a balanced steady state free precession
acquisition at flip angles of 1° (solid black line) and 30° (dashed black
line), with TR=5ms. The corresponding phase profile is overlaid in red.
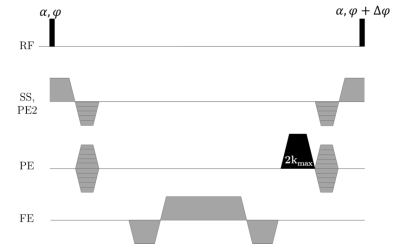
Figure 2: Sequence
diagram for the proposed technique, which uses an additional unbalanced spoiler
gradient (black) in one direction. Here the spoiler gradient is employed in the
phase encoding direction, but it can be applied along any axis.
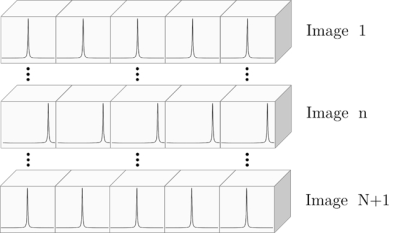
Figure 3: Schematic of the intravoxel signal
modulation during the experiment. Over a series of N images, the modulation
pattern is swept across the voxel in regular increments. These can then be
stitched together to create a super-resolution image.

Figure 4: Demonstration of the super-resolution
approach in the physical phantom. Left) The low-resolution input images had anisotropic
voxels, with a nominal resolution of 1.8x0.3mm2. Centre)
Super-resolution reconstruction effectively increased the apparent spatial
resolution. Right) This resolution enhancement succeeded even in the presence
of substantial static field inhomogeneities of (>200Hz).

Figure 5: Close-up of the images obtained from a
phantom, including (from left-right): a reference structural scout image; the
mean of the low-resolution input images; a bicubic interpolation of the mean of
the low-resolution input images; and the proposed super-resolution
reconstruction. The proposed approach clearly enhances spatial resolution in
comparison to straightforward image interpolation.