3722
Localized imaging using matrix gradient coils
Sebastian Littin1, Feng Jia1, Huijun Yu1, and Maxim Zaitsev1
1Department of Radiology, Medical Physics, University of Freiburg, University Medical Center, Freiburg, Germany
1Department of Radiology, Medical Physics, University of Freiburg, University Medical Center, Freiburg, Germany
Synopsis
Matrix gradient coils may be used for a non-linear phase preparation to suppress signals in unwanted regions. This allows for a reduction of the FOV smaller than the object without fold-over artifacts and can be seen as a viable alternative to selective excitation.
Introduction
MRI is rather slow compared to other imaging modalities. This is due to the fact that the data acquisition is performed consecutively. Each sample represents a specific harmonic component within the full image. Therefore, a reduction of the image size below the object size results in fold-over artifacts.We recently presented the design and implementation of a matrix gradient coil [1,2] which enables for a flexible generation of spatial encoding magnetic fields (SEMs). Nonetheless, due to Maxwell's equations a SEM cannot be shaped completely freely, e.g. to only produce linear encoding fields within a fraction of a slice and no field otherwise. One approach in lthe literature is to use multi-dimensional excitation, deploying timely excitation patterns. Alternatively, non-linear SEMs may be used to deliberately dephase MR signals outside the selected region [3]. Suppressed regions may then be neglected during the image encoding which may be used to speed up the acquisition or enhance the spatial resolution while keeping the same acquisition time.
Methods
Non-linear phase preparation has been presented by Witschey et al. [3]. In that work a quadratic SEM was used to shift signals out of the acquisition window. The formalism of local k-space has been used to to describe the induced signal shifts. The benefit of deploying quadratic SEMs is that a combination with linearly varying SEMs (constant gradients) enables to induce simple shifts of the area, where no signal scrambling is taking place throughout the FOV. Contrary to second order fields, the individual components of the matrix gradient coil we recently presented [1,2] are rather localized and do not represent spherical volume harmonics. In addition the element fields vary along all three spatial dimensions. Due to this additional variation along the through-slice direction, the local k-space formalism is not sufficient to describe all effects leading to the signal loss. In addition intra-voxel dephasing is crucial for a full understanding of the observed phenomena.A voxel based model to describe the signal behaviour in presence of non-linear SEMs was recently presented [4]. This model is based on the spatial extent of each voxel which is modeled as a boxcar-function. The corresponding Fourier transform is the sinc- function, which enables to described the intra-voxel signal behavior in presence of an non-linear SEM. The combination of signal shifts and intra-voxel dephasing effects enables a complete description of signal loss for arbitrary SEMs.
Phantom and in vivo measurements were performed on a 3T system, (Siemens Healthineers, Erlangen, Germany) equipped with 12 additional gradient power amplifier channels (GPAs) (IECO, Helsinki, Finland). The additional GPAs are controlled by custom interface hardware. Pulse sequences were programmed in the open source pulse sequence framework Pulseq [4,5]. Imaging experiments were performed with a gradient echo sequence with a prephasing time of 6ms and a readout time of 3.2ms. A slice thickness of 4mm, a flip angle of 25° and TE/TR of 10.6ms and 22ms were used.
A single chennel transmit/receive RF coil was used for phantom experiments. In addition an 8 channel receive coil was used in vivo. Images were acquired with a base resolution of 256.
The experienced volunteer gave his informed consent and the experiments were performed as self experiments.
Results
Phantom experiments demonstrating the signal signal suppression along one single direction are depicted in Figure 1. Suppression of MR signals outside the central stripe can be appreciated. The FOV was reduced along with the measurement time to 1/4 of the original size. As expected, a plain reduction of the FOV results in a fold-over artifact, whereas non-linear phase preparation results in an artifact-free image.The suppression pattern was rotated to demonstrate the flexibility with the matrix coil. Different orientations are depicted in Figure 2.
Figure 3 shows resulting in vivo images of the reduced field-of-view with and without suppression along with the original image for reference.
Discussion
The flexibility of matrix gradient coils may be used to deliberately spoil signals in unwanted regions. This may be used to reduce the number of the necessary phase encoding steps, which can directly be translated to the measurement time saving during the image encoding. However, the signal-to-noise ratio (SNR) is substantially reduced, since the SNR scales with the square root of the number of acquisition steps. This may be observed in the acquired examples. Therefore reduced FOV imaging is mostly advantageous for SNR-rich time-consuming acquisitions, such as high-resolution 3D imaging.One benefit of the method is that no additional time is needed during the acquisition since the phase preparation gradients are played out with the prephasing gradients. However, in the present experimental implementation the prephasing time had to be enlarged to allow for strong enough gradient amplitudes.
In theory non-linear phase preparation can be combined with parallel imaging techniques [6]. Yet, the effect of the additional phase on the signal has not been investigated yet in sufficient detail.
Acknowledgements
Deutsche Forschungsgemeinschaft (DFG) - Project number za422/5-1 and za422/6-1References
[1] F Jia, JMR
2017;281:217-228.
[2] S Littin, MRM 2018; 79:1181–1191.
[3] WR Witschey, MRM 2012; 67(6):1620-32.
[4] KJ Layton, MRM 2016;77:1544–1552.
[5] http://pulseq.github.io/
[6] M Zaitsev, MRM 2015; 73:1407–1419.Figures
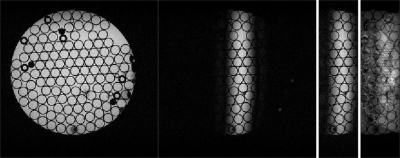
Figure 1: The full image is shown for reference a) (left). The application
of phase preparation gradients results in a signal suppression b)
(center left). A reduction of 3/4 of the original FOV becomes
possible without fold over artifacts c) (center right). The FOV was
reduced along the phase encoding direction. Therefore the measurement
time was effectively reduced by 3/4. A reduction of the FOV without
phase preparation results in severe fold-over artifacts c) (right).

Figure 2: Phantom Images of a pattern to suppress signals outside the
central image. This pattern is rotated to demonstrate the flexibility
of the matrix coil.
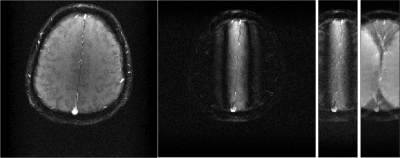
Figure 3: In vivo experiments similar to those shown in Fig.1. The full image is shown for reference a) (left). The application
of phase preparation gradients results in a signal suppression b)
(center left). A reduction of 3/4 of the original FOV becomes
possible without fold over artifacts c) (center right). The FOV was
reduced along the phase encoding direction. Therefore the measurement
time was effectively reduced by 3/4. A reduction of the FOV without
phase preparation results in severe fold-over artifacts c) (right).