Introduction

Acoustic noise during MR scans generated by the gradient coil vibration compromises patients’ comfort. Single-shot echo planar imaging (EPI), ubiquitously used in functional MRI and diffusion MRI acquisitions, has a rapid switching readout gradient, which is very efficient but also notoriously loud. Many attempts have been made toward a milder gradient waveform for EPI readout trajectory [1-3], which also benefit from the advances of fast imaging [2,3]. Meanwhile, careful choice of echo spacing according to the specific frequency response function (FRF) of a given scanner also helps noise reduction [4]. However the artificial design of sequence trajectory and parameter could not fully exploit the parameter space of k space filling to realize the full potential of noise reduction. In this study, we propose a framework to employ a model-free reinforcement learning agent to optimize pulse sequence parameters toward the “reward” of lower acoustic noise, under the constraint of appropriate k-space filling. Our preliminary results show that with the same scan time, the arbitrary trajectory produces acoustic noise 17.2 dB lower than EPI for a 2D single slice readout.

Methods

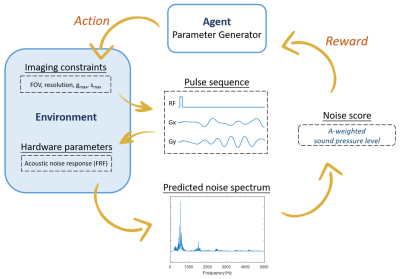
Reinforcement Learning Framework：
An AI agent takes “actions” to generate readout gradient waveforms under imaging constraints, after the slice selective RF pulse to encode the time-evolution of the imaging samples’ nuclear magnetization. The gradient waveform interacts with its “environment” defined by the frequency response function (FRF) of a given scanner. The environment then produces rewards based on acoustic noise estimation that guide the refinement of the agent’s actions (Figure 1). Our Bayesian approach to model this system is composed of pulse sequence actions A_i = [a_i(0), ..., a_i(N_T-1)] that are generated from a distribution p(A), in which i stands for the number of optimization iteration, and N_T represents the number of time points. In order to effectively capture the dynamic interplay between action A and their physical effect on acoustic noise level, we modeled p(A) using a dependent Gaussian process with sparseness-inducing priors. The predicted acoustic noise score y is obtained using the experimentally obtained FRF and generated action A. The updated model posterior p(f|y_i,A_i+1) proposes the next set of gradient waveform actions A* by maximizing an acquisition function u_i(A), which is chosen to be the expected improvement.
Experiments：
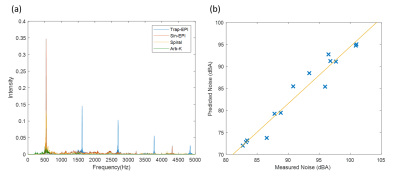
Experiments were performed on a 3T MR system (uMR790, United Imaging Healthcare, Shanghai). The sensor, an MR compatible condenser microphone (AWA 14423) was placed at the isocenter of the magnet bore. The frequency response function (FRF) of the scanner was obtained by applying the sweep-frequency sequence with gradient amplitude 3 mT/m and gradient switching frequency ramp from 20 Hz to 5000 Hz. Based on linear system assumption, the acoustic spectrum in the frequency domain S(f) can be estimated by S(f)=G(f) x H(f), where H(f) denotes the frequency response function, and G(f) for specific gradient waveform. And the predicted spectrum was then converted to the A-weighted sound pressure level SPA by an A-weighted filter. The acoustic noise score y was given by y= - SPA, as the guide for optimization. Single-shot EPI sequences with various bandwidth and imaging parameters were also applied to verify that the estimated acoustic noise accurately reflects actual noise.
Simulations:
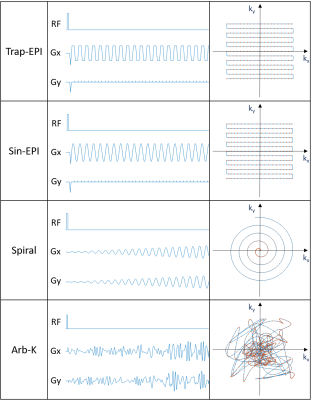
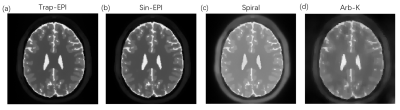
We employed the simulation platform bloch-simulator-python [5] for bloch simulation. The trapezoidal EPI (Trap-EPI), sinusoidal EPI (Sin-EPI), spiral and AI designed gradient waveforms (Arb-K) were each converted as input to the simulation module, other inputs of the simulation were 1) a 2D brain image imported from MRiLab [6] with matrix size= 200 × 200, resolution = 1 mm; with fixed T1 and T2 for each tissue compartments, 2) imaging parameters: FOV 20 x 20 cm², matrix size 128 x 128, flip angle = 90, TR = 400 ms; note that total readout time = 128 ms was fixed for different trajectories. Finally, image reconstruction was performed by solving the following optimization problem [7]: x = argmin Σ||FS_ix-d_i||₂ +λ||Dx||_1. Where F is the nonuniform fast Fourier transform (NUFFT) operator defined for specific sampling pattern [8], S_i is the ith coil sensitivity map (total of 16 coils), d_i is the corresponding ith k-space data, D is the sparse transform (i.e. total variation), λ is the regularization term. And image quality was evaluated by PSNR, MSE and image similarity (SSIM) as compared with input image.

Results and Discussion

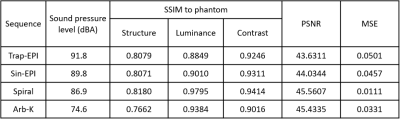
The schematic of gradient waveforms and their corresponding k-space trajectories are shown in Figure 2. As can be seen in Figure 3a, the acoustic frequency spectrum of the Arb-K has lower noise intensity as well as less high-frequency noise components. The acoustic noise estimated based on the measured scanner FRF is in very good agreement with the measured acoustic noise (Figure 3b). Table 1 summarizes the acoustic noise (dB) as well as the quality of the reconstructed images of all four sequences. The Arb-K trajectory reduces noise by 17.2 dB with slightly compromised image quality. Further work is needed to incorporate image quality into the reward loop of the reinforcement learning framework, which would likely better constrain the k-space filling pattern. To implement the sequence in realistic settings, potential challenges raised by gradient imperfections such as gradient delay, eddy current, as well as B₀ field inhomogeneities need to be considered.

Acknowledgements

This work is supported in part by grants 2017YFC0109002 and 18YF1410900.