Background

Three-dimensional radial trajectories provide an inherent isotropic resolution which facilitates multiplanar reformatting and simplifies planning. Numerous profile orderings have been proposed, one of which is the double golden-angle ordering (1). With the golden-angle profile order, a low number of readouts will provide an approximately uniform k-space coverage. As a corollary, an arbitrary subset of profile orderings will also result in an approximately uniform distribution. If the profiles are selected at random with equal probability, the corollary holds true. However, if the selection of profiles is based on a periodic function, such as heart rate from the electrocardiogram (ECG) of the subject, the k-space uniformity will degrade as spokes become clustered. Previous work (2,3) has described a solution to this problem in two-dimensional radial imaging where each heartbeat is acquired in a sector of the circular k-space, referred to as sector-wise golden angle (SWIG) profile ordering. In this study, we propose a three-dimensional sector-wise golden angle (3D-SWIG) profile ordering with preserved k-space uniformity after ECG-binning.

Methods

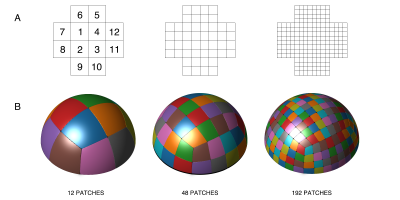
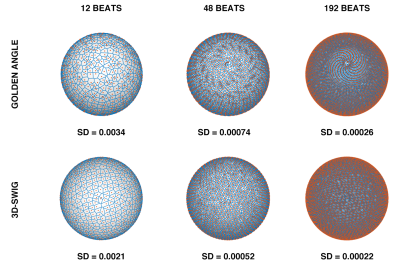
The double golden-angle method is based on two so-called golden means, $$$\phi_1 = 0.4656$$$ and $$$\phi_2 = 0.6823$$$. A uniform plane filling can be found by letting the x and y coordinates on the plane be defined by $$$\{m\phi_1\}$$$, $$$\{m\phi_2\}$$$ where m counts the readout number and $$$\{\}$$$ denotes the modulo of 1. Spherical coordinates $$$\alpha$$$ and $$$\beta$$$ are then found through an area-preserving transform from the plane to a hemisphere: $$\alpha = 2\pi\{m\phi_1\}, \beta = \cos^{-1}\left(\{m\phi_2\}\right).$$ To generalize the SWIG profile ordering method to three dimensions, a trivial approach would be to divide the plane into an arbitrary number of patches. However, while the mapping onto the sphere is area-preserving, it causes severe geometrical distortion of the patches, especially close to the poles. Instead, we propose tiling the surface as a half-cube, then utilizing a simultaneously low-distortion and area-preserving mapping from the half-cube to the hemisphere (4) given by $$X = x\cdot\sqrt{1-\frac{y^2}{2}-\frac{z^2}{2}-\frac{y^2z^2}{3}}, \quad Y = y\cdot\sqrt{1-\frac{z^2}{2}-\frac{x^2}{2}-\frac{z^2x^2}{3}}, \quad Z = z\cdot\sqrt{1-\frac{x^2}{2}-\frac{y^2}{2}-\frac{x^2y^2}{3}}$$ where lower-case variables correspond to coordinates on the cube and upper-case variables correspond to coordinates on the sphere. Profile orderings were calculated for N = 12, 48 and 192 patches, see Figure 1. A phantom was scanned at 3T (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany) using a prototype 3D-radial bSSFP pulse sequence which was modified with the proposed 3D-SWIG profile ordering. The sequence was triggered by a simulated ECG. Additionally, free-running double golden angle acquisitions were acquired with equal acquisition times. Relevant image parameters were; acquired isotropic voxel size: 1 mm³ isotropic, flip angle 50°, receiver bandwidth 1028 Hz/px, TE/TR: 1.7/3.4 ms. Binning simulations were performed with the simulated ECG. The k-space was sorted into 20 cardiac bins with a 140 ms reconstructed window width, which is comparable to previous studies (5). All images were reconstructed in MATLAB. The uniformity after binning was assessed through spherical Voronoi tessellation. The standard deviation of the Voronoi cell areas was used as a measure of sampling uniformity.

Results

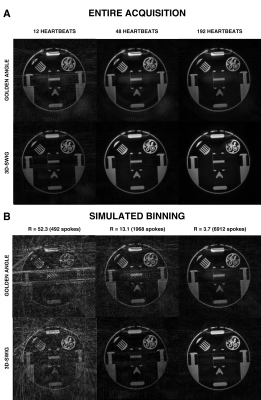
All reconstructions are presented in Figure 2. Qualitatively, 3D-SWIG showed fewer artifacts from undersampling (i.e. streaking). The k-space uniformity after physiological binning is presented as spherical Voronoi diagrams in Figure 3. Compared to golden-angle profile ordering, 3D-SWIG consistently had a lower standard deviation of the Voronoi cell areas, indicating superior sampling uniformity, and corroborating the qualitative results.

Conclusions

Conventional golden-angle imaging suffers from sampling heterogeneity after ECG binning. 3D-SWIG offers a simple solution that guarantees a uniform k-space distribution at all under-sampling factors. The bSSFP method is sensitive to eddy-current induced image artifacts. Thus, it is possible that some of the benefits of using 3D-SWIG can be attributed to the smaller angular steps between successive readouts, which is expected to result in lower amounts of eddy-current artifacts. The current study is only preliminary, and further work will show if the benefits of the 3D-SWIG method can translate to in-vivo imaging.

Acknowledgements

We acknowledge Siemens Healthcare (Erlangen, Germany) for access to the pulse sequence programming environment.