3713
Compressed sensing accelerated susceptibility-weighted imaging at 3T with SPARKLING: looking for favorable parametrization1CEA\DRF\JOLIOT\NeuroSpin\UNIRS, Gif-sur-Yvette, France, 2Siemens Healthcare SAS, Saint-Denis, France, 3CEA\DRF\JOLIOT\NeuroSpin\PARIETAL, Gif-sur-Yvette, France, 4AP-HP, Hôpital Henri Mondor, Service de Neuroradiologie, Paris, France
Synopsis
Compressed sensing (CS) theory has been successfully employed to drastically reduce MRI acquisition time. Recently, a new optimization-driven algorithm (SPARKLING) was proposed to design optimal non-Cartesian sampling patterns for CS-MRI. This method has several advantages compared to radial or spiral non-Cartesian imaging, yet the question on how the acceleration factor should be selected to ensure satisfactory image quality should be investigated. In this work, we applied the SPARKLING method for 3D susceptibility-weighted imaging, achieving 500μm in-plane resolution and full brain coverage in 3 minutes at 3T (6-fold acceleration compared to fully-sampled Cartesian imaging).
Introduction
Accelerating data acquisition while maintaining image quality in MRI has been a major interest in recent years. Using the Compressed sensing (CS) strategy1,2, data can be massively undersampled by a given acceleration factor compared to a fully-sampled Cartesian acquisition, while ensuring conditions for optimal image recovery. Recently, a new optimization-driven algorithm, called Spreading Projection Algorithm for Rapid K-space sampLING (SPARKLING3), was proposed to design optimal non-Cartesian sampling patterns for CS-MRI. Still, the question on how the maximum acceleration factor should be selected as a function of the acquisition matrix size and the available signal in order to maintain a desired image quality for SPARKLING, has been scarcely addressed4. In this work, we applied the stack-of-SPARKLING method for 3D susceptibility-weighted imaging (SWI) and investigated for a favorable parametrization on an MR phantom, ultimately achieving a full brain coverage in a clinically-compatible acquisition time (TA) on a healthy volunteer at 3T.Methods
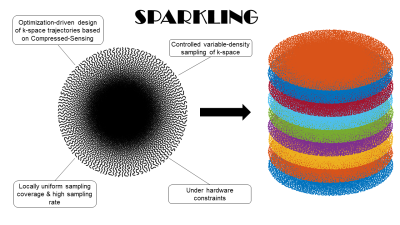
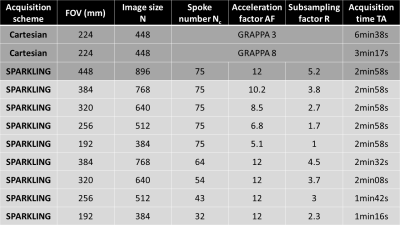
3D prospective acquisitions were performed at 3T (Siemens Healthineers Skyra & Prismafit, Erlangen, Germany) using 64-ch head coils and a 3D GRE sequence compatible with arbitrary gradients on one healthy volunteer (male, 45 yo) and on an MR phantom (NIST, Gaithersburg, MD, USA). The nominal gradient amplitude and slew rate were 40 mT/m and 180 T/m/s, respectively. SWI acquisition parameters were set as follows: TR=37ms, TE=20ms, FA=15°, Tobs=20ms, partition number Nz=64. An example of 2D SPARKLING trajectory is illustrated in Figure 1. In the search of favorable SPARKLING parametrization on MR phantom, multiple acceleration factors (AF), subsampling factors (R) and matrix sizes were used, while keeping the same spatial resolution (note: only in-plane acceleration was investigated). Parameters for Cartesian and SPARKLING acquisitions are provided in Figure 2. Non-Cartesian data were reconstructed by minimizing a classical CS multichannel regularized criterion balancing the trade-off between data consistency and L1-based sparsity in the wavelet domain5. Structural similarity metrics (SSIM) were computed between SPARKLING images and the Cartesian reference to quantify image quality. SWI phase processing6 was achieved using a high-pass customized Hanning filter and Homodyne detection.Results
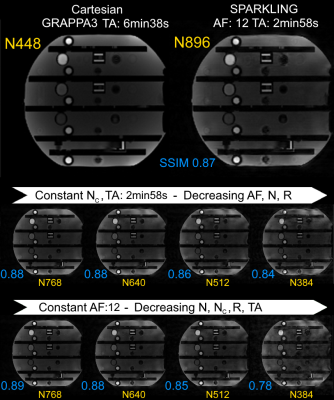
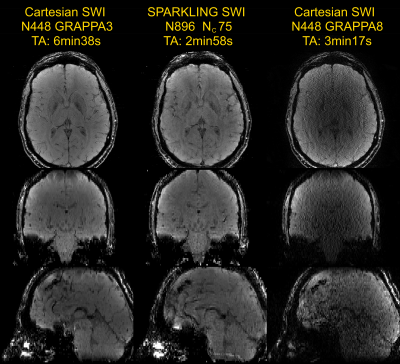
Figure 3 illustrates SPARKLING acquisition results on phantom. SSIM scores showed increased SPARKLING image fidelity when larger matrix sizes are used while: 1/ keeping the TA constant (central row), and 2/ keeping the AF constant (bottom row). Cartesian and SPARKLING in vivo SWI images are compared in Figure 4. Reference Cartesian acquisition with GRAPPA3 parallel imaging exhibited very high image quality for a TA>6 min. The SPARKLING acquisition, even with a larger matrix size, was twice as fast and successfully maintained image quality, with overall similar image contrast and slightly degraded spatial resolution. The depiction of venous contribution in SWI signal is clearly possible in SPARKLING images. Off-resonance artifacts requiring additional corrections7 are also visible. The Cartesian acquisition with a comparable TA (in-plane GRAPPA8) showed extremely poor image quality.Discussion
SWI requires relatively long TE and Tobs and could therefore benefit from SPARKLING to drastically reduce TA, or to reach spatial resolution commonly achieved at ultra-high field using a clinical setup. Phantom acquisitions with matrix sizes significantly larger than the object outperform acquisitions with smaller matrices, presumably revealing an optimal regime for the SPARKLING method. However, the gain in TA of SPARKLING acquisitions using matrix sizes twice as large as Cartesian reference is ultimately halved. Nevertheless, SPARKLING achieved better relative performances than conventional parallel imaging techniques (in-plane GRAPPA8) both in terms of image quality and TA reduction. In the future, undersampling along the third dimension, or full 3D SPARKLING patterns, could contribute to further TA reduction9. Objective comparisons with spiral10, segmented-EPI11, and CAIPIRINHA12 imaging are still required to assess this promising technique.Conclusion
Overall, these preliminary results showed a favorable operating regime for SPARKLING when large matrix sizes are used. Using such parametrization, 500µm in-plane resolution SWI was successfully achieved in only 3 minutes at 3T using stack-of-SPARKLING. Ongoing work toward retrospective reconstruction of undersampled data using various SPARKLING trajectories should contribute to uncover this optimal regime.Acknowledgements
This project has received financial support from the CEA DRF ‘Invention’ funding program through the ‘MANIAC’ project.References
1Lustig et al. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 58:1182-1195 (2007).
2Lustig et al. Compressed sensing MRI. IEEE Signal Process Mag 25:72-82 (2008).
3Lazarus et al. SPARKLING: variable-density k-space filling curves for accelerated T2*-weighted MRI. Magn Reson Med 81:3643-3661 (2019).
4Lazarus et al. An empirical study of the maximum degree of undersampling in compressed sensing for T2*-weighted MRI. Magn Reson Imaging 53:112-122 (2018).
5El Gueddari et al. Self-calibrating nonlinear reconstruction algorithms for variable density sampling and parallel reception MRI. 10th IEEE Sensor Array and Multichannel Signal Processing workshop (2018).
6Haacke et al. Susceptibility weighted imaging (SWI). Magn Reson Med 52:612-618 (2004).
7Man et al. Multifrequency Interpolation for Fast Off-resonance Correction. Magn Reson Med 37:785-792 (1997).
8Griswold et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 47:1202-1210 (2002).
9Lazarus et al. 3D SPARKLING for accelerated ex vivo T2*-weighted MRI with compressed sensing. ISMRM 2019 p4573.
10Lee et al. Fast 3D imaging using variable‐density spiral trajectories with applications to limb perfusion. Magn Reson Med 50:1276-1285 (2003).
11Sati P. Diagnosis of multiple sclerosis through the lens of ultra-high-field MRI. J Magn Reson. 291:101-109 (2018).
12Breuer et al. Controlled Aliasing in Parallel Imaging Results in Higher Acceleration (CAIPIRINHA) for Multi-Slice Imaging. Magn Reson Med 53:684-691 (2005).
Figures