3699
Universal Parallel Transmit Pulse Design for 3-D Local-Excitation based on different sized databases of B0/B1+-maps – A 7T Study
Ole Geldschläger1, Tingting Shao1, Jürgen Herrler2, Armin Nagel3,4, and Anke Henning1,5
1High-field Magnetic Resonance, Max-Planck-Institut for biolog. Cybernetics, Tübingen, Germany, 2Institute of Neuroradiology, University Hospital Erlangen, Erlangen, Germany, 3Institute of Radiology, University Hospital Erlangen, Erlangen, Germany, 4Institute of Medical Physics, Friedrich Alexander University Erlangen Nürnberg, Erlangen, Germany, 5Advanced Imaging Research Center, University of Texas Southwestern Medical Center, Dallas, TX, United States
1High-field Magnetic Resonance, Max-Planck-Institut for biolog. Cybernetics, Tübingen, Germany, 2Institute of Neuroradiology, University Hospital Erlangen, Erlangen, Germany, 3Institute of Radiology, University Hospital Erlangen, Erlangen, Germany, 4Institute of Medical Physics, Friedrich Alexander University Erlangen Nürnberg, Erlangen, Germany, 5Advanced Imaging Research Center, University of Texas Southwestern Medical Center, Dallas, TX, United States
Synopsis
This study investigates universal parallel-transmission (pTx) radio-frequency-pulses for 3-dimensional local-excitation designed on different sized databases of B0/B1+-maps from human heads at 7T. Thus, it prospectively abandons the need for time-consuming subject specific B0/B1+-mapping and pTx-pulse calculation during the scan session. For the proposed calculation routine, the design-database does not need to include more than five heads, to achieve a pTx-pulse that excites the same 3-dimensional local-excitation target-pattern on the tested 40 different heads. The resulting universal pulses created magnetization-profiles with (in most cases) an only marginally worse Normalized-Root-Mean-Square-Error compared to the magnetization-profiles produced by pulses tailored to individual heads.
Introduction
Parallel-transmission (pTx) radio-frequency (RF) systems offer additional degrees of freedom for designing tailored RF-pulses (TPs). However, pTx-pulse-design often includes measuring the B0 and channel-wise B1+field distribution for each subject. In addition, the pulse calculation is currently performed during the scan-session. This procedure leads to lengthy scan times and prevents clinical and research-applications of pTx.Gras et al.1,2,3 introduced the concept of ‘universal’ pTx-pulses (UPs), which does not require the knowledge of B0-variations and channel-wise B1+ distribution in individual subjects, and rather relies on a pre-calculated pulse database. However, these studies only considered the case of homogenous whole-brain excitation pulses. In own previous studies4,5, we extend the UP concept to 2- and 3-dimensional local excitation, based on a relative small database of B0/B1+-maps. In this work, we investigate UPs for 3-dimensional (3D) local-excitation-pulses optimized on different sized (one to eight included heads) databases of B0/B1+-maps. Furthermore, the calculated UPs will be tested on 32 B0/B1+-maps that were not included in the design-database.
Methods
For 40 different heads of healthy volunteers the B0- and the B1+-maps from each transmit channel of an 8-channel RF-coil were measured using a 7T whole body MRI scanner (Siemens Terra).Eight different sized databases of B0/B1+-maps were created, based on which the UPs were calculated. The first tested database contained the B0/B1+-map from ‘head one’ (DB1), the second database contained two B0/B1+-maps; from ‘head one’ and from ‘head two’ (DB2), etc. The eighth database contained the eight B0/B1+-maps from ‘head one’ to ‘head eight’ (DB8). In advance, all maps were sorted randomly.
The goal was to design single UPs that would consistently excite the same 3D local pattern with a desired flip angle (FA) on all heads that are in the database, respectively. The UP designed based on DB1 is referred to UP-DB1; the UP designed based on DB2 is referred to UP-DB2; etc.
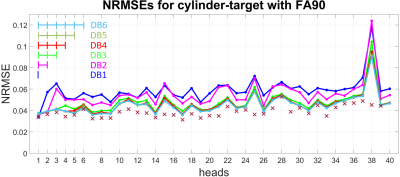
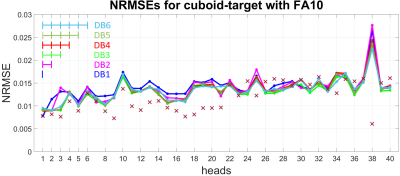
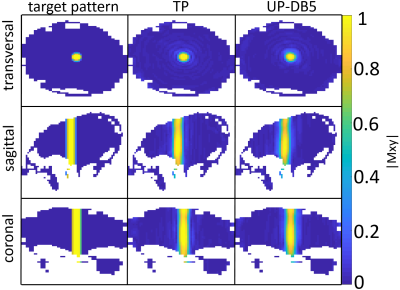
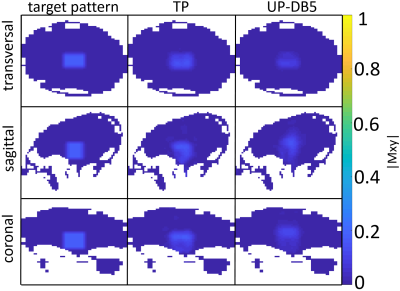
Two 3D-local-excitation test-target-patterns where chosen: A cylinder reaching from the top to the bottom of each head with a target FA of 90° (FA90) (see left column in Figure 3) and a cuboid in the center of each head with a target FA of 10° (FA10) (see left column in Figure 4).
After calculation, the UPs were applied on all of the 40 heads, respectively. The performances of the UPs were compared with the performances of the TPs by calculating the Normalized-Root-Mean-Square-Error (NRMSE) between the resulting magnetization profiles and the target-patterns.
To calculate the UPs, the method from Geldschläger et al.5 was used. The idea of this approach is basically to extend the spatial domain method6 to include more than one subject for which the pulse will be optimized.
To calculate the TPs, the spatial information from only the corresponding subject will be used as the design-database.
3D-stack-spiral-in k-space-trajectories and a pulse-duration of 2.21ms (8.02ms) for the cylinder (cuboid), were chosen. T1- and T2-relaxation times were not considered during this 7T simulation-study.
Results
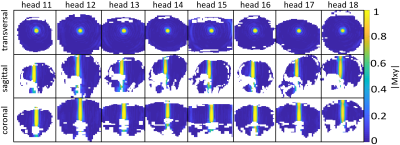
As depicted in Figure 1 and Figure 2, the NRMEs of the UPs decrease with increasing number of heads in the design-database for both target-patterns. For database sizes ≥5 the performances of the UPs are almost identical on each head. For the sake of clarity, the results from the UP-DB7 and UP-DB8 are not shown. They differ negligibly from the results of UP-DB5 and UP-DB6. Except of some heads for the cuboid-target pattern, the TPs outperform every UP. The different scales of the y-axis in Figure 1 and Figure 2 is worth noting.In Figure 3 and Figure 4, the magnetization-profiles after application of the TPs and UP-DB5 for both targets, respectively, are highly similar. The same is valid for the results in Figure 5, where UP-DB5 creates similar profiles on eight example heads, which were not in the design-database included.
Discussion
Except of on head 38, the UPs with a database size ≥5 perform almost identical on each head, respectively. Possibly, head 38 exhibits anatomical abnormalities or measurement errors occur during the B0/B1+-map acquisition.Due to the lower target FA10 for the cuboid target-pattern compared to the FA90 for the cylinder target-pattern, the excitation (non-excitation) of a voxel that is not excited (excited) in the target has not that strong influence on the NRMSE. That results in lower NRMSEs for the cuboid target-pattern as for the cylinder target-pattern. However, for both targets, the performances of UPs with database size ≥5 are excellent, as they perform marginal worse compared to the TPs. That is valid for heads that were in the design-database included, as well as on heads that were not included.
Conclusion
With the proposed UP-design routine, not more than five database heads are necessary to create reliably pulses that achieve the same 3D-local-excitation pattern with a desired FA across a large cohort of subject heads. As this is especially true for heads that were not the database inherent, the time-consuming per subject B0/B1+-map-measurements can potentially be eliminated from the pTx-scan-sessions in future. This significantly reduces the scan time, abandons the need of subject specific pulse optimization while the subject is waiting in the scanner and might open up new possibilities in the field of pTx-pulse-design methods.Acknowledgements
Funding by the European Union (ERC Starting Grant, SYNAPLAST MR, Grant Number: 679927) is gratefully acknowledged.References
1. Gras V, Vignaud A, Amadon A, Bihan DL, Boulant N. Universal pulses: A new concept for calibration-free parallel transmission. Magnetic Resonance in Medicine. 2016 Feb; 77: 635-643.
2. Gras V, Mauconduit F, Vignaud A, Amadon A, Bihan DL, Stöcker T, et al. Design of universal parallel-transmit refocusing kT -point pulses and application to 3D T2 -weighted imaging at 7T. Magnetic Resonance in Medicine. 2017 Nov; 80: 53-65.
3. Gras V, Pracht ED, Mauconduit F, Bihan DL, Stöcker T, Boulant N. Robust nonadiabatic T2 preparation using universal parallel-transmit kT -point pulses for 3D FLAIR imaging at 7 T. Magnetic Resonance in Medicine. 2019 Jan; 81: 3202-3208.
4. Geldschläger O, Shao T, Henning A. Universal Parallel Transmit Pulse Design for Local Excitation. In Proceedings of Joint Annual Meeting ISMRM-ESMRMB 2018, Paris, France.; 2018.
5. Geldschläger O, Shao T, Henning A. Universal Parallel Transmit Pulse Design for 3-Dimensional Local-Excitation – A 9.4T Simulation Study. In Proceedings of Annual Meeting 27th ISMRM, Montreal, Canada; 2019.
6. Grissom W, Yip Cy, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magnetic Resonance in Medicine. 2006; 56: 620-629.
Figures
Figure 1: Comparison of the Normalized Root
Mean Square Errors (NRMSEs) between the resulting magnetization profiles and
the cylinder-target pattern with FA90. Each line corresponds to one UP, applied
on each of the 40 heads. The blue line marks the NRMSEs resulting for the
application of UP-DB1; the pink line marks the NRMSEs for the application of
UP-DB2; etc. The dark-red crosses mark the NRMSE of the TPs for each head. The
legend in the top left corner depicts which heads belong to which database.
Figure 2: Comparison of the Normalized Root
Mean Square Errors (NRMSEs) between the resulting magnetization profiles and
the cuboid-target pattern with FA10. Each line corresponds to one UP, applied
on each of the 40 heads. The blue line marks the NRMSEs resulting for the
application of UP-DB1; the pink line marks the NRMSEs for the application of
UP-DB2; etc. The dark-red crosses mark the NRMSE of the TPs for each head. The
legend in the top left corner depicts which heads belong to which database.
Figure 3: Cylinder-target-pattern with FA90
and 3D-magnetization profiles (for head 20, not in the design-database) created
by TP and UP-DB5. Depicted in the rows is the central slice for each view. In the first column, the target-pattern is visible. The second
column shows the magnetization profile created by the TP. The third column
presents the UP-DB5 performance. Since the target FA is 90°, |Mxy| ≈ sin(90°) = 1
in
the excited areas in the TP- and UP-profiles. In some areas where no excitation
should be at all, there is very low excitation in both profiles. Both profiles
look very similar.
Figure 4: Cuboid-target-pattern with FA10 and
3D-magnetization profiles (for head 5, not in the design-database) created by TP and the UP-DB5. Depicted in the rows is the central slice for each view. In the first column, the target-pattern is visible. The second
column shows the magnetization profile created by the TP. The third column
presents the UP-DB5 performance. Since the target FA is 10°,
|Mxy| ≈ sin(10°) = 0.17 in
the excited areas in the TP- and UP-profiles. In the areas where
no excitation should be at all, there is almost no signal in
both profiles. Both profiles look very similar.
Figure 5: Magnetization profiles of head 11 to
head 18 after application of the UP-DB5, for cylinder-target pattern with FA90.
Depicted in the rows is the central slice for each perspective. Each
column represents one head.