3692

Designing B₀ robust adiabatic multi-band inversion pulses with high time-bandwidth products and smooth slice selective gradients

Christoph Stefan Aigner¹ and Sebastian Schmitter¹
¹Physikalisch-Technische Bundesanstalt (PTB), Braunschweig and Berlin, Germany

Synopsis

We demonstrate the design of adiabatic multi-band inversion pulses with high time-bandwidth products and acceptable RF power demands. The proposed utilization of GOIA single-band pulses results in smooth slice selective gradients with highly reduced RF power and matched multi-band RF waveforms. Phantom and in vivo experiments at 3T and 7T validate the simulations and demonstrate robust inversion of multiple slices over a wide range of both B₁⁺ and B₀values.

Target audience:

Researchers interested in the field of RF pulse design, SMS imaging and spectroscopy.

Purpose:

Ultra-high field MR is often limited by inhomogeneities of the transmit magnetic radio frequency (RF) field (B₁⁺) yielding spatially variable flip angles (FA). Adiabatic RF pulses generate homogeneous FA despite B₁⁺ variations while achieving high spectral or spatial selectivity¹. Different approaches have been proposed to increase the bandwidth of adiabatic single-band (SB) pulses by reducing RF peak amplitudes² or a combined reduction of RF peak amplitudes and RF power^3,4. In this work, we extend adiabatic multi-band (MB) pulses⁵ where RF power becomes an even stronger problem and propose to use low-power gradient-offset independent adiabatic (GOIA⁴) pulses with the aim to design adiabatic MB pulses with high bandwidth, smooth slice-selective gradient (G_s) shape and increased B₀ robustness. The proposed pulses were tested on numerical simulations and validated experimentally at 3T and 7T.

Theory:

A frequency offset shifts adiabatic pulses along the spectral or spatial dimension. As for conventional MB pulses⁶, a spatially selective adiabatic MB pulse is achieved by superposing $$$N$$$ adiabatic SB pulses $$$B_1(t)$$$, each shifted with respect to isocenter to a different spatial position $$$\Delta\,z_n$$$ using $$B_{1,MB}(t)=\sum_{n=1}^{N}B_1(t)e^{i(k(t)\Delta\,z_n+\theta_n)}.$$ Instead of a constant frequency offset we use the more general spatial frequency variable $$$k(t)=-\gamma\int_{0}^{t}G_s(t)\,dt$$$ and $$$\theta_n$$$ for phase scrambling^6,7,8. This allows designing MB pulses with arbitrary G_s shapes and can be directly applied to the GOIA waveforms based on n-th-order hyperbolic secant (HS) functions. The GOIA RF phase modulation $$\phi(t)= \frac{2\pi}{Q}\int_{0}^{t}(G_{s}(\tau)\int_{0}^{\tau}\frac{ B_{1}(\tau^´)^2}{G_{s}(\tau^´)}d\tau^´-\omega_c)d\tau,$$ with center frequency $$$\omega_c$$$ was computed for each SB pulse based on numerical integration of the constant adiabatic equation⁴ with a constant quality factor $$$Q$$$.

Methods:

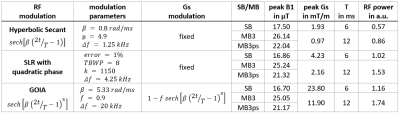
Three different adiabatic inversion pulses, HS¹, Shinnar–Le Roux with quadratic phase (SLR)² and GOIA^4,5 were designed in MATLAB (The MathWorks, Inc, Natick, USA) according to Figure 1. The pulses were designed for a duration of 6 ms/12 ms (SB/MB) and temporal discretization of 5 µs to leave room for B₁ scaling above the adiabatic threshold. The spectral bandwidth of the pulses ranged from 1.25 kHz (HS) to 4.25 kHz (SLR) and 20 kHz (GOIA). Gradients were designed for a slice thickness of 20 mm and temporal discretization of 10 µs. Three SB pulses, inverting at isocenter or ±50 mm away, were superposed to form an MB pulse without (MB3) and with an optimized phase scrambling scheme (MB3ps)⁷. The total power of the RF pulse was estimated by $$$\int_{0}^{T}B_1(t)^2\,dt$$$. The MB3ps inversion pulses were implemented in a pulse sequence followed by an orthogonal slice selective excitation and cartesian phase encoding and read-out. High-resolution scans (TR/TE = 2000/4.8 ms, FOV = 256x128 mm, matrix = 384×192, B1 up to 150%) have been acquired on a 3T system (Magnetom Verio, Siemens, Erlangen, Germany) with a 32Rx head coil and on a 7T system (Magnetom, Siemens, Erlangen, Germany) with a 1Tx32Rx head coil. Each scan was performed twice (without and with the adiabatic inversion pulse) and the inversion profiles were calculated by the difference between the two resulting images.

Results and Discussion:

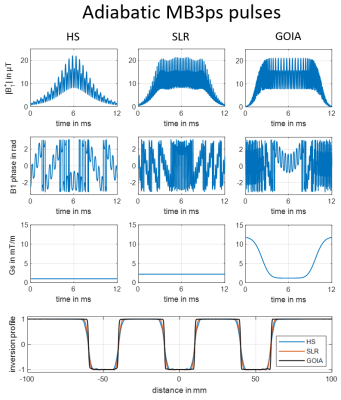
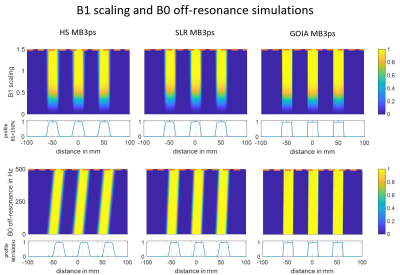
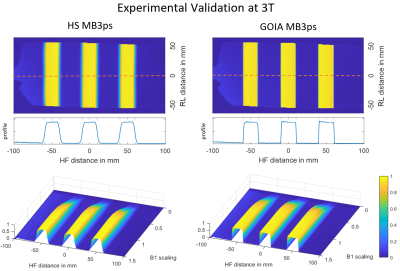
Figure 1 lists key parameters for all pulses. It bears mentioning that the GOIA pulse has similar RF power demands as the SLR pulse but has a more than 5 times higher bandwidth. A similar performance might be possible by applying VERSE, but GOIA additionally achieves a constant adiabatic factor across the entire spectral bandwidth⁴. Compared to HS-MB3ps the proposed GOIA-MB3ps pulse results in a 16 times higher bandwidth with only a 2-fold RF power increase. As expected, phase scrambling of adiabatic MB pulses resulted in a sub-linear scaling of the peak B₁⁺ amplitude and linear scaling of RF power demands with the number of bands. Figure 2 shows the MB3ps waveforms and the simulated inversion profiles. The simulations demonstrate the feasibility of simultaneous triple-slice inversion. While all RF magnitudes and phases vary rapidly, the G_s waveform (for GOIA) is smooth and does not require correction of gradient imperfections^8,9. Figure 3 shows simulated inversion profiles (scaled from 0 to 1) of the Mb3ps pulses for a B₁⁺ variation of 0-150% and off-resonance frequencies from 0-500 Hz. The pulses perform similar near the adiabatic (B₁) threshold but differ in off-resonance sensitivity. A 500 Hz B₀ offset shifts the inversion profiles by 12 mm (HS), 5.4 mm (SLR) and only 1.2 mm (GOIA). Notably, the GOIA-MB3ps pulse achieves inversion profiles with a maximal error of only 2.5% at 500 Hz, despite the time-varying gradient. Figure 4 shows the reconstructed inversion profiles for HS- and GOIA-MB3ps from 3T phantom measurements. B₁ was varied up to 150% in eleven steps and the results reproduce the Bloch simulations shown in Figures 2 and 3. Figure 5 shows phantom and in-vivo inversion profiles measured at 7T together with GRE reference scans and B₀ maps. Again, the measurements agree well with the simulations and clearly demonstrate the robustness and practical applicability of the GOIA-MB3ps pulses.

Conclusion

Bloch simulations and measurements at 3T and 7T consistently confirm the hypothesized potential of phase-scrambled adiabatic GOIA-MB pulses. These pulses will serve as a basis to reduce effective echo time and chemical shift artifacts in multi-voxel spectroscopy.

Acknowledgements

No acknowledgement found.

References

1) Tannus A, Garwood M. Adiabatic pulses. NMR Biomed 1997; 10: 423–434.

2) Balchandani P, Pauly J and Spielman D, Designing adiabatic radio frequency pulses using the Shinnar–Le Roux algorithm. Magn. Reson. Med., 64: 843-851, 2010 doi:10.1002/mrm.22473

3) Warnking JM and Pike GB, Bandwidth‐modulated adiabatic RF pulses for uniform selective saturation and inversion. Magn. Reson. Med., 52: 1190-1199, 2004 doi:10.1002/mrm.20262

4) Andronesi OC, Ramadan S, Ratai EM, Jennings D, Mountford CE and Sorensen AG, Spectroscopic imaging with improved gradient modulated constant adiabaticity pulses on high-field clinical scanners. J. Magn. Reson., 203(2): 283-293, 2010. doi: 10.1016/j.jmr.2010.01.010.

5) Goelman G and Leigh JS, Multiband Adiabatic Inversion Pulses. J. Magn. Reson. 101(2): 136-146, 1993. doi: 10.1006/jmra.1993.1023.

6) Barth M, Breuer F, Koopmans PJ, Norris DG and Poser BA. Simultaneous multislice (SMS) imaging techniques. Magn. Reson. Med. 75(1):63–81, 2016.

7) Wong EC, Optimized phase schedules for minimizing peak RFpower in simultaneous multi-slice RF excitation pulses. Proc.Intl.Soc.Mag.Reson.Med. 2012;(20):2209

8) S. Abo Seada, A.N. Price, T. Schneider, J.V. Hajnal, S.J. Malik, Multiband RF pulse design for realistic gradient performance. Magn Reson Med. 2019; 81: 362– 376. https://doi.org/10.1002/mrm.27411

9) C.S. Aigner, A. Rund, S. Abo Seada, S. Malik, J.V. Hajnal, K. Kunisch and R. Stollberger. Time-optimal control based RF pulse design under gradient imperfections. Magn. Reson. Med. 2019; 00: 1– 14. https://doi.org/10.1002/mrm.27955

Figures

Figure 1: Design parameters and performance of the adiabatic Hyperbolic Secant (HS), Shinnar-Le Roux (SLR) and GOIA adiabatic inversion pulses, each as single-band (SB) or triple-band (MB3) pulse with and without phase scrambling (ps). For GOIA, also the slice selective gradient (G_s) shape is given. Columns 1-3 give the design parameters and achieved bandwidth Δf. Columns 5-8 summarize the respective pulse performance in terms of required peak B₁ amplitude, peak G_s amplitude and RF power. The pulse duration of the MB pulses was intentionally set to 12 ms to leave room for B₁ scaling.

Figure 2: RF magnitude, RF phase and slice selective gradient (G_s) shapes for simultaneous adiabatic inversion of 3 slices (20 mm thickness and +/-50 mm slice offset). Row 4 shows the simulated inversion profile 1-|2b(z)| for each spatial position z in the spin domain. Note that the higher bandwidth of the proposed GOIA MB3ps pulse is realized with similar RF power as the SLR example by utilizing a time-varying G_s waveform with very modest demands on the gradient system.

Figure 3: Simulated inversion profiles for each spatial position z in the spin domain (scaled from 0 to 1) to predict performance the adiabatic HS, SLR and GOIA MB3ps examples from Figure 2 in the presence of B₁ and B₀ inhomogeneities. The simulations in the first row are performed assuming an ideal B₀ field with a B₀ off-resonance of 0 Hz. The simulations in the second row are performed with a fixed B₁ scaling of 1.5. Compared to the other MB3 pulses, the GOIA MB3ps achieves the best slice profiles and off-resonance performance.

Figure 4: Inversion slice profile measurements in a phantom bottle using the adiabatic HS- and GOIA-MB3ps pulses shown in Figure 2 on a 3T system. The inversion slices are computed from two measurements without and with the inversion pulse and have been normalized with a reference scan. The noise level change results from spatially varying SNR in head-feet (HF) direction. The cross-section indicates an excellent match to the simulations in Figure 2. The last row shows the same cross-section of 11 measurements with different B₁ scaling that reproduce the simulations shown in Figure 3.

Figure 5: Inversion slice profile measurements in a phantom bottle and a healthy volunteer using the adiabatic HS- and GOIA-MB3ps pulses from Figure 2 at a 7T system. The reconstructed inversion slices were computed from two measurements without and with the inversion pulse and have been normalized by a reference scan. The reconstructed data clearly shows a precise inversion of the proposed GOIA MB3ps example despite B₁⁺ and B₀ variations.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3692