3683

Radial sampling interactions in multi-dimensional sparse encoding problems using a joint decoding-reconstruction framework

Sophie Schauman¹, Thomas W Okell¹, and Mark Chiew¹
¹Wellcome Centre for Integrative Neuroimaging, NDCN, University of Oxford, Oxford, United Kingdom

Synopsis

Many physical properties cannot be directly measured with MRI, but are instead derived from a number of encoded measurements. Novel sampling methods in these regimes generally consider how to sample these encoded signals in k or k-t space, but not how to best sample across encodings. Here we present a study into how choice of encoding protocol interacts with the sampling and how these choices affect the multi-dimesnional point spread function. Simulations on vessel-encoded ASL angiography are used to study how these choices affect image reconstruction quality. We show that jointly decoding and reconstructing improves image reconstruction fidelity.

Introduction

Many MR measures are indirectly inferred from multiple measurements or encodings. However, methods often consider sampling in k or k-t space separately from sampling across different encoded measurements. Additionally, image reconstruction and decoding of the signal of interest are often treated separately, rather than inferring the signal of interest directly from the measured data. We propose that by considering the signal encoding and image acquisition jointly, the properties of the measurement operators, characterized by the multi-dimensional point spread function (m-PSF)¹, can be modulated for improved reconstruction fidelity.
We present a proof-of-principle evaluation of encoding and sampling strategies for a vessel-encoded arterial spin labeling (VE-ASL) angiography acquisition that is decoded and reconstructed using sparsity constraints². We further consider modification of the encoding operator when the different signal components carry different amounts of energy: in the case of VE-ASL angiography, the signal intensity of the static tissue is much larger than that of the vessel components.

Theory

The acquisition operator, $$$\mathbf{E}$$$, for ASL angiography can be modeled in three parts, $$$\mathbf{E}=\mathbf{FSH}$$$. The vessel encoding operator, $$$\mathbf{H}$$$, describes how the blood signal arising from each proximal artery has been modulated for each acquired dataset; the coil sensitivities, $$$\mathbf{S}$$$, spatially modulate the signal received by each receive coil; and the Fourier transform, $$$\mathbf{F}$$$ models sampling based on the imaging trajectory.
For a sparsity constrained reconstruction, incoherence of the acquisition operator is important³. By changing $$$\mathbf{F}$$$ (trajectory) and $$$\mathbf{H}$$$ (encoding scheme), we can modulate the spreading of aliased signal across both space and vessel components. We exclude $$$\mathbf{S}$$$ from this analysis, because it can only be modified by hardware design.
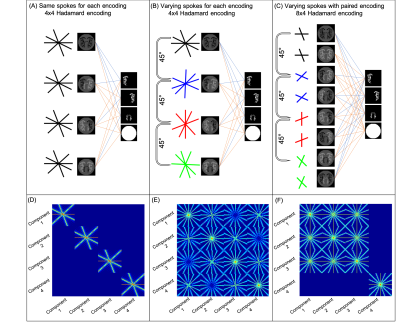
The m-PSF characterize both within-component spatial aliasing distributions, and between-component aliasing, and is defined by examining every pair-wise PSF $$$(\mathbf{E}’\mathbf{Eu}_i)_j$$$, where $$$\mathbf{u}_{i}$$$ is a vector of zeros except one entry of 1 in the i^thcomponent, and the index j denotes the PSF in the j^thcomponent. Then the m-PSF can be expressed as a symmetric matrix where the m-PSF_ij represents the aliasing of energy from the i^thcomponent into the j^thcomponent.

Methods

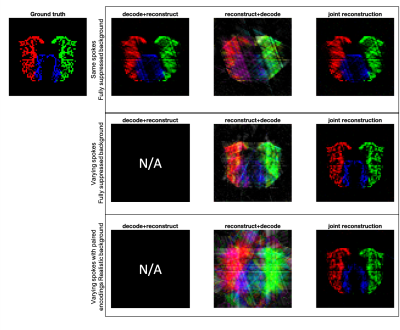
To examine the properties of the joint reconstruction scheme, we simulated 4-component 64x64 ASL angiography images, reconstructed in three ways:

‘decode+reconstruct’: Decode first then reconstruct – this can only be done when each encoding has the same k-space sampling
‘reconstruct+decode’: Reconstruct encoded images, then decode – can be done with any sampling scheme
‘joint-reconstruction’: Jointly reconstruct and decode – sampling and encoding operators interact.

For reconstruction we used a simple basis pursuit denoising model with sparsity enforced in decoded image space as angiograms are spatially sparse. The simulations were based on variations of 2D golden angle radial trajectories using 16 spokes (spread across encodings). R = 25.3 compared with 4 fully sampled encodings. Three different acquisition and encoding methods were used (Figure 1):

Golden angle sampling with fixed sampling across encodings with a 4x4 Hadamard encoding (4 spokes per encoding)
Golden angle with uniform radial increments across encodings with a 4x4 Hadamard encoding (4 spokes per encoding)
Golden angle with uniform radial increments across every other encoding for static tissue removal with a paired 8x4 Hadamard encoding (2 spokes per encoding)

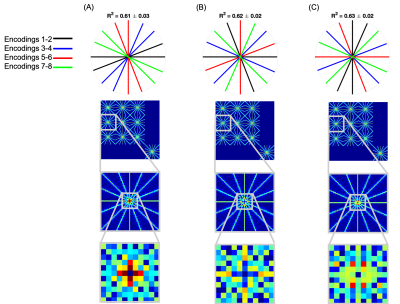
Each reconstruction was performed on 10 augmentations of ground truth data, each with 10 instances of noise. Trials with both fully suppressed static tissue, and with high background intensity (10x the vessel signal, typical for VE-ASL angiography).
The joint-reconstruction approach was further examined by studying the effect of permuting the spokes acquired for each encoding on image quality and the m-PSF. Image quality was assessed using the coefficient of determination, R2, between the ground truth and the reconstruction.

Results

When acquiring the same spokes per encoding, slightly better image quality is achieved for the joint-reconstruction than decode+reconstruct (p << 0.001) (Figure 2a). Reconstruct+decode performed worse than the other methods.
Acquiring different spokes per encoding resulted in clear improvements compared to same spokes (Figure 2b). With the paired 8x4 encoding, the joint-reconstruction method improved compared with the same spokes method (p << 0.001) even in the presence of static tissue signal (Figure 2c). Figure 3 shows examples of these reconstructions.
Permuting the spokes acquired across the paired encodings had small but significant effects on image quality (both worse (Figure 4a) and better (Figure 4c), p << 0.01). The off-diagonal m-PSF entries show small, but discernible differences, whereas the diagonal elements are identical.
The Wiener entropy (spectral flatness) of the non-zero off-diagonals of the m-PSFs was found to correlate with image quality, with high flatness predicting higher R2. The worst reconstruction had flatness 0.409, the medium reconstruction 0.413, and the best 0.414.

Discussion

This examination of sampling-encoding interactions has shown that spreading sampling incoherence across the encoding dimension is beneficial in sparse multi-dimensional reconstructions. While optimal sampling distributions are difficult to predict, m-PSFs provide some information about the sampling/encoding incoherence, and metrics such as Wiener entropy can predict reconstruction fidelity.
We show that in VE-ASL joint reconstruction performs better than decode+reconstruct, or reconstruct+decode. We demonstrate this in a proof-of-principle application, but these ideas could also be applied to other multi-dimensional MR encoding techniques, such as 4D flow imaging⁴.

Acknowledgements

The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). MC (RF201617\16\23) and TO (RF/132) are supported by the Royal Academy of Engineering. SS was supported by funding from the Engineering and Physical Sciences Research Council (EPSRC) and Medical Research Council (MRC) (EP/L016052/1)

References

1. Lustig, Michael, David Donoho, and John M Pauly. “Sparse MRI: The Application of Compressed Sensing for Rapid MR Imaging.” Magnetic Resonance in Medicine58, no. 6, 2007: 1182–95

2. Schauman, S. Sophie, Mark Chiew, and Thomas W. Okell. “Highly Accelerated Vessel-Selective Arterial Spin Labeling Angiography Using Sparsity and Smoothness Constraints.” Magnetic Resonance in Medicine2019 (Online Early View)

3. Candes, Emmanuel, and Justin Romberg. “Sparsity and Incoherence in Compressive Sampling.” Inverse Problems23, no. 3, 2007: 969–85

4. Markl, Michael, Frandics P. Chan, Marcus T. Alley, Kris L. Wedding, Mary T. Draney, Chris J. Elkins, David W. Parker, et al. “Time-Resolved Three-Dimensional Phase-Contrast MRI.” Journal of Magnetic Resonance Imaging17, no. 4, 2003: 499–506

Figures

Figure 1– (A) (B) and (C) show the proposed encoding and sampling methods. The four base components are added/subtracted and radially sampled. (D) (E) and (F) show the corresponding m-PSFs. In method 1 (A,D) the same spokes are acquired 4 times and the m-PSF shows aliasing across components. In method 2 (B, E) 4 sets of different spokes are acquired, and each component affects all other comonents. In method 3 (C,F) each matched sampling pair have the opposite tag-control condition so decoding removes all static tissue contribution. Component 4 does therefore not interact with the others.

Figure 2– Joint-reconstruction (blue) outperforms the separated reconstruction and decoding methods. With fully suppressed background the improvement gained by doing joint-reconstruction is very large, but even with background moderate and statitically significant improvements were measured.

Figure 3– The three decoding and reconstruction approaches produced visibly varying image quality that follows the results presented in Figure 2.

Figure 4– The same spokes sampled across different encodings produced different results. The worst results were acquired by sampling (A) with very colinear spokes for each encoding, and the best by (C) that contained a mixture of close-to-uniform and colinear samplings. (B) is the traditional golden angle sampling for each encoding. The difference in reconstruction quality can potentially be explained by examination of the m-PSFs that are very similar, but have subtle differences.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3683