3675
Experimental demonstration of 3D Cartesian-FRONSAC with new reconstruction approach1Radiology and Biomedical Imaging, Yale University, New Haven, CT, United States
Synopsis
In this work we show the first experimental images, in both phantoms and humans, from 3D Cartesian Fast Rotary Nonlinear Spatial Acquisition (FRONSAC) imaging. FRONSAC adds oscillating nonlinear gradients to a standard Cartesian sequence, such as 3D GRE or MP-RAGE, both of which were acquired for this work. The additional modulation reduces undersampling artifacts and improves response to advanced reconstruction techniques, while maintaining other desirable image characteristics. In addition, we show that a PSF-based reconstruction, a generalization of the approach used in wave imaging, can be applied to FRONSAC data, yielding faster reconstructions that can be highly parallelized.
Introduction
FRONSAC has been recently introduced as a new approach that applies oscillating nonlinear gradients to improve image quality in undersampled MRI. FRONSAC minimally changes the real encoding at each voxel and instead broadens the sampling of k-space along the trajectory. Thus by enhancing a Cartesian sequence with FRONSAC encoding, images retain many Cartesian features while improving undersampled image quality. Previous work has shown significant gains in a wide variety of 2D sequences, both in simulations and experiments. Since the oscillating nonlinear gradients used in FRONSAC vary spatially in 3 dimensions, it is expected that volumetric FRONSAC images will reduce undersampling artifacts in 2 dimensions. Simulations have previously shown that FRONSAC does improve undersampled image quality in various 3D trajectories (1). In this work, we show the first experimentally acquired images which add FRONSAC encoding to standard 3D Cartesian GRE and MP-RAGE sequences. Data was acquired on both phantoms and healthy subjects (n=8), using either 8 channel or 32 channel coil arrays. 3D Cartesian-FRONSAC also presents additional challenges in reconstruction, since the conjugate gradient approaches used in 2D experiments become unwieldy at very large matrix and data sizes. To address this, we developed a PSF-based reconstruction, similar to that used in wave imaging (2), which essentially makes the encoding matrix block diagonal. This approach greatly increases both the efficiency and parallelizability of the reconstruction problem.Methods
Mapping data was acquired at half the image resolution using a gradient mapping analog to chemical shift imaging, which has been previously described (3). For human images, mapping was performed over a rectangular matrix and FOV and subsequently trimmed to the appropriate active volume for each subject. All data was acquired with linear gradients corresponding to a 1283 acquisition with bandwidth 130Hz/pix, but with 8-fold oversampling in the read direction. Read direction was chosen to be HF, to allow for 2D undersampling even with an 8 channel coil. Phantom images were acquired with FRONSAC waveform of 64 cycles per readout on gradient channels C3, S3, and Z2, with amplitudes 298 mT/m^3, 312 mT/m^3, and 42.9 mT/m^3, in triangular analogs to sine, cosine, and sine, respectively. Human images were acquired with FRONSAC waveform of 64 cycles per readout on gradient channels C3, S3, and Z2, with amplitudes 447 mT/m^3, 468 mT/m^3, and 64.4 mT/m^3, in triangular analogs to sine, cosine, and sine, respectively. Images were reconstructed in MATLAB (MathWorks Inc, Natick, Massachusetts, USA) over a 250 mm^3 FOV with imaging matrix size 128^3. Current work is further incorporating compressed sensing reconstruction, which has previously been shown to further enhance FRONSAC encoded data (4).Results
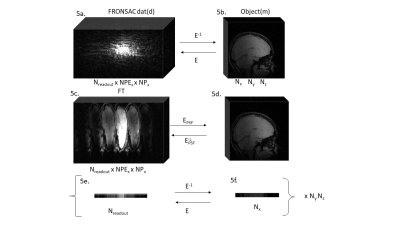
Figure 1 shows the first successful reconstruction of experimental multichannel 3D Cartesian-FRONSAC imaging. The top row shows reference slices from a fully sampled Cartesian sum of squares, and below are the same slices generated from fully sampled Cartesian-FRONSAC data. Figure 2 shows undersampled reconstructions from this data, however, because it was acquired with a lower frequency and amplitude FRONSAC field, image improvements are subtle. Figure 3 shows images of human brain from undersampled (R=2) Cartesian and FRONSAC acquisitions, and Figure 4 shows a similar set of images for an MP-RAGE acquisition. In both these datasets, FRONSAC images show significantly reduced undersampling artifacts. Each of these images were reconstructed with no regularization using the algorithm described below. However, compressed sensing has been previously shown to preferentially improve FRONSAC images, since the undersampling artifacts are made less coherent by the nonlinear encoding, and it is currently being implemented.Figure 5 provides a schematic of the implemented PSF reconstruction approach. In previous work, conjugate gradients are typically applied to solve an encoding problem that regards the entire dataset as encodings of the entire FOV, i.e. data=Em. (Fig 5a-b) However, as noted in previous work (Bilgic, 2015), any encoding that only adds a modulation during the readout while using standard phase encoding between readouts will yield a Fourier transformed image that only modulates the PSF in the read direction. This is observed in Fourier transforms of FRONSAC data, which shows ghosting in the read direction only. (Fig 5c) Thus the Fourier transformed data for each line can be written as a sum of PSFs weighted by the true image density for that line. For parallel imaging, there are Ncoil lines of data related to Ry*Rz spatial rows in the volume. This series of much smaller matrices both reduces the total number of nonzero elements in the reconstruction problem and is also amenable to high parallelization. (5e-f)Conclusion
This work experimentally verifies previously reported simulations which applied FRONSAC encoding to 3D sequences. Preliminary results suggest that the addition of FRONSAC encoding improves undersampling behavior while retaining other features of an imaging sequence. Furthermore, the development of a PSF-based reconstruction improves both the efficiency and parallelizability of the reconstruction problem.Acknowledgements
Special thanks to Terence Nixon from Yale University and Andrew Dewdney from Siemens for their help, and RO1 EB022030 for funding.References
1. Dispenza, N.L., Littin, S., Zaitsev, M. et al. Clinical Potential of a New Approach to MRI Acceleration. Sci Rep 9, 1912; 2019.
2. Bilgic, B. et al. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 2015; 73, 2152–2162.
3. Stockmann J, Ciris P, Galiana G, Tam L, Constable RT. O-Space Imaging: Highly Efficient Parallel Imaging Using Second-Order Nonlinear Fields as Encoding Gradients with No Phase Encoding. Magn Reson Med 2010; 64(2): 447-456.
4. H. Wang, R. T. Constable and G. Galiana, "Accelerate single-shot data acquisitions using compressed sensing and FRONSAC imaging," 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), New York, NY, 2015, pp. 1252-1255.
Figures

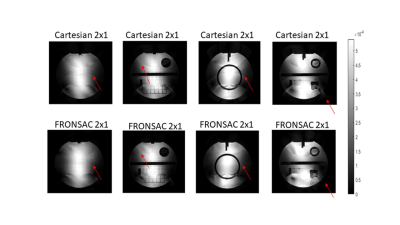
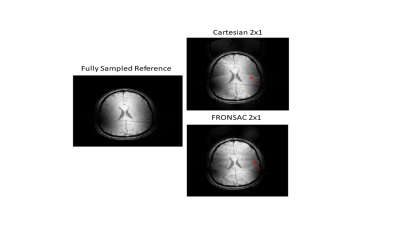
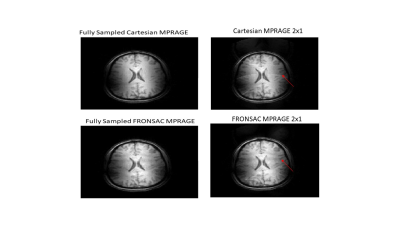
Figure 4. Slices from undersampled 3D Cartesian and Cartesian-FRONSAC MPRAGE scans.