Introduction

Measured MRI phase $$$\theta$$$ is the remainder after modulo division by 2$$$\pi$$$ of the originating phase $$$\phi$$$. As such, images of slowly varying underlying phase often contain abrupt changes (“wraps”), which need to be removed to reveal physical information contained in $$$\phi$$$, such as the local $$$B_0$$$ field. Spatial unwrapping assumes that phase changes in the image which exceed $$$\pi$$$ are indicative of wraps. Region-growing spatial approaches such as PRELUDE [1] divide the volume into regions containing smaller ranges of values and assess phase changes at the borders between them, whereas path-based approaches such as Best Path [2] compare the phase in adjacent voxels, beginning at one location and proceeding to neighboring voxels in an order dictated by one or more weights, such as the spatial phase coherence between voxels. Best Path is faster than PRELUDE but more prone to errors. We propose a new phase unwrapping algorithm, ROMEO, which refines the path-based approach by i) using a number of weights which utilize magnitude as well as phase features to provide improved paths through the object ii) computationally efficient bookkeeping of identified wraps and iii) single-step whole-volume unwrapping of any fourth dimension (echo or time). These features make ROMEO faster and more reliable than PRELUDE and Best Path.

Methods

ROMEO uses up to 3 weights which are multiplied to yield a map of the “quality” of connection between voxels. Unwrapping begins at a seed voxel – that with the highest quality - and unwraps neighbouring voxels with respect to the seed voxel in decreasing order of the quality. The weights are: 1. Spatial phase coherence: $$$ W_{i}^{\theta,Spat}=1-\left|\Omega\left(\theta_i-\theta_j\right)/\pi\right|$$$, where $$$\Omega$$$ is a wrapping operator and i and j are two adjacent spatial locations. 2. Temporal phase coherence: $$$ W_{i}^{\theta,Temp}=\text{max}\left(0,1-\left|\Omega\left(\theta_{i,1}-\theta_{j,1}\right)-\Omega\left(\theta_{i,2}-\theta_{j,2}\right)\cdot TE_1/TE_2\right|\right)$$$. 3. Magnitude coherence: $$$ W_{i}^{M1}=\left(\text{min}\left(M_i,M_j\right)/\text{max}\left(M_i,M_j\right)\right)^2$$$, where $$$M$$$ is the magnitude. Weight 2 is only used for multi-echo or multi-timepoint data and weight 3 is used if magnitude data are available. Best Path deploys the Kruskal algorithm to calculate the Minimum Spanning Tree (MST) [3], using a heap as the priority queue (the order in which voxels are unwrapped), which has a runtime that depends on the number of insertions into the queue (the number of in-mask voxels), n, according to O(n log(n)). ROMEO, which was implemented in Julia [4], used the Prim-Jarník Algorithm [5] with integer representation in a bucket priority queue, the runtime of which scales with O(n). ROMEO was compared to PRELUDE and Best Path using simulated magnitude and phase data of a complex topography [6,7] (matrix size 256x256x256, TE=[4,8,10] ms) as well as in-vivo 7T 3D multi-echo GRE data (matrix size 448x448x112, resolution 0.47x0.47x1.00 mm3, TE=[4,8,12] ms) and time-series EPI of a patient with a brain tumor acquired in a prior study [8] (matrix size 128x128x40, resolution 1.6x1.6x2.3 mm3, TE=22 ms, 57 volumes).

Results

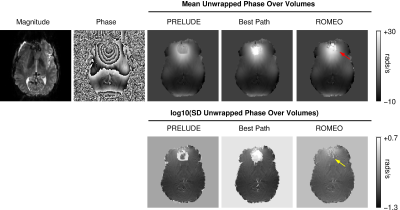
Simulated Data (Fig.1): PRELUDE failed to complete after 13 days. Best Path took 38 s to unwrap the data but made errors. ROMEO was almost twice as fast as Best Path and unwrapped the shape with no errors.
High resolution 7T GRE data (Fig.2): All methods removed phase wraps throughout the brain except in a few voxels in veins. PRELUDE took almost 30 hours to unwrap all 3 echoes, whereas Best Path and ROMEO completed in approximately 30 s. The residual phase wraps inside the veins (see arrows in Fig.2), were largest with Best Path.
57 volumes of 7T fMRI data (Fig.3): PRELUDE took 63 minutes, showed errors in frontal areas which varied widely between volumes, and introduced an average of 0.63 n2$$$\pi$$$ global phase jumps between volumes. Errors were more widespread and more variable between volumes with Best Path, which took 11 seconds, and had an average of 0.14 n2$$$\pi$$$ global phase jumps between volumes. In ROMEO, which was twice as fast as Best Path and introduced no phase jumps between volumes, only a small number of voxels were subject to error, and these were highly consistent between volumes (compare the standard deviation (SD) image at the yellow arrow position in Fig.3).

Conclusions

ROMEO is a rapid and robust phase unwrapping technique that is faster and more reliable than PRELUDE and Best Path. The improvement in accuracy over Best Path comes from the use of weights which better guide the unwrapping through reliable voxels, avoiding noise. Where there is a 4$$$^{th}$$$ dimension in the data (e.g. echoes or time points), over which the phase evolution is expected to be approximately linear, ‘template-based’ unwrapping with respect to the first volume avoids the introduction of n2$$$\pi$$$ phase jumps between these echoes or time points. The improved speed of ROMEO with respect to Best Path comes primarily, though, from efficient handling of values in the queue of voxels to be considered. ROMEO is expected to find application in phase imaging and QSM in challenging cases: at high fields or long echo times, especially close to air spaces or implants.

Acknowledgements

This study was funded by the Austrian Science Fund project FWF31452. BD and SR are supported by Marie Skłodowska-Curie Action: (MRI COMIQSUM 798119, MS-fMRI-QSM 794298 respectively) and KS by ERC Consolidator Grant DiSCo MRI SFN 770939.