3657

Development and validation of a novel finite element inversion method and analysis pipeline for anisotropic MR Elastography
Behzad Babaei1, Daniel Fovargue2, David Nordsletten2,3, and Lynne Bilston1,4
1Neuroscience Research Australia, Sydney, Australia, 2King's College London, London, United Kingdom, 3Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States, 4Prince of Wales Clinical School, University of New South Wales, Randwick, Australia

Synopsis

MR elastography is well established for measuring the mechanical properties of soft tissues in a broad range of clinical populations. However, unlike liver tissue, which is generally considered to be isotropic, muscle is significantly anisotropic, with stiffer mechanical behaviour along the muscle fibre directions. Identifying anisotropic properties is challenging due to the need to track fibre directions and additional numerical difficulties in estimating properties. Here, we describe a novel finite element inversion method for estimating anisotropic mechanical properties of ex vivo tissue data, and validate this method using three sets of simulated data.

Introduction

MR elastography (MRE) has gained substantial use clinically, most commonly for noninvasively detecting liver fibrosis. There has been considerable interest in extending its use to neural and musculoskeletal tissues, however these tissues do not obey the fundamental assumption of most elastography inversion methods, namely isotropy (similar mechanical behaviour in all directions). There has been growing interest in anisotropic MRE methods, but since the governing equations for wave propagation in anisotropic materials include higher-order derivatives, this poses additional numerical challenges for inversion algorithms. In addition, there is a need to identify the local fiber directions (e.g. for muscles or white matter) using DTI or other approaches, and integrate these into the MRE inversion methods. This study describes and validates a novel finite element inversion method and analysis pipeline for anisotropic MRE.

Methods

A novel anisotropic finite element (FE) inversion method was developed by extending an existing divergence free isotropic FE method 1 to solve the transversely anisotropic wave equation. This method enables the combination of multiple input datasets to ensure that adequate wave coverage from different sources fully characterises wave propagation2. The method was validated using simulated data, and then trialled on data from the ex vivo muscle tissue data. Simulated anisotropic elastography data sets were generated using custom finite element software, with a region that has anisotropic viscoelastic properties defined (Gparallel=4kPa, Gperpendicular=2kPa, G"=0.5kPa) embedded within an isotropic region (G’=3kPa, G"=0.5kPa). Displacement data from these simulations was exported and fed into the new inversion software, along with the known anisotropy symmetry axes. Shear moduli parallel and perpendicular to the anisotropic symmetry axes were calculated and compared to the simulation inputs. Next, experimental MRE and DTI data was collected from samples of bovine muscle tissue, using the eXpresso technique (Bovine:F=50Hz, TR/TE=130/9.21ms, 9 slices, voxel size=2mm isotropic3. DTI data was collected with matching geometry (32 directions, b factor=500, TR/TE=3600/60ms). An analysis pipeline was developed to denoise the DTI data using an LPCA method, register the DTI data to anatomical images and magnitude images from the MRE acquisitions using Elastix, and then perform the anisotropic MRE inversion.

Results

Simulation results (Figure 1) show that the new anisotropic inversion method accurately reproduces the input shear moduli, both in the anisotropic region (with constant vertical fibre direction) and the isotropic surrounding region. The simulation of Figure 1 was repeated with varying fibre directions along all 3 dimensions for the anisotropic region (Figure 2). 10% noise was added to the ideal simulation of Figure 2, and the simulation was reconstructed, as shown in Figure 3. Experimental data from the bovine muscle tissue was successfully analysed (Figure 4), and provided anisotropic material properties similar to previous studies on similar samples 4.

Discussion

This new finite element inversion method provides quantitatively correct anisotropic shear moduli for both isotropic and anisotropic regions within a simulated domain, a major step forward in anisotropic MRE. The capacity to input more than one dataset with differing wave propagation directions, such as from multiple wave sources enables more robust parameter estimation, although this is not essential for accurate estimation of properties in skeletal muscles if the vibration sources used sufficiently probe all tissue directions.

Conclusion

Our new anisotropic finite element inversion method is able to robustly extract validated anisotropic viscoelastic mechanical properties from experimental MRE and matched DTI datasets. It is suitable for use in human studies of muscles, and may also have application for other anisotropic soft tissues, such as white matter in the brain.

Acknowledgements

B. Babaei and D. Fovargue contributed equally to this work. This work was supported by a Discovery grant from the Australian Research Council. LEB is supported by an NHMRC senior research fellowship.

References

  1. Fovargue D, Kozerke S, Sinkus R, Nordsletten D. Robust MR elastography stiffness quantification using a localized divergence free finite element reconstruction. Med Image Anal. 2018;44:126-142.
  2. Tweten DJ, Okamoto RJ, Bayly PV. Requirements for accurate estimation of anisotropic material parameters by magnetic resonance elastography: A computational study. Magn Reson Med. 2017;78(6):2360-2372.
  3. Garteiser P, Sahebjavaher RS, Ter Beek LC, et al. Rapid acquisition of multifrequency, multislice and multidirectional MR elastography data with a fractionally encoded gradient echo sequence. NMR Biomed. 2013;26(10):1326-1335.
  4. Qin EC, Sinkus R, Geng G, et al. Combining MR elastography and diffusion tensor imaging for the assessment of anisotropic mechanical properties: a phantom study. J Magn Res Imaging. 2013;37(1):217-226.

Figures

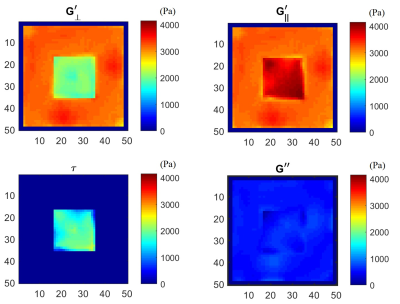
Figure 1: Reconstructed shear moduli for simulation data, using three input datasets with wave propagation in the x,y,z directions. The central square region is anisotropic (wit fibre in x directions), while the surrounding region is isotropic. The panels show the shear modulus perpendicular to the axis of symmetry (G’ꓕ) and parallel to that direction (G’//). τ is the difference between these, and G” is the loss modulus. Good agreement is obtained with the input values of G’ꓕ=2kPa, G’//=4kPa, G"=0.5kPa for the inclusion) and with the surrounding isotropic region (G’=3kPa, G"=0.5kPa)

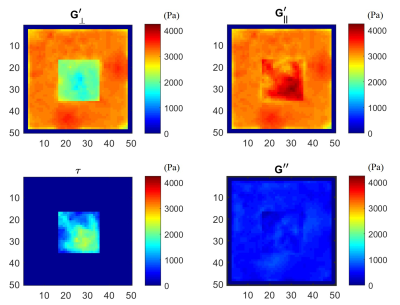
Figure 2: Reconstructed shear moduli for previous simulation data (Figure 1), but with varying fibre directions along all 3 dimensions. Again, good agreement is obtained with the input values of G’ꓕ=2kPa, G’//=4kPa, G"=0.5kPa for the inclusion) and with the surrounding isotropic region (G’=3kPa, G"=0.5kPa)

Figure 3: Reconstructed shear moduli for initial simulation data (Figure 1), with varying fibre directions along all 3 dimensions plus 10% noise. The noise introduced roughly ±1000 Pa artefacts into the reconstruction

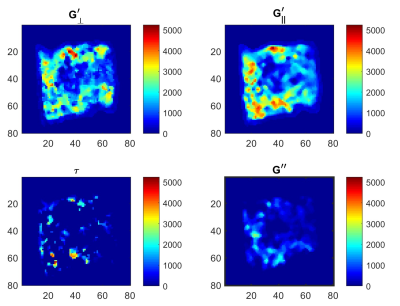
Figure 4: Reconstructed shear moduli for experimental data from bovine muscle. The panels show the shear modulus perpendicular to the muscle fibre direction as identified from DTI (G’ꓕ) and parallel to that direction (G’//). τ is the difference between these, and G” is the loss modulus

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3657