Introduction

The brain MRI is one of the most important methods to diagnose brain diseases. High resolution brain MR images have found significant applications since they can provide detailed structural and anatomical information of the brain tissue. However, it is challenging to obtain high-resolution brain MR images due to limitations such as long acquisition time, small spatial coverage, and low signal to noise ratio. Super-resolution (SR) has been widely applied in recent years. Since SR image reconstruction is an ill-posed problem, many regularization methods have been introduced by formulating the recovery problem as an optimization problem, where different regularizations are used¹. Recently, with the advent of deep learning methods, many SR algorithms based on CNNs have been successfully developed^2,3. However, the limitation of these algorithms is that a large amount of training datasets are required, which are not always available in practice. Deep image prior (DIP) scheme is recently introduced⁴, which shows that the CNN network itself can be considered as a prior on images. However, due to the lack of data-driven prior information, the performance of the DIP method is compromised when the image is severely degraded. Thus, novel deep learning method is urgently needed to overcome these challenges. We propose a new deep learning based super-resolution network, which includes TV as the sparsity prior and the Laplacian⁵ as the sharpness prior, to improve the performance of the original DIP algorithm. We demonstrate that the proposed method is able to recover the high-resolution brain MR images with higher image quality.

Methods

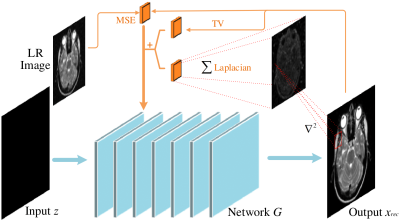
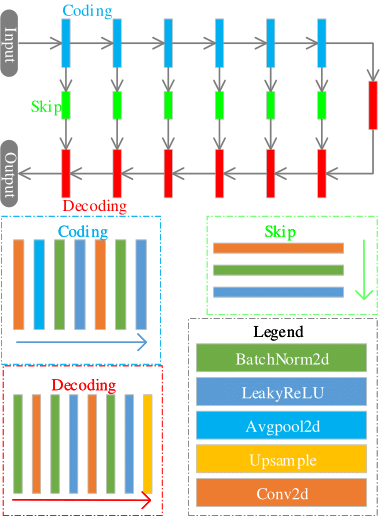
We introduce a novel regularized DIP algorithm to considerably improve the spatial resolution of the brain MR image. The recovery of a high-resolution brain MR image $$$\mathbf X \in \mathbb C^N$$$ from its low-resolution measures $$$\mathbf Y$$$ can be modeled as follows: $$\mathbf Y=f(\mathbf X)+\mathbf n$$
where $$$f$$$ is an arbitrary continuous transformation function that maps the image $$$\mathbf X$$$ to a low-resolution image, and $$$\mathbf n$$$ is the additive noise. The image super-resolution problem can thus be formulated as: $$ \mathbf X^*=\min_{\mathbf X}\|\mathbf Y-f(\mathbf X) \|_2^2 +\lambda {\cal R}(\mathbf X) $$ Where $$${\cal R} (\mathbf X)$$$ is the regularization term, and $$$\lambda$$$ is the balancing parameter. In the DIP scheme, the CNN itself is used as the regularization, which makes the optimization problem for DIP as follows: $${\theta}^*=\min_{\theta} \|\mathbf y-f(N_{\theta}(\mathbf Z))\|^2_2;\;\rm{s.t.}\mathbf X=N_{{\theta}^*}(\mathbf Z)$$ Here, $$$N_{\theta}$$$ is the deep neural network parameterized by $$$\theta$$$. The input of the network is a noise vector $$$\mathbf Z$$$. Due to the lack of training data, the DIP scheme has sub-optimal performance when the downsampling factor is large. We propose to include total variation (TV) and the Laplacian in the DIP framework to promote the piecewise-smoothness and the sharp features of the image. We formulate the proposed method as follows: $${\theta}^*=\min_{\theta}\|\mathbf Y-f(\mathbf X)\|^2_2 +\lambda_1 {\cal R}_{\rm{TV}}(\mathbf X) +\lambda_2 {\cal R}_{\rm{Laplacian}}(\mathbf X)$$ Here $$$\mathbf X=N_{{\theta}^*}(\mathbf Z)$$$, $$${\cal R}_{\rm{TV}}(\mathbf X)=\sum\limits_{i=1}^N\sqrt{|D_x|^2+|D_y|^2}$$$ is the TV regularization, where $$$D_x$$$ and $$$D_y$$$ are the finite difference operators along $$$x$$$ and $$$y$$$ dimensions. $$${\cal R}_{\rm{Laplacian}}(\mathbf X)=\sum\limits_{i=1}^N|\nabla^2\mathbf X| $$$ is the Laplacian regularization. $$$\lambda_1$$$ and $$$\lambda_2$$$ are balancing parameters. Fig.1 shows the implementation block diagram of the proposed algorithm. Here, we use a UNet-based network architecture, illustrated in Fig.2. Note that the TV and Laplacian priors, along with the difference between the low-resolution image and the output image, are incorporated in the network. The detailed illustration of the network is shown in the caption of Fig.2. We use zero-filled images as the input of the network. Note that the proposed network itself is used as a prior. By including the TV and Laplacian penalties, the method is able to promote the sparsity and the sharpness of the recovered image.

Results and discussion

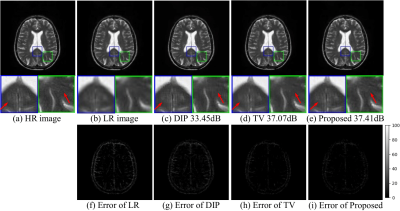
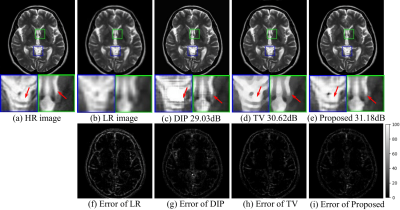
In order to evaluate the performance of the proposed method, we generate low-resolution images from the high-resolution brain MR images. The SR results are compared with the high-resolution ground truth. The comparison methods are standard TV, original DIP scheme, and the proposed method. The results from different methods with downsampling factor of 2 and 4 are shown in Fig3 and Fig4, respectively. The results show that the proposed method outperforms the other methods by preserving more detailed features and having lower errors.

Conclusion

We proposed a novel brain MR image super-resolution deep-learning-based framework. The proposed method exploits the fitting ability of the network itself, which requires no pre-training image pairs. By including the TV and the Laplacian as the image feature priors, we are able to obtain improved results. Super-resolution of the brain MR images with downsampling factors 2 and 4 demonstrate the benefits of the proposed method.

Acknowledgements

No acknowledgement found.