3635

Learning-based Optimization of the Under-sampling PattErn with Straight-Through Estimator (LOUPE-ST) for Fast MRI

Jinwei Zhang^1,2, Hang Zhang^2,3, Cagla Deniz Bahadir⁴, Alan Wang³, Mert Rory Sabuncu^1,2,3, Pascal Spincemaille², Thanh D. Nguyen², and Yi Wang^1,2
¹Biomedical Engineering, Cornell University, Ithaca, NY, United States, ²Weill Cornell Medicine, New York, NY, United States, ³Electrical and Computer Engineering, Cornell University, Ithaca, NY, United States, ⁴Siemens Healthineers, Princeton, NJ, United States

Synopsis

In this work, we propose LOUPE-ST, which extends the previously introduced optimal k-space sampling pattern learning framework called LOUPE by employing a straight-through estimator to better handle the gradient back-propagation in the binary sampling layer and incorporating an unrolled optimization network (MoDL) to reconstruct T2w images from under-sampled k-space data with high fidelity. Our results indicate that, compared with the variable density under-sampling pattern at the same under-sampling ratio (10%), superior reconstruction performance can be achieved with LOUPE-ST optimized under-sampling pattern. This was observed for all reconstruction methods that we experimented with.

Introduction

One major task in compressed sensing MRI is designing a random under-sampling pattern, which can be controlled by a variable-density probabilistic density function. However, designing ‘optimal’ random sampling pattern is still an open problem. In this work, we extended the previously introduced LOUPE (1) framework by modifying both the reconstruction network to an unrolled quasi-Newton network (3) in order to reconstruct multi-coil data properly and inserting a Straight-Through (ST) estimator (2) into the binary sampling layer to avoid zero gradients when back-propagating to this layer.

Data acquisition and processing

Fully sampled k-space data were acquired in 4 subjects (3 training and 1 test) using a sagittal T2 weighted variable flip angle 3D fast spin echo sequence on a 3T GE scanner with a $$$32$$$-channel head coil. Imaging parameters were: $$$ 256 \times 256 \times 192$$$ imaging matrix size, $$$ 1 mm^3 $$$ isotropic resolution. Coil sensitivity maps of each axial slice were calculated with ESPIRiT (4) using a centric $$$ 25 \times 25 \times 32$$$ k-space region. From the fully sampled data, a coil combined image using the same coil sensitivity maps was obtained to provide the ground truth label for both network training and reconstruction performance comparison. The central 100 slices of each subject were extracted for the training (300 slices) and test (100 slices) datasets. In addition, k-space under-sampling was deployed in the ky-kz plane retrospectively in all the following experiments.

Network architecture

Figure 1 shows the proposed network architecture consisting of two sub-networks: one sampling pattern learning network and one reconstruction network. In the sampling pattern learning network, weights $$$w$$$ are trainable parameters to generate a renormalized probabilistic mask $$$P = \text{Renormalize}(\frac{1}{1+\text{exp}(-a \cdot w)})$$$, where $$$a$$$ is the slope factor and $$$\text{Renormalize}(\cdot)$$$ is a linear scaling operation to enforce $$$\bar{P} = \gamma$$$ (the preset under-sampling ratio). After obtaining $$$P$$$, a binary mask $$$U$$$ is sampled as $$$1_{z < P}$$$, where $$$z$$$ is an independent random sample from $$$[0, 1]$$$ uniformly distributed random vector with the same dimension as $$$P$$$. This binary mask $$$U$$$ is sampled at every forward pass in the network and once generated, it is used to under-sample the fully sampled multi-coil k-space data as shown in Figure 1. For the reconstruction network, the unrolled quasi-Newton network of MoDL (3) is used. In MoDL, Denoiser + Data consistency blocks are replicated $$$K$$$ times to mimic the optimization procedure and the network’s weights are shared among blocks. Zero-filling reconstruction $$$x^{(0)}$$$ is connected to all the data consistency sub-blocks to deploy $$$L_2-$$$regularized optimization, which also works as the skip connection to benefit the training of $$$w$$$.

Straight-Through (ST) for binary mask

One major issue in training the proposed network is that the random sampling with step function used to generate the binary under-sampling mask introduces zero gradients almost everywhere during back-propagation, rendering updates to the probabilistic mask weights $$$w$$$ useless. To overcome this issue, a Straight-Through (ST) estimator (2) was used to back-propagate through such stochastic neurons of the binary mask layer. The ST estimator replaces the derivative factor used during backpropagation, $$$\frac{d 1_{z < P}}{dw} = 0$$$, with the following one: $$\frac{d 1_{z < P}}{dw} = \frac{dP}{dw}$$ which has better gradient characteristics for parameters learning. This biased estimator was proposed in (2) by adapting from Hinton’s lecture 15b (5), where $$$\frac{d 1_{z < P}}{dw} = 1$$$ was firstly proposed to deal with stochastic neurons. In this work, we used the above equation as the gradient estimator for binary mask neurons.

Experimental details

We chose $$$a = 0.25, \ \gamma = 10\% \ \text{and} \ K = 2$$$. Two sub-networks were trained simultaneously from scratch by minimizing $$$L_1$$$ loss: $$$ \Sigma_{k=1}^{K} \|x_j^{(k)} - t_j\|_1$$$, where $$$x_j^{(k)}$$$ denotes $$$k\text{th}$$$ intermediate reconstruction of $$$j\text{th}$$$ training data, with $$$t_j$$$ the fully sampled label/target. After convergence, a specific binary mask was generated from well-trained $$$P$$$ and fixed to further train the reconstruction network alone. We implemented in PyTorch with Python version 3.7.3, using the Adam optimizer (7), together with batch size $$$4$$$, number of epochs $$$100$$$ and initial learning rate $$$1\times10^{-3}$$$. CG-ESPIRiT (4) and TVG (6) reconstructions were also performed and compared.

Results

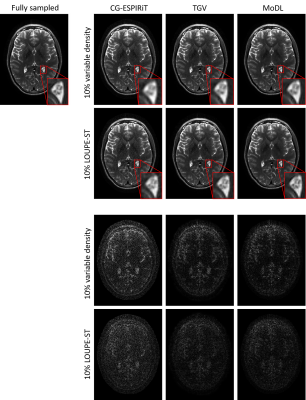
Figure 2 shows variable density sampling pattern and LOUPE-ST optimized sampling pattern. The latter appears more uniform and samples more peripheral k-space locations.

Figure 3 shows reconstruction results using two sampling patterns in Figure 2. For each reconstruction method, LOUPE-ST optimized sampling pattern captures better image depictions with sharper tissue boundaries and less global errors than variable density sampling pattern.

Table 1 shows average PSNR (dB) and the corresponding standard deviations of all 100 test slices with respect to the fully sampled labels. The PSNR of LOUPE-ST optimized sampling pattern was higher than that of the variable density one ($$$p < 0.05$$$, t-test) for each reconstruction method.

Discussion and conclusion

Building on the recently proposed LOUPE framework (1), a new optimal under-sampling pattern learning method, LOUPE-ST, was presented. LOUPE-ST uses a straight-through estimator for updating the sampling pattern of compressed sensing parallel imaging in MRI and an unrolled reconstruction network. Experimental results show LOUPE-ST provides better sampling pattern compared to manually tuned variable density pattern in $$$10\%$$$ sampling ratio. Future work includes implementing LOUPE-ST optimized sampling pattern into a T2w sequence and accelerating MR scans prospectively.

Acknowledgements

We thank Dr. Adrian Dalca from A.A. Martinos Center for Biomedical Imaging regarding his idea of renormalizing the probabilistic mask before binary sampling.

References

1. Bahadir CD, Dalca AV, Sabuncu MR. Learning-based Optimization of the Under-sampling Pattern in MRI. 2019. Springer. p 780-792.

2. Bengio Y, Léonard N, Courville A. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv preprint arXiv:13083432 2013.

3. Aggarwal HK, Mani MP, Jacob M. Modl: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging 2018;38(2):394-405.

4. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic resonance in medicine 2014;71(3):990-1001.

5. Hinton G, Srivastava N, Swersky K. Neural networks for machine learning. Coursera, video lectures 2012;264.

6. Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magnetic resonance in medicine 2011;65(2):480-491.

7. Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:14126980 2014.

Figures

Figure 1. Proposed network architecture consisting of an under-sampling network and a K-unrolled reconstruction network. In the under-sampling network, a binary mask $$$U$$$ is sampled from renormalized probabilistic mask $$$P$$$ with trainable parameters $$$w$$$. In the reconstruction network, denoiser + data consistency blocks are repeated K times, and coil sensitivity maps and zero-filling reconstruction are skip-connected into the data consistency layer which also benefits the training of $$$w$$$. The straight-through estimator is used during back-propagation.

Figure 2. LOUPE-ST optimized sampling pattern and the variable density pattern in $$$10\%$$$ under-sampling ratio. Compared to the variable density sampling pattern, LOUPE-ST optimized pattern appears more uniform and picks more peripheral k-space locations. Fully sampled centric k-space regions are used to calculate coil sensitivity maps.

Figure 3. Reconstruction results (first two rows, window [0, 0.5]) of three methods using variable density sampling pattern and LOUPE-ST optimized sampling pattern from Figure 2. Using the variable density pattern, tissue boundaries were blurry (zoomed-in insets) with considerable global errors (last two rows, window [0, 0.1]). TGV and MoDL showed comparable and better reconstruction quality compared to CG-ESPIRiT.

Table 1. Average PSNRs (dB) ± standard deviations of 100 test slices reconstructed by each method in both under-sampling patterns. Statistical t-test was deployed between variable density and LOUPE-ST optimized sampling pair for each method ($$$*$$$ means significantly different with $$$p < 0.05$$$). LOUPE-ST optimized sampling pattern improved the reconstruction results considerably compared to the variable density pattern.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3635