3628
Derivation of quantitative T1 map from a single MR image using a self-attention deep neural network1Radiation Oncology, Stanford University, Stanford, CA, United States, 2Radiology, University of California San Diego, La Jolla, CA, United States
Synopsis
The application of quantitative MRI is limited by additional data acquisition for variable contrast images. Leveraging from the unique ability of deep learning, we propose a data-driven strategy to derive quantitative T1 map and proton density map from a single qualitative MR image without specific requirements on the weighting of the input image. The quantitative parametric mapping tasks are accomplished using self-attention deep convolutional neural networks, which make efficient use of local and non-local information. In this way, qualitative and quantitative MRI can be attained simultaneously without changing the existing imaging protocol.
INTRODUCTION
Quantification of tissue properties is imperative for tissue characterization. However, the adoption of current quantitative MRI approaches is hindered by the involvement of extra data acquisition for variable contrast images. In this study, we propose a deep learning strategy to extract quantitative tissue relaxation parametric maps (of T1 and proton density) from a single qualitative image without special requirement on the weighting of the input image. In this way, qualitative and quantitative MRI are acquired simultaneously without any additional data acquisition. The method is mainly validated in T1 mapping cartilage MRI.METHODS
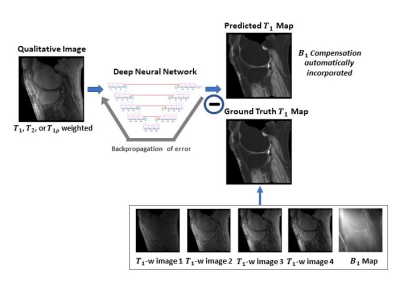
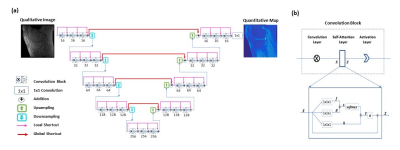
To provide end-to-end mappings from a single qualitative image to the corresponding T1 map and proton density map, convolutional neural networks are employed. In the training of a deep neural network, input images are T1, T1r, or T2 weighted images acquired using a specific ultra-short TE sequence 1-3; meanwhile, ground truth T1 maps is obtained, each from a series of T1 weighted variable flip angle images and a map. With the difference between the predicted maps and the ground truth backpropagated, network parameters are updated using the Adam algorithm. This iterative procedure continues until convergence is reached, as illustrated in Figure 1. For a test image acquired using the same imaging protocol, T1 map is automatically generated by the established network model. Notice that since B1 compensation is built into the network model, the need for B1 map measurement is mitigated in T1 mapping.Similarly, convolutional neural networks are employed for proton density mapping, where ground truth proton density map is calculated from a single T1 weighted image and the corresponding T1 map. A special convolutional neural network is constructed for the proposed quantitative parametric mapping. The network has a hierarchical architecture, composed of an encoder and a decoder 4. This enables feature extraction at various scales while enlarging the receptive field at the same time. A unique shortcut pattern is designed, where global shortcuts (that connect the encoder path and the decoder path) compensate for details lost in down-sampling, and local shortcuts (that forward the input to a hierarchical level of a single path to all subsequent convolutional blocks) facilitate residual learning. Attention mechanism is incorporated into the network to make efficient use of non-local information 5-7. Briefly, in self-attention, direct interactions are established between all voxels within a given image, and more attention is focused on regions that contain similar spatial information. In every convolutional block, a self-attention layer is integrated, where the self-attention map is derived by attending to all the positions in the feature map obtained in the previous convolutional layer. The value at a position of the attention map is determined by two factors. One is the relevance between the signal at the current position and that at other positions, defined by an embedded Gaussian function. The other is a representation of the feature value at the other position, given by a linear function. Here, weight matrices are identified by the model in training. The proposed network is shown in Figure 2.
Deep neural networks are trained for T1 mapping and proton density mapping, each taking single images with a specific T1, T1r or T2 weighting as input. A total of 1,224 slice images from 51 subjects (including healthy volunteers and patients) are used for model training, and 120 images of 5 additional subjects are employed for model testing.
RESULTS
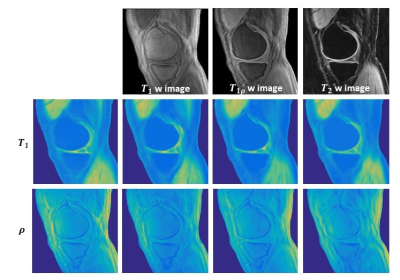
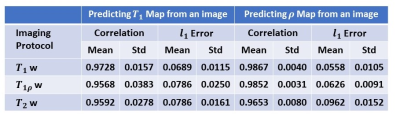
Using established models, quantitative T1 and proton density maps are predicted from each single test image with specific weighting. Figure 3 shows a representative case. The predicted images show high fidelity to the ground truth maps. Specifically, from T2 or T1r weighted images, T1 map is extracted with high sensitivity, although the influence of the T1 component has been intentionally suppressed. The evaluation results using quantitative metrics are shown in Figure 4.DISCUSSION
In the proposed deep learning strategy, quantitative tissue parametric maps are extracted from a single qualitative image with the aid of a priori knowledge casted in a pre-trained deep learning model. Deep neural network has unprecedented ability of learning complex relationships and incorporating existing knowledge into the inference model through feature extraction and representation learning. A significant practical benefit of the proposed method is that no additional scans are required for generating quantitative parametric maps. Because there is no special requirement on the imaging protocol used for input image acquisition, large number of quantitative parametric maps can be derived from single qualitative images obtained in standard clinical practice or biomedical research, facilitating quantitative image analysis and data sharing in various prospective and retrospective studies.CONCLUSION
We present a new data-driven strategy for quantitative tissue parametric mapping. Using properly trained deep learning models, quantitative T1 and proton density maps can be predicted from a single MR image with high accuracy achieved.Acknowledgements
This research is partially supported by NIH/NCI (1R01 CA176553), NIH/NIAMS (1R01 AR068987), NIH/NINDS (1R01 NS092650).References
1. Y. J. Ma, W. Zhao, L. Wan, T. Guo, A. Searleman, H. Jang, et al., "Whole knee joint T1 values measured in vivo at 3T by combined 3D ultrashort echo time cones actual flip angle and variable flip angle methods," Magnetic resonance in medicine, vol. 81, pp. 1634-1644, 2019.
2. Y.J. Ma, M. Carl, A. Searleman, X. Lu, E. Chang, and J. Du, "3D adiabatic prepared ultrashort echo time cones sequence for whole knee imaging," Magnetic Resonance in Medicine, vol. 80, pp. 1429-1439, 2018.
3. Du, J., Diaz E, Carl M, Bae W, Chung CB, Bydder GM, Ultrashort echo time imaging with bicomponent analysis. Magnetic resonance in medicine, 2012. 67(3): p. 645-649.
4. Y. Wu, Y. Ma, D. P. Capaldi, J. Liu, W. Zhao, J. Du, et al., "Incorporating prior knowledge via volumetric deep residual network to optimize the reconstruction of sparsely sampled MRI," Magnetic resonance imaging, 2019.
5. Wu, Y., Y. Ma, J. Liu, W. Zhao, J. Du et al., Self-attention convolutional neural network for improved MR image reconstruction. Information Sciences, 2019. 490: p. 317-328.
6. Vaswani, A., et al. Attention is all you need. in Advances in Neural Information Processing Systems. 2017.
7. Zhang, H., et al., Self-attention generative adversarial networks. arXiv preprint arXiv:1805.08318, 2018.
Figures