Introduction

Despite the excellent spatial resolution and soft tissue contrast, clinical MRI suffers from the intrinsic limitation of generally long scan time. In practice, partial Fourier data acquisition is often performed along phase encoding direction and frequency encoding direction to accelerate scan and shorten echo time, respectively. Subsequently missing k-space data are often estimated using the projection onto convex sets (POCS) method¹, yet its performance is suboptimal in presence of rapid image phase variations especially when partial Fourier fraction is low. Recently, deep learning algorithms including deep convolutional neural networks (CNNs) are entering the field of MRI reconstruction and demonstrate great potential in parallel imaging reconstruction, noise and artifact suppression^2-5. In this study, we aimed to develop a deep learning approach for robust partial Fourier reconstruction. We designed a CNN model and trained it using large human knee datasets. The results demonstrated that our method was robust and outperformed the existing POCS method.

Method

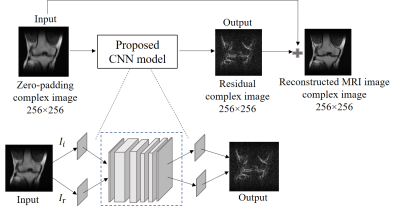
CNN Model
The CNN model is illustrated in Figure 1. It has five convolutional layers and each layer is followed by the batch normalization layer and the activation function – Rectified Linear Unit (ReLU), due to its nonlinear characteristics. The real and imaginary parts of the original images act as two channels of the input for the network. Similarly, the two channels of the output are the real and imaginary parts of the predicted residual. The training and testing processes were implemented using PyTorch 1.0 on a Linux workstation (Intel Xeon(R) E5-1620 v4 CPU, 64GB RAM and two NVIDIA GTX 1080ti GPUs).

Data preparation, CNN training and testing
For model training, validation and testing, we employed the large and original knee datasets from the Center for Advanced Imaging Innovation and Research (CAI2R) at NYU School of Medicine and NYU Langone Health⁶. They were complex single-channel coronal proton density-weighted knee image datasets obtained from 1500 normal subjects on 3T and 1.5T clinical MRI scanners. For each subject dataset, images from 20 consecutive slice locations were extracted. The complex images were then resized to 256×256. The resulting 30,000 images (1500×20) were divided into three groups, i.e., 70% for training, 15% for validation, and 15% for testing, respectively. The performance of our CNN model and existing POCS method were compared for different partial Fourier fractions that varied from 0.65 to 0.51 along the frequency encoding or phase encoding direction. For frequency encoding partial Fourier, we examined the partial Fourier fractions of 0.65, 0.55 and 0.51. For phase encoding partial Fourier, we examined the partial Fourier fractions of 0.6 and 0.55. To further evaluate the robustness of the CNN model trained with the complex human knee proton-density-weighted images as described above, we applied and evaluated its performance in partial Fourier reconstruction of the brain T1-weighted gradient-echo (GE) and T2-weighted fast spin echo (FSE) image datasets acquired on a separate 3T Philips MRI scanner.

Results

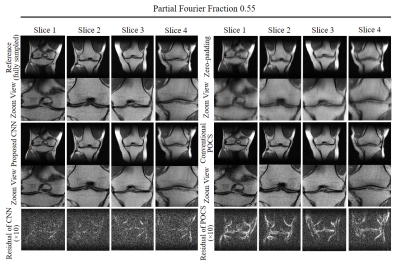
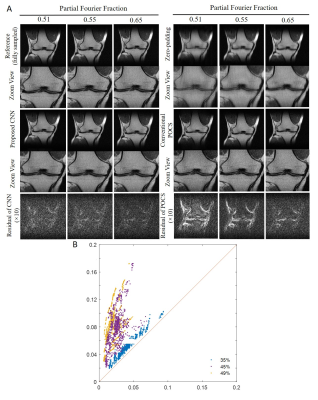
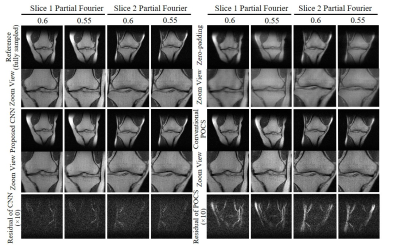
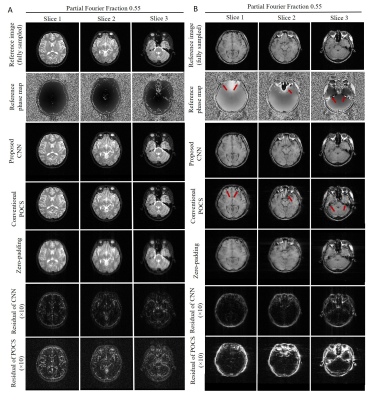
Figure 2 shows the typical reconstruction results by the proposed CNN method and existing POCS methods for partial Fourier faction of 0.55 along the frequency encoding direction (vertical). Figure 3 compares the performance of POCS and CNN methods at partial Fourier fractions of 0.65, 0.55 and 0.51 (nearly half-Fourier) along frequency encoding direction (vertical), together with the residual image root mean square error (RMSE) analysis of POCS and CNN results from all 800 test image datasets. Figure 4 compares the performance of the two methods at partial Fourier fractions of 0.6 and 0.55 along the phase encoding direction (horizontal). These results clearly demonstrated that the proposed CNN method performed better than the POCS method, especially in preserving high frequency image information without amplifying noise. Figure 5 shows the partial Fourier reconstruction of brain images using the knee-image-trained CNN model at partial Fourier fraction of 0.55 along the vertical phase encoding direction (Figure 5A) and along the horizontal frequency encoding direction (Figure 5B), again demonstrating the superior and robust performance of the proposed CNN method over POCS.

Discussion and conclusions

This study demonstrated a new deep learning approach for the partial Fourier MRI reconstruction using convolutional neural networks. The proposed CNN model is based on the complex image residual map prediction from the complex image directly reconstructed by zero-padding the missing k-space data. The experimental results indicated that this CNN approach robustly reconstructed partial Fourier k-space data by recovering high frequency image information/structures without noise amplification even when partial Fourier fraction approached 0.5 (i.e., half-Fourier), significantly outperforming the traditional POCS method. Further, knee-image-trained CNN model were also successfully demonstrated to be applicable to partial Fourier reconstruction of other organ images with different contrasts (i.e., brain T2-weighted FSE images as well as the T1-weighted GE images where rapid local phase variations often occur). Future studies will focus on the optimization and evaluation of various CNN models for reconstruction accuracy and robustness.

Acknowledgements

This study is supported in part by Hong Kong Research Grant Council (C7048-16G and HKU17115116 to E.X.W.), Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) and Guangdong Key Technologies for Alzheimer's Disease Diagnosis and Treatment (2018B030336001) to E.X.W.