3623
k-t CNN for Modeling Spatio-temporal Mappings and an Application to Reconstruction of k-space Data with Stack-of-spirals Trajectory1Advanced Technology Research Department, Research and Development Center, Canon Medical Systems Corporation, Kanagawa, Japan, 2MRI Systems Development Department, MRI Systems Division, Canon Medical Systems Corporation, Kanagawa, Japan
Synopsis
The authors propose a new model using a convolutional neural network (CNN) named k-t CNN for approximating non-linear spatio-temporal mappings used in various applications. Existing studies imply that spatio-temporal mappings are non-linear. Most existing studies developed various methods using linear models for spatio-temporal applications. Meanwhile, the effectiveness of non-linear models was shown for spatial-domain applications.
As an application of k-t CNN, the effectiveness of the proposed method is shown experimentally in the case of reconstruction of stack-of-spirals k-space data.
INTRODUCTION
There exist many studies related to reconstruction of spatio-temporal MR images including acceleration of acquisition of dynamic MR images using highly under-sampled k-space data1-7. These studies assume that MR images can be modeled as sets of spatio-temporal mappings, which include signals in the Fourier-transformed time-domain1,2, total-variation3, wavelet3, partially separable functions4, principle component5,6, and principle component with residual signal7.A set of spatio-temporal mappings can be defined as a mapping from an input k-t image to an output k-t image. A k-t image is a set of time-series images reconstructed from the acquired k-space data. A k-t image can include multiple resolutions in both spatial and temporal directions.
Existing studies imply that spatio-temporal mappings are non-linear. Most existing studies developed various methods using linear models for spatio-temporal applications. Meanwhile, the effectiveness of non-linear models was shown for spatial-domain applications8,9.
The authors propose a new model using a convolutional neural network (CNN)10 named k-t CNN for modeling a spatio-temporal mapping named a k-t mapping. CNNs are known as an effective model to represent non-linear mappings and have been used in various applications. K-t CNN is defined as a mapping from time-series MR images with noises to images without noise. It is an extension of the CNN framework with multiple inputs and one output11,12.
As an application of k-t CNN, the effectiveness of the proposed method is shown experimentally in the case of reconstruction of stack-of-spirals k-space data.
THEORY
The goal of this research is to find a universal model of a k-t mapping $$$y=f(x)$$$ from the input k-t image $$$x$$$ with noise to the output k-t image $$$y$$$ without noise, as shown in Figures 1(a) and 1(b). A model for approximating $$$f(x)$$$ needs to be sufficiently flexible since $$$f(x)$$$’s can be described by various non-linear mappings depending on applications.The authors propose k-t CNN which uses a CNN for approximating $$$f(x)$$$. The function $$$f(x)$$$ is approximated as $$$C(x;p)$$$ where $$$C$$$ is a CNN and $$$p$$$ is a set of trainable parameters as shown in Figure 1(c).
METHODS
To compare k-t CNN with an existing CNN-based method, k-t CNN is evaluated for the reconstruction of dynamic MR images using a stack-of-spirals trajectory. The reconstruction using k-t CNN consists of gridding processes in multiple temporal resolutions and a denoising process which applies k-t CNN to the outputs of gridding, as shown in Figure 2. As a conventional method, a CNN with one-frame input and one-frame output is also evaluated.For sampling simulation, 8 volunteer images (7 training and 1 test) were acquired with T1-weighted, Cartesian trajectory, $$$256 \times 256 \times 32$$$, 24 frames, and additional navigation signals. They were sorted retrospectively using the navigator signals and reconstructed as dynamic ground-truth images. A set of k-space data were generated by applying a non-uniform FFT with stack-of-spirals trajectory to the ground-truth images. The reduction factor is set to 1 until the radius of a spiral reached to 14% of k-max, and set to 6 otherwise. For each spiral, 8192 points are sampled. The CNNs were trained by adaptive moment estimation (Adam) with a mean-squared-error loss function. The number of epochs was 50.
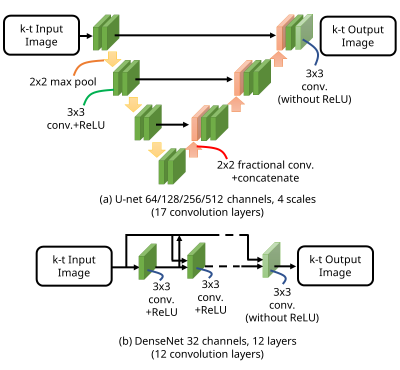
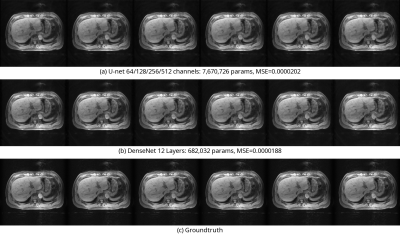
The first experiment compares k-t CNN using U-net13 with 4 spatial scales and DenseNet14 with 12 layers as $$$C(x;p)$$$. The CNNs used in the experiment are shown in Figure 3. The number of parameters are 7,670,726 for U-net and 682,032 for DenseNet. In this experiment, 4 temporal resolutions (1, 2, 4, 6 spirals/frame) were used.
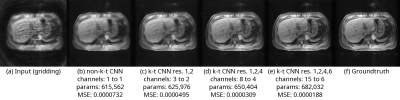
The second experiment compares k-t CNN using 4 combinations of temporal resolutions as inputs. The combinations are 1 spirals/frame (i.e. a conventional method); 1, 2 spirals/frame; 1, 2, 4 spirals/frame; and 1, 2, 4, 6 spirals/frame. In this experiment, DenseNet was used as $$$C(x;p)$$$.
RESULTS
The results of the first experiment are shown in Figure 4. While the number of parameters in DenseNet is significantly lower than that in U-net, the results show that both networks reconstructed images whose MSE and subjective quality were comparable.The results of the second experiment are shown in Figure 5. A conventional CNN did not suppress the artifacts of the reconstructed k-t image. By increasing the number of temporal resolutions, the strength of artifacts became weaker while only a slight number of parameters were added.
DISCUSSION
K-t CNN gives a theoretical interpretation for a generalized model of recent methods11,12. The studies of these methods explained nothing about theoretical aspects of k-t mappings.K-t CNN can be applied not only to delay-aware reconstructions but to other applications. These studies limited the number of CNN outputs to one since their aim was solely for low-delay reconstruction.
K-t CNN can be used in conjunction with other methods. For example, k-t CNN can be used with unrolled iterative reconstruction such as ADMM-Net15. In addition, it is possible to apply k-t CNN to non-reconstruction applications. Applications to other methods or applications remain as future works.
CONCLUSION
The authors propose k-t CNN to approximate non-linear k-t mappings used in various applications. As an application of k-t CNN, the effectiveness of the proposed method is shown experimentally in the case of reconstruction of stack-of-spirals k-space data.Acknowledgements
No acknowledgement found.References
1. Madore B, Glover GH, Pelc NJ. Unaliasing by Fourier-encoding the overlaps using the temporal dimension (UNFOLD), applied to cardiac imaging and fMRI. Magn Reson Med 1999; 42: 813-828.
2. Tsao J, Boesiger P, Pruessmann KP. k-t BLAST and k-t SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn Reson Med 2003; 50: 1031-1042.
3. Lustig M, Santos JM, Donoho DL, Pauly JM. k-t SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity. Proc. ISMRM 2006; 14: 2420.
4. Liang Z. Spatiotemporal imagingwith partially separable functions. Proc. IEEE Intl. Sym. Biomed. Imag. 2007; 988-991.
5. Pedersen H, Kozerke S, Ringgaard S, Nehrke K, Kim WY. k-t PCA: Temporally constrained k-t BLAST reconstruction using principal component analysis. Magn Reson Med 2009; 62: 706-716.
6. Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Transactions on Medical Imaging 2011; 30 (5):1042-1054.
7. Otazo R, Candes E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med 2015; 73: 1125-1136.
8. Chang Y, Liang D, Ying L. Nonlinear GRAPPA: A kernel approach to parallel MRI reconstruction. Magn Reson Med 2012; 68: 730-740.
9. Akcakaya M, Moeller S, Weingartner S, Ugurbil K. Scan-specific robust artificial-neural-networks for k-space Interpolation (RAKI): database-free deep learning reconstruction for fast imaging. Proc. Joint Annual Meeting ISMRM-ESMRMB 2018; 576.
10. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE 1998; 86 (11): 2278-2324.
11. Takeshima H. Integrating spatial and temporal correlations into a deep neural network for low-delay reconstruction of highly undersampled radial dynamic images. Proc. Joint Annual Meeting ISMRM-ESMRMB 2018; 2796.
12. Takeshima H, Kutsuna H. Fast acquisition and low-delay reconstruction of stack-of-stars trajectory using temporal multiresolution images and a convolutional neural network. Proc. ISMRM 2019; 467.
13. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Proc. Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2015; 234-241.
14. Huang G, Liu Z, Maaten L, Weinberger KQ. Densely Connected Convolutional Networks. Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017; 2261-2269.
15. Yang Y, Sun J, Li H, Xu Z. ADMM-Net: A Deep Learning Approach for Compressive Sensing MRI. arXiv preprint 2017; arXiv:1705.06869.Figures