3621
Reconstructing non-Cartesian acquisitions using dAUTOMAP
Maarten L Terpstra1,2, Federico d'Agata1,2,3, Bjorn Stemkens1,2, Jan JW Lagendijk1, Cornelis AT van den Berg1,2, and Rob HN Tijssen1,2
1Department of Radiotherapy, Division of Imaging & Oncology, University Medical Center Utrecht, Utrecht, Netherlands, 2Computational Imaging Group for MR diagnostics & therapy, Center for Image Sciences, University Medical Center Utrecht, Utrecht, Netherlands, 3Department of Neurosciences, University of Turin, Turin, Italy
1Department of Radiotherapy, Division of Imaging & Oncology, University Medical Center Utrecht, Utrecht, Netherlands, 2Computational Imaging Group for MR diagnostics & therapy, Center for Image Sciences, University Medical Center Utrecht, Utrecht, Netherlands, 3Department of Neurosciences, University of Turin, Turin, Italy
Synopsis
Recently, dAUTOMAP has been presented to perform deep learning-based image reconstruction. dAUTOMAP uses gridded k-space points and so far it has only been used to reconstruct Cartesian acquisitions. In this work, we demonstrate that dAUTOMAP can produce high-quality reconstructions on radial and spiral non-Cartesian acquisitions and can resolve artifacts beyond those introduced by the undersampled acquisition.
Introduction
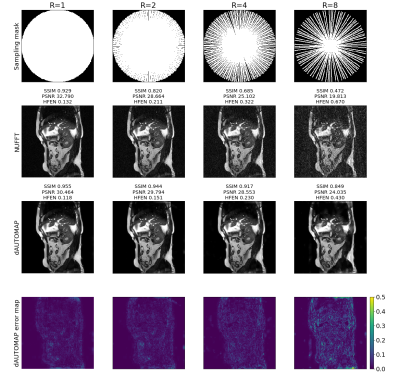
Recently, dAUTOMAP[1] has been presented as an improvement of AUTOMAP[2] that achieves a high-quality reconstruction with a low model parameter count by exploiting the fact that Fourier kernels are linearly separable. The novel decomposed transform layer (DT-layer) implements a one-dimensional learnable convolution kernel which can perform a 2D DFT by applying this layer twice, enabling the network to learn an optimal inverse transformation rooted in a Fourier basis for undersampled acquisitions.The dAUTOMAP model has been successfully demonstrated to reconstruct undersampled Cartesian acquisitions with high quality. Here we assess the performance of dAUTOMAP for non-Cartesian sampling strategies. We hypothesize that these acquisitions can be further undersampled than Cartesian acquisitions due to their benign undersampling artifacts. Reconstructing non-Cartesian acquisitions with dAUTOMAP requires that the k-space points are interpolated on a Cartesian grid because of the assumptions of the DT-layers. This creates additional artifacts because the gridding process operates with a finite-sized interpolation kernel. This introduces an undesired modulation in the reconstructed image, known as the roll-off effect[3]. This effect is shown in Figure 1.
In this work, we show that dAUTOMAP is able to reconstruct gridded, non-Cartesian acquisitions with high quality while resolving artifacts introduced by gridding step and retaining favorable properties of the respective sampling strategies.
Evaluation
We evaluated the dAUTOMAP reference implementation (https://github.com/js3611/dAUTOMAP) using ~26000 sagittal magnitude-only 2D cine images of the abdomen acquired in the clinic from 106 patients on a 1.5T MRI scanner (Ingenia, Philips, Best, the Netherlands) with a balanced steady-state free precession (bSSFP) sequence (TR/TE=2.8/1.4ms, FA=50o, resolution=1.42x1.42mm2, FOV=320x320mm2, matrix size=224x224, slice thickness=7mm) divided in a 75/25% train-test split on a patient-basis. K-space was obtained by adding artificial phase[2] to the image and computing the Fourier transform. This k-space was then retrospectively undersampled for several acceleration factors using the following sampling strategies:- Cartesian: As a benchmark we included a Cartesian undersampling scheme. In this randomly undersampled acquisition, the 17 central lines of k-space were always sampled, complemented with random peripheral k-space lines to match the acceleration factor.
- Radial: Undersampled k-space was created with a golden-angle radial trajectory. The number of spokes was selected such that R=1 would be sampled at the Nyquist rate, requiring $$$224 \cdot \pi/2=352$$$ spokes. For factors 2, 4, and 8 we used 176, 88 and 44 spokes, respectively.
- Spiral: A variable-density spiral[4] with 40 uniformly rotating interleaves was designed to be oversampled in the center of k-space and smoothly move to the edge of k-space. For R=2, 4, and 8 we used 20, 10, and 5 spirals, respectively.
Results & Discussion
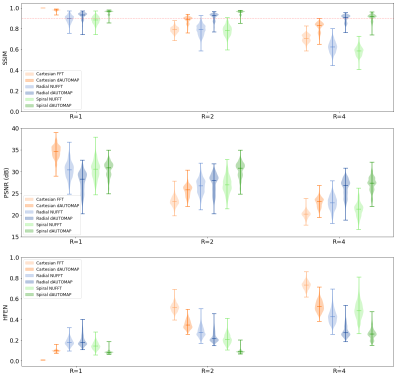
Quantitative results computed over the test set are shown in Figure 2. It can be noticed that only for R=1, Cartesian sampling outperforms non-Cartesian acquisitions. As the undersampling factor increases, reconstructing k-space with dAUTOMAP results in a higher performance than with conventional reconstructions. It can also be seen that non-Cartesian dAUTOMAP reconstructions show a higher performance than Cartesian reconstructions and show no roll-off effect. Compared to Cartesian dAUTOMAP reconstructions, non-Cartesian dAUTOMAP reconstructions have a 10% higher SSIM, 14-18% higher PSNR, and a 45-50% lower HFEN (Wilcoxon, p<0.001). Even for R=4, non-Cartesian dAUTOMAP reconstructions show an SSIM>0.9, indicating a slower decline in quality as the acceleration factor is increased.Typical reconstructions are shown in Figures 3, 4, and 5. It can be seen that Cartesian reconstructions are improved with dAUTOMAP but still show a high residual error for R=4 as visualized in the bottom row of Figure 3, computed as the absolute error of dAUTOMAP reconstructions w.r.t. the fully-sampled image. With radial and spiral trajectories, the residual error is lower and reconstructions are of higher quality. Even for R=8, radial dAUTOMAP reconstructions show fair quality and has similar quantitative metrics as Cartesian for R=4. With a spiral trajectory, dAUTOMAP is not able to reconstruct a high-quality image at R=8, which might be resolved by optimizing the trajectory parameters.
These results show that dAUTOMAP can reconstruct any trajectory after gridding and can even perform complex transforms inherent to the gridding operation such as roll-off correction.
Conclusion
We have demonstrated that dAUTOMAP is applicable to non-Cartesian acquistions after an initial gridding step and outperforms Cartesian reconstructions for undersampled acquisitions, especially for radial sampling. We have shown that dAUTOMAP is able to perform transformations beyond the (NU)FFT that are an inherent product of a gridding operation such as roll-off correction. Future work will focus on extending this framework to 3D acquisitions and reconstructing multi-coil data.Acknowledgements
This work is part of the research program HTSM with project number 15354, which is (partly) financed by the Netherlands Organization for Scientific Research (NWO). We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan Xp GPU used for prototyping this research.References
[1] Schlemper, Jo, et al. "dAUTOMAP: decomposing AUTOMAP to achieve scalability and enhance performance." arXiv preprint arXiv:1909.10995 (2019).
[2] Zhu, Bo, et al. "Image reconstruction by domain-transform manifold learning." Nature 555.7697 (2018): 487.
[3] Block, Kai Tobias. "Advanced methods for radial data sampling in magnetic resonance imaging." SUB University of Goettingen (2008).
[4] Lustig, Michael, Seung-Jean Kim, and John M. Pauly. "A fast method for designing time-optimal gradient waveforms for arbitrary k-space trajectories." IEEE transactions on medical imaging 27.6 (2008): 866-873.
[5] Lin, Jyh-Miin. "Python Non-Uniform Fast Fourier Transform (PyNUFFT): An Accelerated Non-Cartesian MRI Package on a Heterogeneous Platform (CPU/GPU)." Journal of Imaging 4.3 (2018): 51.
[6] Wang, Zhou, et al. "Image quality assessment: from error visibility to structural similarity." IEEE transactions on image processing 13.4 (2004): 600-612.
[7] Ravishankar, Saiprasad, and Yoram Bresler. "MR image reconstruction from highly undersampled k-space data by dictionary learning." IEEE transactions on medical imaging 30.5 (2010): 1028-1041.
Figures
Figure 1: Method overview. An example of our model setup for a radial trajectory. A non-Cartesian acquisition is density-compensated and gridded to a Cartesian grid. This gridded k-space serves as input for a dAUTOMAP model, which is trained for a specific sampling strategy and undersampling factor to reconstruct the corresponding fully-sampled image. A conventional Fourier reconstruction without roll-off correction would give severe “vignetting” artifacts as can be seen in the bottom reconstructed image.
Figure 2: Quantitative results. Quantitative
results using the SSIM, PSNR, and HFEN metrics respectively shows the performance characteristics of
dAUTOMAP reconstructions versus conventional (NU)FFT reconstructions on our test set. We can observe that in the fully-sampled case, non-Cartesian reconstruction shows good performance but as the undersampling factor increases, the performance of non-Cartesian dAUTOMAP reconstructions increases beyond Cartesian dAUTOMAP performance. The SSIM plot shows the 0.9 isoline.
Figure 3: Cartesian reconstruction. Top row shows the sampling masks for R=1, 2, and 4. For R=1, a near-perfect image is reconstructed, compared to the fully-sampled image, as shown in the conventional reconstruction for R=1. For R=2 dAUTOMAP shows a clear improvement and a fair image is reconstructed. For R=4, the artifact power becomes too great, even though dAUTOMAP clearly improves image quality w.r.t. a Fourier transform. The difference between the dAUTOMAP reconstruction and the fully-sampled image is shown in the bottom row.
Figure 4: Radial reconstruction. Top row shows sampling masks for R=1, 2, 4, and 8 using a golden-angle radial sampling strategy. Trajectories were created using 352, 176, 88 spokes, and 44 spokes, respectively. For R=1 a very high-quality image is reconstructed, even though some high-frequency components are missing. As the undersampling factor becomes higher, the image becomes smoother. Even for R=8 dAUTOMAP shows a fair reconstruction quality, even though some residual artifacts remain, as shown in the error map w.r.t. the fully-sampled image in the bottom row.
Figure 5: Spiral reconstruction. Top row shows the target image and the various sampling masks for R=1, 2, 4 and 8. The sampling mask was created from a variable-density spiral pattern with 40 interleaves. Sampling masks have 40, 20, 10 and 5 spirals, respectively. Notice that artifacts are completely removed in dAUTOMAP reconstructions (Row 3) for R=2. A good reconstruction is made for R=4, but dAUTOMAP fails to fully resolve the heavy artifacts at R=8. The dAUTOMAP error map (Row 4) compared to the fully-sampled target image show near-identical performance for R=1 and R=2.