3620
A Hybrid SENSE Reconstruction Combined with Deep Convolution Neural Network1School of Life Science and Technology, University of Electronic Science and Technology of China, chengdu, China, 2High Field Magnetic Resonance Brain Imaging Laboratory of Sichuan, Chengdu, China, 3Key Laboratory for Neuro Information, Ministry of Education, Chengdu, China
Synopsis
Recently parallel imaging reconstruction based on deep learning has made lots of progresses, however, there still exist several common challenges, i.e. generalization, transferability and robustness. On the contrary, SENSE reconstruction has been routinely used in clinical scans due to its high robustness and excellent image quality. A high-quality coil sensitivity map (HQCSM) is the key to achieve good SENSE reconstruction. We proposed a hybrid SENSE reconstruction frame, combining the SENSE reconstruction algorithm with a deep convolutional neural network to learn HQCSM from a few automatic calibration lines (ACS), which shows good generalization for different under-sampling ratio and enhanced robustness.
Introduction
Fast imaging has always been desired in Magnetic Resonance Imaging (MRI) with many benefits including shorter scan time, reduced motion artifact, increased spatial and temporal resolution and etc. Recently deep learning has seen dramatic progress and development at almost each step of the MRI workflows, from data acquisition to image post-processing and clinical diagnosis. Many efforts have been made to revolutionize the traditional fast imaging techniques with the powerful deep learning. However, most of the research works have been focused on building an end-to-end deep neural network to entirely replace the conventional imaging reconstruction algorithms. The common challenges of building such end-to-end models are the generalization, transferability and robustness. For example, if the deep learning model was trained with only a certain under-sampling ratio data, it generally doesn’t perform well for reconstruction at any different under-sampling ratios. On the other hand, traditional image-based parallel reconstruction, such as SENSE, has shown great robustness and has been vastly utilized in clinical scans demanding for fast imaging. In this work, we attempt to take fully advantage of the traditional SENSE as well as the power of deep learning technique to develop a hybrid SENSE reconstruction frame. In particular, we developed a deep convolutional neural network (CNN) to learn only a high-quality coil sensitivity map, which is the key for high quality SENSE reconstruction. As long as the high-quality coil sensitivity map is learned, it can be fed into the regular SENSE reconstruction algorithms. One big advantage of this method is that it may perform the same with actual parallel data acquisition at different under-sampling ratios. This has been demonstrated by an in-vivo experiment with actual acquired MRI data.Materials and Method
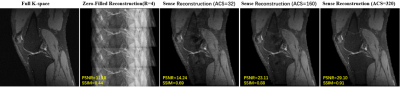
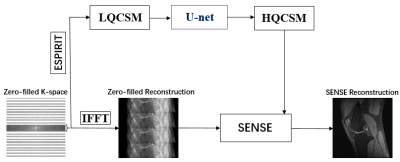
Materials: We have used the knee datasets of recently published variational network reconstruction method [3] and selected 4500 2-D multi-coil k-space raw data. The matrix size of a 2-D multi-coil k-space raw data is 320x320x8. The whole dataset was divided into three parts (training, validation, testing) by a ratio of 7:1:2. The raw data from http://old.mridata.org/undersampled/knees.Method: As shown in Figure 1, the imaging quality of SENSE reconstruction highly depends on the quality of coil sensitivity map. Higher quality coil sensitivity map requires more automatic calibration lines (ACS) which means more scan time. Here we attempt to develop a deep CNN to achieve a high-quality coil sensitivity map with less ACS. In particular, we transform low quality coil sensitivity maps (LQCSM) generated by ACS=32 to high quality coil sensitivity maps (HQCSM) generated by ACS=320 via U-net convolutional neural network [5] and perform the conventional SENSE reconstruction with the “deep learned” HQCSM (Figure 2). Since the U-net convolutional neural network works only on real-valued parameters, the complex data of LQCSM are divided into real and imaginary parts and then concatenated as sixteen-channel inputs in the channel direction. In order to improve the generalization and robustness of the model, data augmentation (flip, translation, scale) was implemented during training. The network was trained in TensorFlow with the following parameters: loss minimization performed using ADAM [6] optimizer with an update rate of 0.001, batch size = 8, loss = mean square error (MSE).
Results
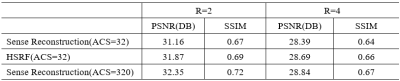
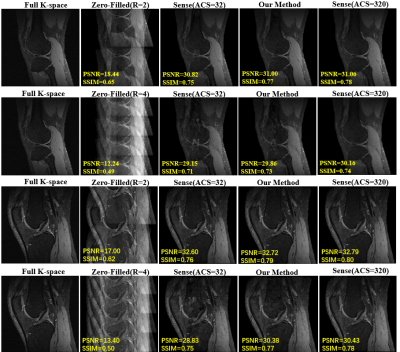
Table 1 compares the image reconstruction results on the testing dataset between our proposed method and conventional SENSE with coil sensitivity map calculated by different number of ACS (ACS=32 and ACS=320) Figure 3 shows an in-vivo experiment with actual acquired data. The actual k-space data was obtained by interlaced scanning with R=0, R=2 and R=4 from a GE 3.0T MR scanner. We keep ACS=32 during the scan. The reconstruction pipeline of our method consists of the following three steps: 1) the LQCSM was computed by ESPIRIT with ACS=32; 2) the HQCSM was obtained via trained U-net, taking LQCSM as inputs; 3) MR images was reconstructed from the aliasing MR images (R=2, R=4) using the conventional SENSE algorithm but with the “deep-learned” HQCSM from step 2. It can be observed that SENSE (ACS=model) reconstruction has better image quality than the conventional SENSE (ACS=32) and almost similar reconstruction quality with conventional SENSE (ACS=320).Conclusion
A hybrid SENSE reconstruction frame was proposed with respect to the existing challenges for deep learning based parallel imaging reconstruction approaches, i.e. generalization, transferability and robustness. Comparing to the end-to-end deep learning reconstruction method, our hybrid reconstruction scheme possesses of better generalization, transferability and robustness. An in-vivo experiment based on real acquired data demonstrates that our method has good generalization for different under-sampling ratio and enhanced robustness.Acknowledgements
References
1. Pruessmann, K. P., Weiger, M., Scheidegger, M. B., Boesiger, P., et al., Sense: sensitivity encoding for fast mri," Magnetic resonance in medicine 42(5), 952{962 (1999).
2. Griswold, M. A., Jakob, P. M., Heidemann, R. M., Nittka, M., Jellus, V., Wang, J., Kiefer, B., and Haase, A., Generalized autocalibrating partially parallel acquisitions (grappa)," Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 47(6), 1202{1210(2002).
3. Hammernik, K., Klatzer, T., Kobler, E., Recht, M. P., Sodickson, D. K., Pock, T., and Knoll, F., Learning a variational network for reconstruction of accelerated mri data," Magnetic resonance in medicine 79(6), 3055{3071 (2018).
4. Uecker, M., Lai, P., Murphy, M. J., Virtue, P., Elad, M., Pauly, J. M., Vasanawala, S. S., and Lustig, M., Espiritan eigenvalue approach to autocalibrating parallel mri: where sense meets grappa," Magnetic resonance in medicine 71(3), 990{1001 (2014).
5. Ronneberger, O., Fischer, P., and Brox, T., \U-net: Convolutional networks for biomedical image segmentation," in [International Conference on Medical image computing and computer-assisted intervention], 234{241, Springer (2015).
6. Kingma, D. P. and Ba, J., Adam: A method for stochastic optimization," arXiv preprint arXiv:1412.6980 (2014).
Figures